算法很美(二)
二、查找与排序(上)
目标:
①对递归建立起感觉
②学会评估算法性能
③大致预估程序执行时间
1、简单递归
递归——自己调用自己,先来个最简单例子
public class Recursive {
public static void main(String[] args) {
f(10);
}
//千万注意不要死循环
static void f(int i) {
if(i==0)
return;
//调用自身
f(i-1);
}
}
然后先来一些简单案例
牢记在心三步骤:
① 找重复:对原问题的重复,规模更小——父问题转求解子问题,找到一种划分方法、递推公式或者等价转换
② 找变化:变化的量通常作为参数,适当时要自行添加参数
③ 找边界:出口,就是条件,不能死循环下去
求阶乘
/*
*求n的阶乘
*找重复:n*(n-1),n-1的阶乘是对原问题的重复,只是规模更小——子问题
*找变化:变化的量应该作为参数 n
*找边界:出口,就是条件,不能死循环下去
*/
public class JieCheng {
public static void main(String[] args) {
System.out.println(func(10));
}
public static int func(int n) {
//写终止条件
if (n==1)
return 1;
return n*func(n-1);
}
}
打印i-j
/*
*打印i-j
* 找重复:i不断增加靠向j--->i+1
* 找变化:i不断增加
* 找出口:终止条件--->i>j则停止
*/
public class Print {
public static void main(String[] args) {
func(1,10);
}
public static void func(int i,int j) {
if (i>j)
return;
System.out.print(i+" ");
func(i+1,j);
}
}
对arr所有元素求和
/*
* 对arr所有元素求和
* 重复:数组里我们要开始的那块,假设为begin
* 变化:数组长度、起点在变化,所以必须要加参数就是begin
* 出口:当begin==arr.length-1
*/
public class ShuZu {
public static void main(String[] args) {
int[] arr = {1,2,3,4,5,6,7,8,9,10};
//从索引0处开始求和
System.out.println(fun(arr,0));
}
public static int fun(int[] arr, int begin) {
if (begin==arr.length-1) {
return arr[begin];
}
return arr[begin]+fun(arr,begin+1);
}
}
反转
/*
* 反转
* 重复:[a,b,c,d]-->d reverse[a,b,c]-->c reverse[a,b]-->b reverse[a]-->[d,c,b,a]
* 这一反转过程就在不断重复
* 变化:应该是最后的那个数字,我们设置其索引为end
* 出口:本例中end为3,当其反转成为0时,结束即可
*/
public class Reverse {
public static void main(String[] args) {
System.out.println(fun("abcd",3));
}
public static String fun(String src,int end) {
if (end==0) {
return ""+src.charAt(0);
}
return src.charAt(end)+fun(src,end-1);
}
}
总结:切蛋糕,在重复中找变化,在变化中找重复。
一些特殊的递归,很常见的。
经典Fibonacci
/*
* 分解方法: 1、直接量+小规模子问题
* 2、多个小规模子问题
* 重复:n =(n-1)+(n-2)
* 变化:先纵在横(此题可以看成一个树模型)
* 出口:当n=1和n=2并没有变化,此时为出口
*/
public class Fibonacci {
public static void main(String[] args) {
// 1 1 2 3 5
// f(n) = f(n-1)+f(n-2)
}
public static int func(int n) {
if (n==1 ||n==2)
return 1;
return func(n-1)+func(n-2);
}
}
解最大公约数
/*
* 最大公约数
* 重复:m%n=0 则n为GCD 若m%n=k ,再n%k=0 则k为GCD
* 变化: f(m,n)--->f(n,m%n)
* 出口:余数为0,即n==0,则返回的m为GCD
*/
public class DCD {
public static void main(String[] args) {
System.out.println(func(10,5));
//输出5
}
public static int func(int m,int n) {
if (n==0)
return m;
return func(n,m%n);
}
}
汉诺塔
先通过图示来进行简单了解
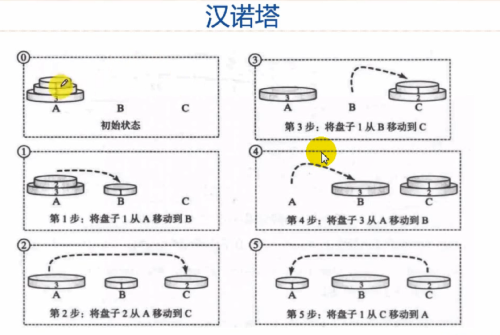
/*
* 假设N个盘子现都在A上,将1~N-1个盘子移到C上,将盘子N移到B上,此时A为空,便可依次重复
* 等价一下:
* 1、1~N-1从A移到C,B为辅助
* 2、N从A移到B
* 3、1~N-1从C移到B,A为辅助
*/
public class HanNuoTa {
public static void main(String[] args) {
Move(3,"A","B","C");
}
public static void Move(int N,String from,String to,String help) {
if (N==1) {
System.out.println("move "+N+" from"+from+" to "+to);
}else {
//把N-1个盘子移到辅助空间上
Move(N-1,from,help,to);
//N达到target
System.out.println("move "+N+" from"+from+" to "+to);
//N-1从辅助空间回到源空间上
Move(N-1,help,to,from);
}
}
}
2、二分查找递归
什么是二分查找?很简单,我让你猜个数1-100,首先取50,我说大了,就不用去猜50-100区间了,直接在1-49里面再猜就好了。
那么二分查找就等价于三个子问题:
- 左边找(递归)
- 中间比
- 右边找(递归)
左右两边区域查找直选其一即可。
//写一下二分查找递归的算法
private static int binarySearch(int[] arr,int low ,int high,int key) { //low起点,high终点
if (low>high)
return -1; //出口
int mid = low+((high-low)>>1); //移位更高效
int midVal = arr[mid];
//子问题
if (midVal<key) {
return binarySearch(arr,mid+1,high,key);
}
else if (midVal>key) {
return binarySearch(arr,low,high-1,key);
}
else
return mid; //key found
}
3、希尔排序
也是一种插入排序,是简单插入排序经过改进后一个更高效的排序,也称缩小增量排序,复杂度在O(nlgn)约是n1.3-O(n2)。
确定一个增量序列,用增量分组,组内进行排序,直到最后排序成功。
画了一个草图,不要介意:
对 9 8 7 6 5 4 3 2 1进行排序

书写一下代码:
import java.util.Arrays;
/*
* 希尔排序
* 在原数组arr中,interval=9/2=4,间隔为4,则[9,5,1]为一起排序
*/
public class ShellSort {
public static void main(String[] args) {
int[] arr ={9,8,7,6,5,4,3,2,1};
fun(arr);
System.out.println(Arrays.toString(arr));
}
public static void fun(int[] arr) {
//不断缩小增量
for (int interval=arr.length/2; interval>0; interval=interval/2) {
//增量为interval的插入排序
for (int i=interval;i<arr.length;i++) {
int target = arr[i];
int j = i-interval; //j是比较元素
while (j>-1&&target<arr[j]) { //不断往自己的组插入
arr[j+interval] = arr[j];
j -= interval;
}
arr[j+interval] = target;
}
/* 增量为1的插入排序
for (int i=1;i<arr.length;i++) {
int target = arr[i];
int j = i-1;
while (j>-1&&target<arr[j]) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = target;
}*/
}
}
}
4、评估算法性能
评估算法性能,主要评估问题的输入规模n与元素的访问次数f(n)的关系,这里我们就要说到时间复杂度了
时间复杂度是衡量算法好坏的重要指标之一。时间复杂度反映的是不确定性样本量的增长对于算法操作所需时间的 影响程度,与算法操作是否涉及到样本量以及涉及了几次直接相关,如遍历数组时时间复杂度为数组长度n(对应 时间复杂度为 O(n) ),而对数据的元操作(如加减乘除与或非等)、逻辑操作(如if判断)等都属于常数时间内 的操作(对应时间复杂度 O(1) )。
在化简某算法时间复杂度表达式时需遵循以下规则:
①对于同一样本量,可省去低阶次数项,仅保留高阶次数项,如 O(n^2)+O(n) 可化简为 O(n^2) , O(n)+O(1) 可化简为 O(n)②可省去样本量前的常量系数,如 O(2n) 可化简为 O(n) , O(8) 可化简为 O(1)
③对于不同的不确定性样本量,不能按照上述两个规则进行化简,要根据实际样本量的大小分析表达式增量。 如 O(logm)+O(n^2) 不能化简为 O(n^2) 或 O(logm) 。而要视m、n两者之间的差距来化简,比如m>>n时 可以化简为 O(logm) ,因为表达式增量是由样本量决定的。
简单来几个例子评估一下:
O(n)
for(int i=1; i<n; i++) {
k += 5;
}
//时间复杂度O(n)
O(n^2)
for(int i=1; i<n; i++) {
for(int j=1; j<i; j++) { //n*n
k = k+i+j; //n*n*t ,t可忽略不计
}
}
//时间复杂度O(n)
/*
* 写个好理解的公式
* T(n)=c+2c+3c+...+nc
* =cn(n+1)/2
* =(c/2)n^2+(c/2)n
* =O(n^2)
*/
O(log2 n)
int count = 1;
while(count<n) {
count = count*2;
}
//对数复杂度,时间复杂度O(log2 n)
这里其实是以指数形式增长,举个例子n=5
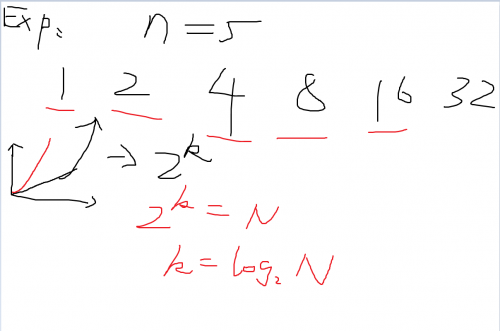
5、常见函数复杂度
直接看直观效果图:

常用的时间复杂度按照耗费的时间从小到大依次是:
O(1)<O(log n)<O(n)<O(n log n)<O(n²)<O(n³)<O(2ⁿ)<O(n!)
6、对比顺序查找和二分查找
顺序查找:O(logn)
二分查找:O(lgn)
看一下代码:
public class Compare {
private static int search(int[] arr,int key) {
for (int i=0;i<arr.length;i++) {
if (arr[i] == key) {
return i;
}
}
return -1;
}
private static int binarySearch(int arr[],int low,int high,int key) {
if (low>high) {
return -1;
}
int mid = low+((high-low)>>1);
int midVal = arr[mid];
if (midVal<key) {
return binarySearch(arr,mid+1,high,key);
}
else if (midVal>key) {
return binarySearch(arr,low,high-1,key);
}
else
return mid;
}
public static void main(String[] args) {
int[] x = new int[10000*1000];
for (int i=0;i<x.length;i++) {
x[i] = i+1;
}
int target = 10000*10000;
long now = System.currentTimeMillis();
int index =binarySearch(x,0,x.length-1,target);
System.out.println("二分查找时间:"+(System.currentTimeMillis()-now)+"ms");
System.out.println(target+"所在位置为:"+index);
now = System.currentTimeMillis();
index = search(x,target);
System.out.println("顺序查找时间:"+(System.currentTimeMillis()-now)+"ms");
}
}
//out:
//二分查找时间:0ms
//100000000所在位置为:-1
//顺序查找时间:7ms
由此可见,二分查找比顺序查找快了很多。
7、冒泡、插入、选择排序分析
画图来认识一下这三种排序方法:
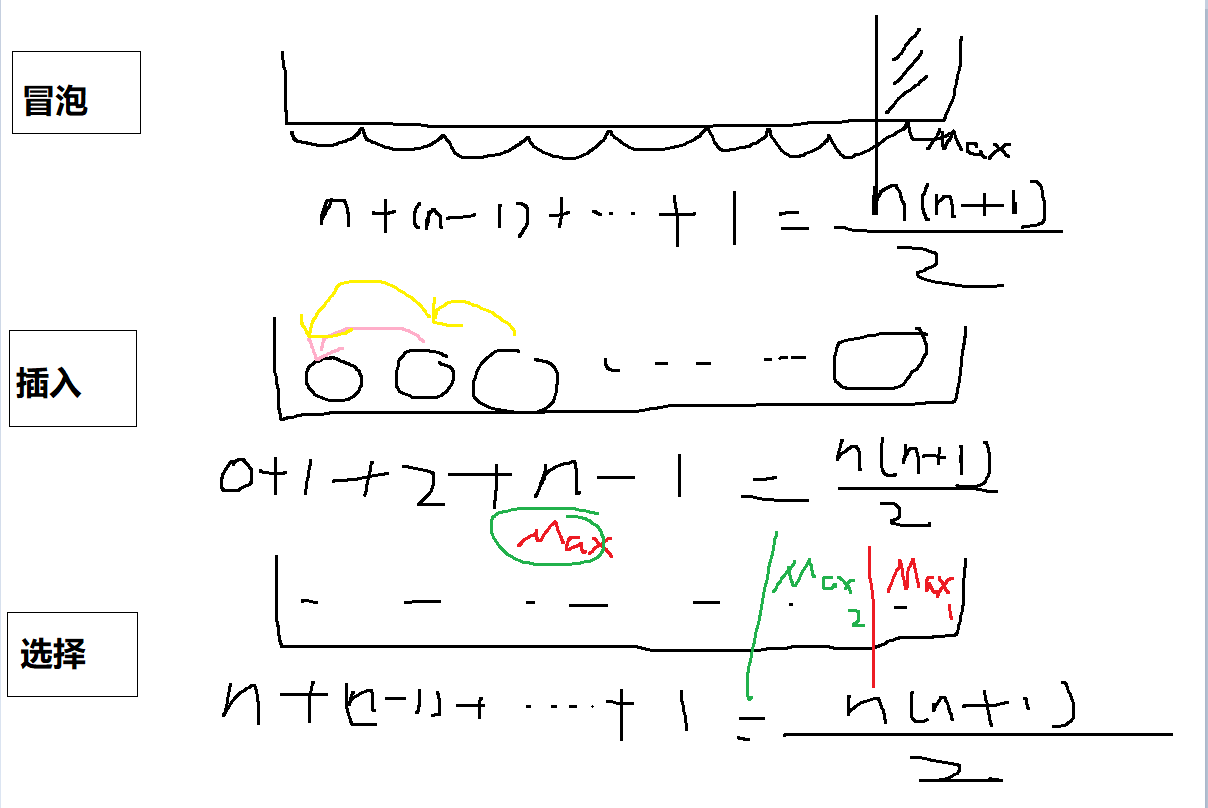
可见它们的次数都是n(n+1)/2,所以时间复杂度均为O(n^2)
冒泡排序:
public class BubbleSort {
public static int[] bubbleSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length - i -1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
return arr;
}
public static void main(String[] args) {
int[] arr = {2,5,1,3,8,5,7,4,3};
int[] res = bubbleSort(arr);
for (int item: res
) {
System.out.println(item+" ");
}
}
}
插入排序:
import java.util.Arrays;
public class InsertSort {
public static void insertionSort(int[] unsorted){
for (int i = 1; i < unsorted.length; i++) {
if (unsorted[i - 1] > unsorted[i]) {
int temp = unsorted[i];
int j;
for (j = i - 1; j >= 0 && unsorted[j] > temp; j--) {
unsorted[j + 1] = unsorted[j];
}
unsorted[j + 1] = temp;
}
}
}
public static void main(String[] args) {
int[] arr = {2,5,1,3,8,5,7,4,3};
insertionSort(arr);
System.out.println(Arrays.toString(arr));
}
}
选择排序:
public class SelectSort {
public static void main(String[] args) {
int[] array = {2,5,1,3,8,5,7,4,3};
System.out.println("原数组:");
for (int i : array) {
System.out.print(i+" ");
}
System.out.println();
selectSort(array);
System.out.println("排序后:");
for (int i : array) {
System.out.print(i+" ");
}
}
public static void selectSort(int[] arr){
for(int i = 0; i < arr.length-1; i++){
int min = i;
for(int j = i+1; j <arr.length ;j++){
if(arr[j]<arr[min]){
min = j;
}
}
if(min!=i){
swap(arr, i, min);
}
}
}
//完成数组两元素间交换
public static void swap(int[] arr,int a,int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
记一个2的幂表:
| 2的幂 | 准确值(X) | 近似值 | X字节转换成MB、GB等 |
|---|---|---|---|
| 7 | 128 | ||
| 8 | 256 | ||
| 10 | 1 024 | 一千 | 1K |
| 16 | 65 536 | 64K | |
| 20 | 1 048 576 | 一百万 | 1MB |
| 30 | 1 073 741 824 | 十亿 | 1GB |
| 32 | 4 294 967 296 | 4GB | |
| 40 | 1 099 511 627 776 | 一万亿(trillion) | 1TB |
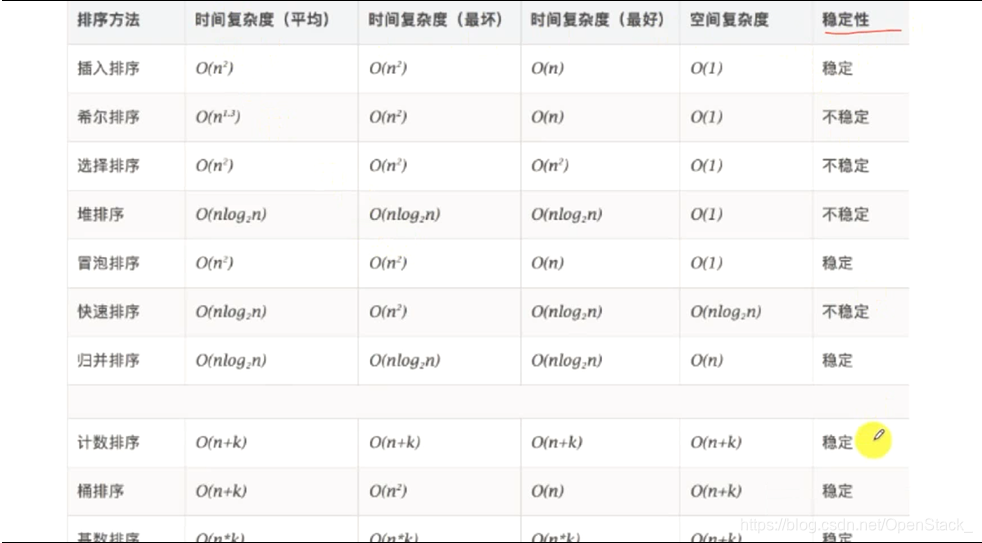
8、排序算法的稳定性
稳定:如果a原本在b前面,而a=b,排序之后a仍在b的前面。
不稳定:如果a原本在b前面,而a=b,排序之后a可能在b的后面。
9、递归小白上楼梯
题目:小白正在上楼梯,楼梯有n阶台阶,小白一次可以上1阶、2阶、3阶,实现一个方法,计算小白有多少种方法可以走完。
思路:
可以当成消消乐来看待,重复消去的实现为f(n-1)+f(n-2)+f(n-3),出口实现即在n为0、1、2的情况下只会有各自一种方法。
实现:
import java.util.Scanner;
public class PaLouTi {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (true) {
int n = sc.nextInt(); //n为阶梯数
int res = fun(n);
System.out.println(res);
}
}
private static int fun(int n) {
if (n==0) return 1;//若此处return 0,则假如n=3,(1,2)和(2,1)为一种情况,所有的两个数的情况都会看为重复-1
if (n==1) return 1;
if (n==2) return 2;
return fun(n-1)+fun(n-2)+fun(n-3);
}
}
10、旋转数组的最小数字
题目:把一个数组最开始的若干元素搬到数组末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。如:数组{3,4,5,1,2}为{1,2,3,4,5}的旋转,min=1。
思路:
强调原数组为递增有序的,用二分法的思想来做,中间切,抽取出无序的一段,如上:{5,1,2}。递归,抽取出{5,1},则end==min。
实现:
package BlueBridge.Chapter2;
public class XuanZhuanShuZu {
static int min(int[] arr) {
int begin = 0;
int end = arr.length-1;
//考虑没有旋转这种特殊的旋转,{1,2,3,4,5}->1
if (arr[begin]<arr[end]) {
return arr[begin];
}
//begin和end指向相邻元素退出
while (begin+1<end) {
int mid = begin+((end-begin)>>1);
//要么左侧有序,要么右侧有序
if (arr[mid]>=arr[begin]) {
//有序
begin = mid;
//无序
}else {
end = mid;
}
}
return arr[end]; //输出最小的那个数字
}
public static void main(String[] args) {
int[] arr = {5,1,2,3,4};
int res = min(arr);
System.out.println(res);
}
}
缺漏:
若果数组{1,0,1,1,1},像这样分后仍会有begin=mid=end,如果有这种情况,只能通过扫描法获取。
11、在有空字符串的有序字符串数组中查找
题目:有个排序后的字符串数组,其中散布着一些空字符串,编写一个方法,找出给定字符串(肯定不是空字符串)的索引
思路:
仍然使用二分法的思想来做,套路都相同
实现:
public class FindIndex {
public static void main(String[] args) {
String[] arr = {"a","","ac","","ad","b","","ba"};
int res = indexOf(arr,"b"); //5
System.out.println(res);
}
private static int indexOf(String[] arr,String p) {
int begin = 0;
int end = arr.length-1;
while (begin<=end) {
int indexOfMid = begin+((end-begin)>>1);
while (arr[indexOfMid].equals("")){
indexOfMid++;
//be careful
if (indexOfMid>end)
return -1;
}
if (arr[indexOfMid].compareTo(p)>0) {
end = indexOfMid-1;
}else if (arr[indexOfMid].compareTo(p)<0) {
begin =indexOfMid+1;
}else {
return indexOfMid;
}
}
return -1;
}
}
补充:
有小伙伴看不懂 >>1的操作,其实在Java中有三种移位运算符:
<< : 左移运算符,num << 1,相当于num乘以2
>> : 右移运算符,num >> 1,相当于num除以2
>>> : 无符号右移,忽略符号位,空位都以0补齐
12、最长连续递增子序列(部分有序)
题目:(1,9,2,5,7,3,4,6,8,0)中最长的递增子序列为(3,4,6,8)
思路:
做一个指针,开始扫描,扫描过程中,遇到后一个数字小于前一个数则归1,重新开始计算,得出最大长度即可
实现:
public class LongestZiChuanLength {
public static void main(String[] args) {
int[] res= {1,9,2,5,7,3,4,6,8,0}; // 4
System.out.println(getMaxlength(res));
}
private static int getMaxlength(int[] A) {
int size=A.length;
if (size <= 0)
return 0;
int res = 1;
int current = 1;
for (int i = 1; i < size; i++) {
if (A[i] > A[i - 1]) {
current++;
} else {
if (current > res) {
res = current;
}
current = 1;
}
}
return res;
}
}

 这一章学习查找和排序,当然我们先从有趣的递归开始
这一章学习查找和排序,当然我们先从有趣的递归开始

