leetcode 115. 不同的子序列

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

题目数据保证答案符合 32 位带符号整数范围。

 

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit
示例 2：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下图所示, 有 5 种可以从 s 中得到 "bag" 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag
 

提示：

0 <= s.length, t.length <= 1000
s 和 t 由英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/distinct-subsequences
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

采用动态规划，创建二维数组arr[i][j] 分别表示从后往前数，以s中倒数第i个开头的字符串 中包含多少个在t中倒数第j个字符为开头的字符串的子序列。
以babgbag 和 bag为例子。
可以得到二维数组如下，最后求和即为答案。

 

 

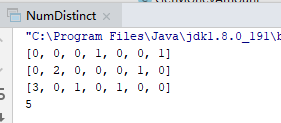
    public int numDistinct(String s, String t) {
        int a = s.length();
        int b = t.length();
        if (a == 0 || b == 0) {
            return 0;
        }
        char[] as = s.toCharArray();
        char[] bs = t.toCharArray();
        int[][] arr = new int[b + 1][a];
        int sum = 1;
        for (int i = b - 1; i >= 0; i--) {
            char c = bs[i];
            int[] item = arr[i];
            int[] last = arr[i + 1];
            for (int j = a - 1; j >= 0; j--) {
                if (c == as[j]) {
                    item[j] = sum;
                }
                sum += last[j];
            }
            sum = 0;
        }
        int[] item = arr[0];
        for (int i : item) {
            sum += i;
        }
        return sum;
    }

 

可以优化为一维数组来解题，代码如下。

    public int numDistinct(String s, String t) {
        int a = s.length();
        int b = t.length();
        if (a == 0 || b == 0) {
            return 0;
        }
        char[] as = s.toCharArray();
        char[] bs = t.toCharArray();
        int[] arr = new int[a];
        int sum = 1;
        for (int i = b - 1; i >= 0; i--) {
            char c = bs[i];
            for (int j = a - 1; j >= 0; j--) {
                int n = arr[j];
                arr[j] = c == as[j] ? sum : 0;
                sum += n;
            }
            sum = 0;
        }
        for (int i : arr) {
            sum += i;
        }
        return sum;
    }