leetcode 576. 出界的路径数

给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你 最多 可以移动 maxMove 次球。

给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余 后的结果。

 

示例 1：

输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
输出：6
示例 2：

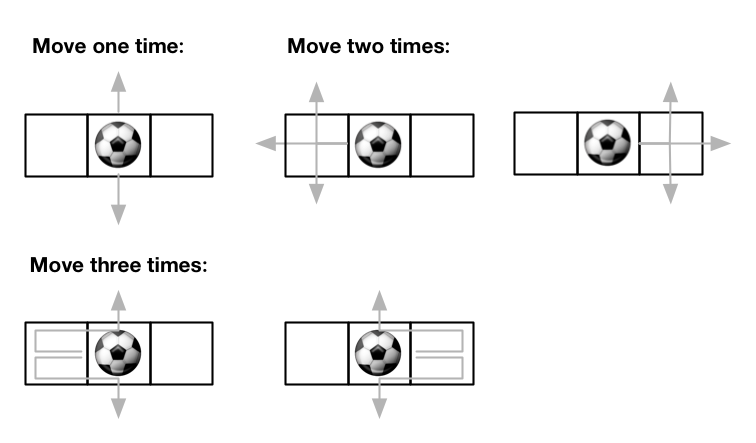
输入：m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
输出：12
 

提示：

1 <= m, n <= 50
0 <= maxMove <= 50
0 <= startRow < m
0 <= startColumn < n

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/out-of-boundary-paths
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

数组存储每个坐标到达边界的步数。

1：创建一个三维数组arr[i][j][k]

i:横坐标，j:纵坐标，k:到达边界所用的步数，arr[i][j][k] 表示坐标（i, j）经过k 步到达边界的所有路径数量。

2：方程为：

sum += i == 0 ? 1 : arr[i - 1][j][k - 1];

sum += j == 0 ? 1 : arr[i][j - 1][k - 1];

sum += i == m - 1 ? 1 : arr[i + 1][j][k - 1];

sum += j == n - 1 ? 1 : arr[i][j + 1][k - 1];

arr[i][j][k] = sum % 1000000007 ;

坐标（i, j）经过k 步到达边界的所有路径数量 = 四周 k - 1步到达边界是数量。

 

    public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
        long[][][] arr = new long[m][n][maxMove + 1];
        for (int k = 1; k <= maxMove; k++) {
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    long sum = 0;
                    sum += i == 0 ? 1 : arr[i - 1][j][k - 1];
                    sum += j == 0 ? 1 : arr[i][j - 1][k - 1];
                    sum += i == m - 1 ? 1 : arr[i + 1][j][k - 1];
                    sum += j == n - 1 ? 1 : arr[i][j + 1][k - 1];
                    arr[i][j][k] = sum % 1000000007 ;
                }
            }
        }
        return (int) (arr[startRow][startColumn][maxMove] % 1000000007);
    }