leetcode 987. 二叉树的垂序遍历

给你二叉树的根结点 root ，请你设计算法计算二叉树的 垂序遍历 序列。

对位于 (row, col) 的每个结点而言，其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。

二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束，按列索引每一列上的所有结点，形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点，则按结点的值从小到大进行排序。

返回二叉树的 垂序遍历 序列。

 

示例 1：

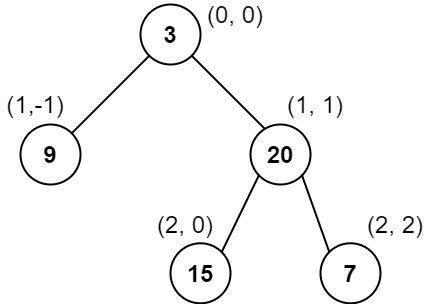
输入：root = [3,9,20,null,null,15,7]
输出：[[9],[3,15],[20],[7]]
解释：
列 -1 ：只有结点 9 在此列中。
列 0 ：只有结点 3 和 15 在此列中，按从上到下顺序。
列 1 ：只有结点 20 在此列中。
列 2 ：只有结点 7 在此列中。
示例 2：

输入：root = [1,2,3,4,5,6,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
列 -2 ：只有结点 4 在此列中。
列 -1 ：只有结点 2 在此列中。
列 0 ：结点 1 、5 和 6 都在此列中。
1 在上面，所以它出现在前面。
5 和 6 位置都是 (2, 0) ，所以按值从小到大排序，5 在 6 的前面。
列 1 ：只有结点 3 在此列中。
列 2 ：只有结点 7 在此列中。
示例 3：

输入：root = [1,2,3,4,6,5,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
这个示例实际上与示例 2 完全相同，只是结点 5 和 6 在树中的位置发生了交换。
因为 5 和 6 的位置仍然相同，所以答案保持不变，仍然按值从小到大排序。
 

提示：

树中结点数目总数在范围 [1, 1000] 内
0 <= Node.val <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/vertical-order-traversal-of-a-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

1：前序遍历二叉树。

2：用一个Map<Integer, Map<Integer, PriorityQueue<Integer>>> map 来记录各个节点。 其中key1 为横坐标，key2为纵坐标， value 为横纵坐标相同的节点值的集合。

3：遍历完二叉树，即可得到map。

4：遍历map，组装成所求的结果集。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> verticalTraversal(TreeNode root) {
        Map<Integer, Map<Integer, PriorityQueue<Integer>>> map = new HashMap<>();
        find(root, map, 0, 0);
        Set<Integer> set = map.keySet();
        int min = 0;
        int max = 0;
        for (Integer value : set) {
            min = Math.min(min, value);
            max = Math.max(max, value);
        }
        List<List<Integer>> all = new ArrayList<>(map.size());
        for (int i = min; i <= max; i++) {
            Map<Integer, PriorityQueue<Integer>> itemMap = map.get(i);
            List<Integer> list = new ArrayList<>();
            for (Map.Entry<Integer, PriorityQueue<Integer>> entry : itemMap.entrySet()) {
                PriorityQueue<Integer> value = entry.getValue();
                while (!value.isEmpty()) {
                    list.add(value.poll());
                }
            }
            all.add(list);
        }
        return all;
    }

    private void find (TreeNode node, Map<Integer, Map<Integer, PriorityQueue<Integer>>> map, int index, int d) {
        if (node == null) {
            return;
        }
        PriorityQueue<Integer> list = map.computeIfAbsent(index, v -> new TreeMap<>()).computeIfAbsent(d, v -> new PriorityQueue<>());
        list.add(node.val);
        find(node.left, map, index - 1, d + 1);
        find(node.right, map, index + 1, d + 1);
    }
}