leetcode 863. 二叉树中所有距离为 K 的结点

给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。

返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

 

示例 1：

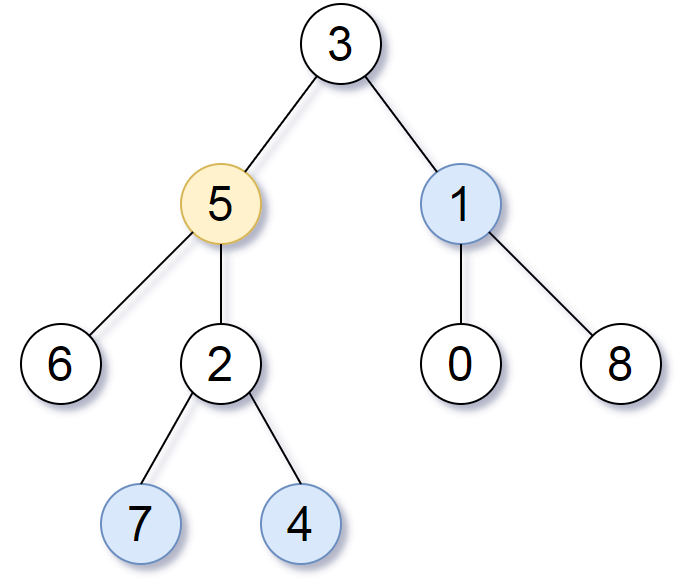
输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出：[7,4,1]
解释：
所求结点为与目标结点（值为 5）距离为 2 的结点，
值分别为 7，4，以及 1

 

注意，输入的 "root" 和 "target" 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。
 

提示：

给定的树是非空的。
树上的每个结点都具有唯一的值 0 <= node.val <= 500 。
目标结点 target 是树上的结点。
0 <= K <= 1000.
通过次数31,424提交次数52,194

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/all-nodes-distance-k-in-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

1：首先遍历二叉树，找到目标值，并且用一个list来记录从根节点到目标节点的路径。

2：从后往前遍历list， 每一个节点到目标节点的距离都是其坐标的差值。

3：list的长度为size, 所以本地可以转换为：

寻找到list.get（size - 1） 节点 距离为 k的其子节点。

寻找到list.get（size - 2） 节点 距离为 k - 1的其子节点（不能包含 list.get（size - 1） 节点发分支）。

寻找到list.get（size - 3） 节点 距离为 k - 2的其子节点（不能包含 list.get（size - 2） 节点发分支）。

以此类推，从后往前遍历list，每次都寻找的距离k--。直到k 为0，或者到根节点。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        List<TreeNode> list = new ArrayList<>();
        List<Integer> values = new ArrayList<>();
        find(root, target, list);
        int size = list.size() - 1;
        TreeNode node;
        addValues(list.get(size), values, 0, k);
        int count = 2;
        for (int i = size; i > 0; i--) {
            if (count - 1 == k) {
                values.add(list.get(i - 1).val);
                break;
            }
            node = list.get(i);
            TreeNode treeNode = list.get(i - 1);
            if (treeNode.left == null || treeNode.right == null) {
                count++;
                continue;
            }
            if (node.val == treeNode.left.val) {
                addValues(treeNode.right, values, count++, k);
            } else {
                addValues(treeNode.left, values, count++, k);
            }
        }
        return values;
    }

    private void addValues(TreeNode node, List<Integer> values, int n, int k) {
        if (node == null) {
            return;
        }
        if (n == k) {
            values.add(node.val);
            return;
        }
        addValues(node.left, values, n + 1, k);
        addValues(node.right, values, n + 1, k);
    }


    private boolean find(TreeNode node, TreeNode target, List<TreeNode> list) {
        if (node == null) {
            return false;
        }
        list.add(node);
        if (target.val == node.val) {
            return true;
        }
        boolean b = find(node.left, target, list);
        if (b) {
            return b;
        }
        b = find(node.right, target, list);
        if (!b) {
            list.remove(list.size() - 1);
        }
        return b;
    }
}