leetcode 1008. 前序遍历构造二叉搜索树

返回与给定前序遍历 preorder 相匹配的二叉搜索树（binary search tree）的根结点。

(回想一下，二叉搜索树是二叉树的一种，其每个节点都满足以下规则，对于 node.left 的任何后代，值总 < node.val，而 node.right 的任何后代，值总 > node.val。此外，前序遍历首先显示节点 node 的值，然后遍历 node.left，接着遍历 node.right。）

题目保证，对于给定的测试用例，总能找到满足要求的二叉搜索树。

 

示例：

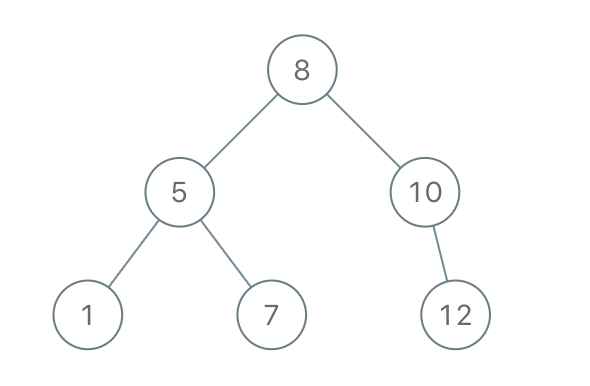
输入：[8,5,1,7,10,12]
输出：[8,5,10,1,7,null,12]

 

提示：

1 <= preorder.length <= 100
1 <= preorder[i] <= 10^8
preorder 中的值互不相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/construct-binary-search-tree-from-preorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

因为是二叉搜索树，所以数组排序之后，就是中序遍历，可以转化为根据前序和中序，构造二叉树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        int[] inorder = Arrays.copyOf(preorder, preorder.length);
        Arrays.sort(inorder);
        return buildTree(preorder, inorder);
    }
    
    private TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || preorder.length == 0) {
            return null;
        }
        int length = preorder.length - 1;
        TreeNode node = new TreeNode(preorder[0]);
        find(preorder, inorder, node, 0, length, 0, length);
        return node;
    }

    private void find(int[] preorder, int[] inorder, TreeNode node, int st, int end, int st2, int end2) {
        if (st > end) {
            return;
        }
        int value = preorder[st];
        int split = st2;
        for (int j = st2; j <= end2; j++) {
            if (inorder[j] == value) {
                split = j;
                break;
            }
        }
        int leftLength = split - st2;
        if (leftLength != 0) {
            TreeNode l = new TreeNode(preorder[st + 1]);
            node.left = l;
            find(preorder, inorder, l, st + 1, st + leftLength, st2, split - 1);
        }
        if (split != end2) {
            TreeNode r = new TreeNode(preorder[st + 1 + leftLength]);
            node.right = r;
            find(preorder, inorder, r, st + 1 + leftLength, end, split + 1, end2);
        }
    }
}