leetcode 1457. 二叉树中的伪回文路径

给你一棵二叉树，每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的，当它满足：路径经过的所有节点值的排列中，存在一个回文序列。

请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。

 

示例 1：

 

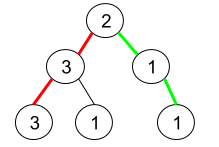
输入：root = [2,3,1,3,1,null,1]
输出：2
解释：上图为给定的二叉树。总共有 3 条从根到叶子的路径：红色路径 [2,3,3] ，绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中，只有红色和绿色的路径是伪回文路径，因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ，绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
示例 2：

 

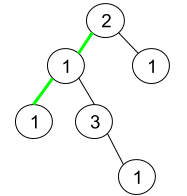
输入：root = [2,1,1,1,3,null,null,null,null,null,1]
输出：1
解释：上图为给定二叉树。总共有 3 条从根到叶子的路径：绿色路径 [2,1,1] ，路径 [2,1,3,1] 和路径 [2,1] 。
这些路径中只有绿色路径是伪回文路径，因为 [2,1,1] 存在回文排列 [1,2,1] 。
示例 3：

输入：root = [9]
输出：1
 

提示：

给定二叉树的节点数目在 1 到 10^5 之间。
节点值在 1 到 9 之间。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/pseudo-palindromic-paths-in-a-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

前序遍历二叉树，用一个数字来记录每个数出现的次数，若是出现偶数个或者之后一个是奇数个，则为true，次数 + 1。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int[] arr = new int[10];
    int count = 0;

    public int pseudoPalindromicPaths(TreeNode root) {
        find(root);
        return count;
    }

    private void find(TreeNode node) {
        arr[node.val] += 1;
        if (node.left == null && node.right == null) {
            boolean flag = false;
            for (int i = 1; i <= 9; i++) {
                if ((arr[i] & 1) != 0) {
                    if (flag) {
                        arr[node.val] -= 1;
                        return;
                    }
                    flag = true;
                }
            }
            count++;
            arr[node.val] -= 1;
            return;
        }
        if (node.left != null) {
            find(node.left);
        }
        if (node.right != null) {
            find(node.right);
        }
        arr[node.val] -= 1;
    }
}