leetcode 938. 二叉搜索树的范围和

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

 

示例 1：

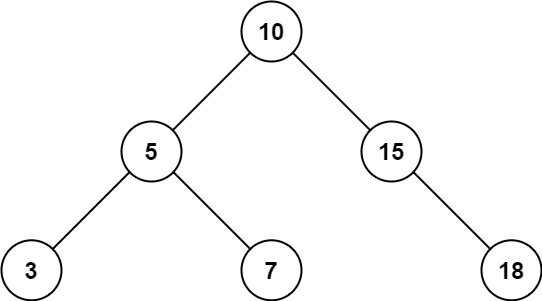
输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32
示例 2：

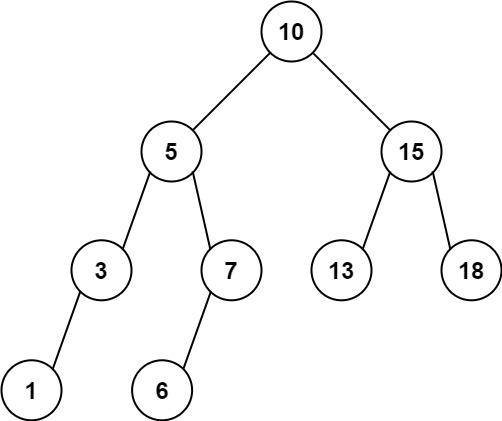
输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23
 

提示：

树中节点数目在范围 [1, 2 * 104] 内
1 <= Node.val <= 105
1 <= low <= high <= 105
所有 Node.val 互不相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/range-sum-of-bst
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

采用前序遍历，判断节点的值，若是在范围内，则累加。最后返回累加的值。

方法一，迭代

    public int rangeSumBST(TreeNode root, int low, int high) {

        Stack<TreeNode> stack = new Stack<>();
        stack.add(root);
        int sum = 0;
        while (!stack.isEmpty()) {

            TreeNode node = stack.pop();
            int val = node.val;
            
            if (val >= low && val <= high) {
                sum += val;
                if (node.left != null) {
                    stack.add(node.left);
                }
                if (node.right != null) {
                    stack.add(node.right);
                }
            } else if (val < low) {
                if (node.right != null) {
                    stack.add(node.right);
                }
            } else {
                if (node.left != null) {
                    stack.add(node.left);
                }
            }
        }
        return sum;
    }

 

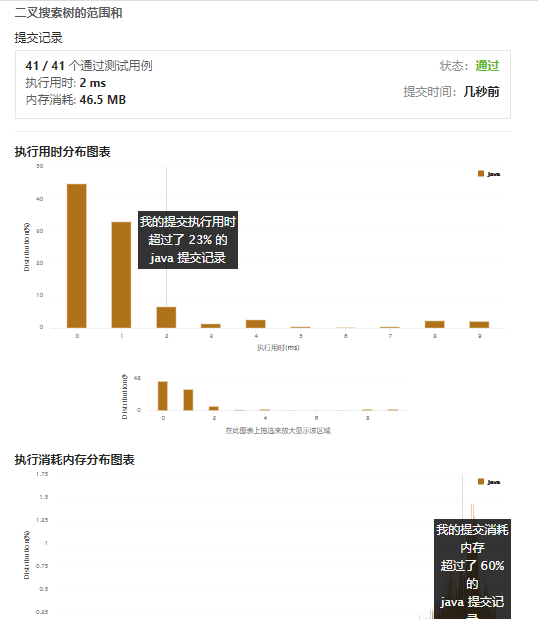
方法二，递归

   public int rangeSumBST(TreeNode root, int low, int high) {
        int sum = 0;
        if (root == null) {
            return 0;
        }
        int val = root.val;
        if (low <= val && val <= high) {
            sum += val;
            sum += rangeSumBST(root.left, low, high);
            sum += rangeSumBST(root.right, low, high);
        }  else if (val < low) {
            if (root.right != null) {
                sum += rangeSumBST(root.right, low, high);
            }
        } else {
            if (root.left != null) {
                sum += rangeSumBST(root.left, low, high);
            }
        }
        return sum;
    }

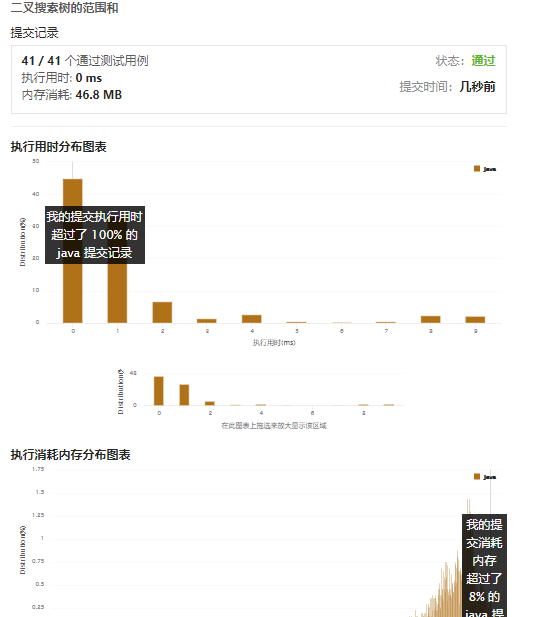
从上面看出，迭代的时间复杂度高，递归的时间复杂度低。