三、二叉树的遍历与创建（先序、中序、后序、层次）

 

　　二叉树的遍历是指按某条搜索路径访问二叉树中的每个节点一次且只有一次。

　　按照根、左子树和右子树的访问先后顺序不同，二叉树的遍历可以有6种方案：DLR、LDR、LRD、DRL、RDL、RLD。如果限定先左后右（先左子树后右子树），则只有前3种遍历方案：DLR、LDR、LRD。按照根的访问顺序不同，根在前面称为先序遍历（DLR），根在中间称为中序遍历（LDR），根在最后称为后序遍历（LRD）。

 

一、先序遍历

先序遍历是指先访问根，然后先序遍历左子树，再先序遍历右子树。
算法步骤：
如果二叉树为空，则空操作，否则：
　　1）访问根节点；
　　2）先序遍历左子树；
　　3）先序遍历右子树。
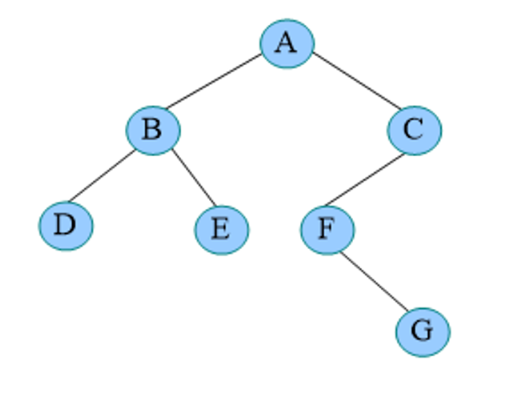
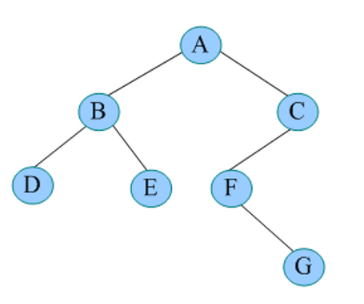
先序遍历秘籍：访问根，先序遍历左子树，左子树为空或已遍历才可以遍历右子树。

如: 下面图片的顺序是 A->B->D->E->C->F->G

void preorder(Btree T)
{
    if(T)
    {
        cout << T->data << endl;   // 根
        preorder(T->lChild);       // 左子树
        preorder(T->rchild);       // 右子树
    }
}

二、中序遍历

中序遍历是指中序遍历左子树，然后访问根，再中序遍历右子树。
算法步骤：
如果二叉树为空，则空操作，否则：
　　1）中序遍历左子树；
　　2）访问根节点；
　　3）中序遍历右子树。
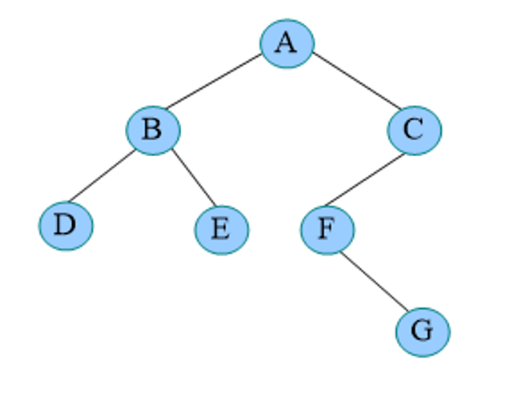
中序遍历秘籍：中序遍历左子树，左子树为空或已遍历才可以访问根，中序遍历右子树。

如: 下面图片的顺序是 D->B->E->A->F->G->C

 

 

void inorder(Btree T)
{
    if(T)
    {
        inorder(T->lchild);      // 左子树
        cout << T->data << endl; // 根
        inorder(T->rchild);      // 右子树
    }
}

三、后序遍历

后序遍历是指后序遍历左子树，后序遍历右子树，然后访问根。
算法步骤：
如果二叉树为空，则空操作，否则：
　　1）后序遍历左子树；
　　2）后序遍历右子树；
　　3）访问根节点。
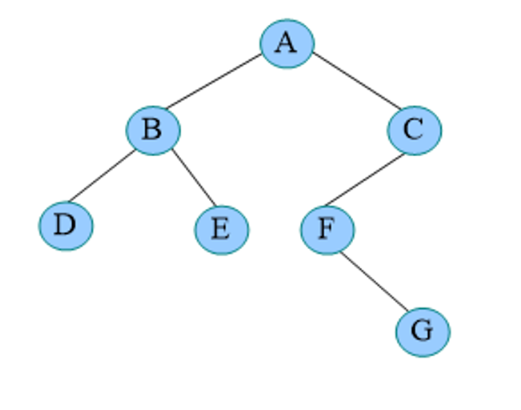
后序遍历秘籍：后序遍历左子树，后序遍历右子树，左子树、右子树为空或已遍历才可以访问根。

如: 下面图片的顺序是 D->E->B->G->F->C->A

 

 

void posorder(Btree T)
{
    if(T)
    {
        posorder(T->lchild);     // 左子树
        posorder(T->rchild);     // 右子树
        cout << T->data << endl; // 根
    }
}

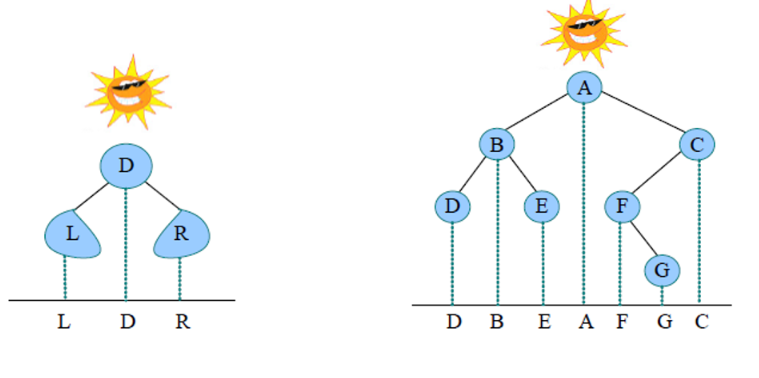
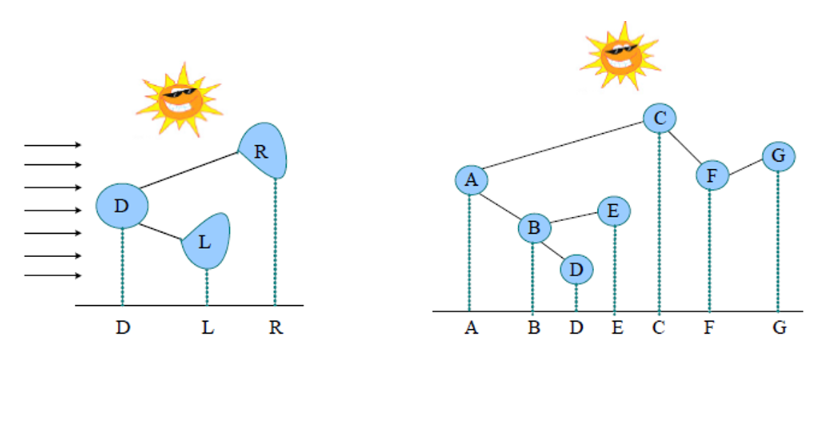
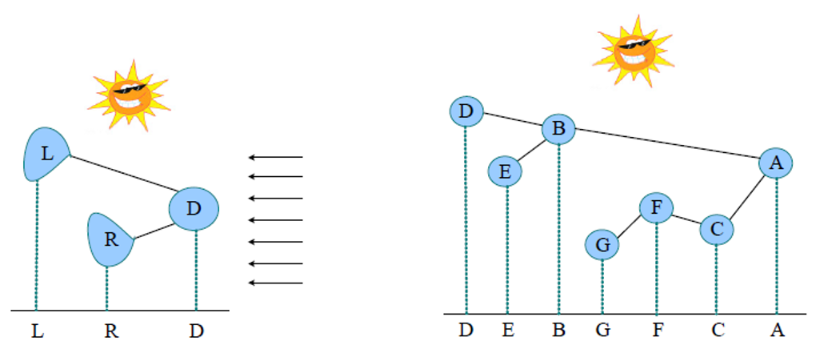
四、投影法求遍历序列

4.1 投影法求中序遍历

中序遍历就像在无风的情况下，遍历顺序为左子树、根、右子树，太阳直射，将所有的节点投影到地上。

4.3 投影法求先序遍历

先序遍历就像在左边大风的情况下，将二叉树的树枝刮向右方，且顺序为根、左子树、右子树，太阳直射，将所有的节点投影到地上。

4.3 投影法求后序遍历

后序遍历就像在右边大风的情况下，将二叉树的树枝刮向左方，且顺序为左子树、右子树、根，太阳直射，将所有的节点投影到地上。

 

 

五、层次遍历

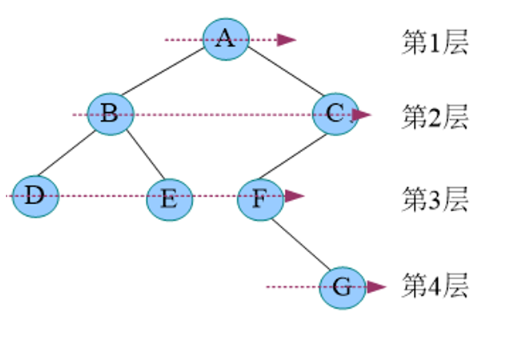
层次遍历，即按照层次的顺序从左向右进行遍历。
层次遍历秘籍：首先遍历第1层，然后第2层……同一层按照从左向右的顺序访问，直到最后一层。

/*
    通过观察可以发现，先被访问的节点，其孩子也先被访问，先来先服务，因此可以用队列实现。使用队列对下面二叉树进行层次遍历。
*/
bool Leveltralverse(Btree T)
{
    Btree p;
    if(!T)
    {
        return false;
    }
    queue<Btree>Q;  // 创建一个指针队列， 指针类型
    Q.push(T);      // 根指针入队
    while(!Q.empty())
    {
        p = Q.front();  // 取出队头元素
        Q.pop();        // 队头元素出队
        cout << p->data << "  ";
        if(p->rchild)
        {
            Q.push(p->lchild);  // 左孩子指针入队
        }
        if(p->rchild)
        {
            Q.push(p->rchild);  // 有孩子指针入队
        }
    }
    return true;
}

 

六、二叉树的创建

二叉树存储可以是顺序存储,也可以是链式存储。
顺序存储的浪费空间较大，所以一般采用链式存储。

https://www.cnblogs.com/wangyong123/articles/16123087.html#_lab2_1_0

补空法指如果左子树或右子树为空，则用特殊字符补空，例如“#”。然后根据先序遍历序列递归创建二叉树。

二叉树补空后的先序遍历结果为ABD##E##CF#G###。

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;

typedef struct Bnode
{
    char data;
    struct Bnode *lchild, *rchild;
}Bnode, *Btree;

// 递归创建二叉树
void createTree(Btree &T)
{
    char ch;
    cin >> ch;
    if (ch == '#')
    {
        T = NULL; // 递归结束，建空树
    }
    else
    {
        T = new Bnode;
        T->data = ch;
        createTree(T->lchild);  // 递归创建左子树
        createTree(T->rchild);  // 递归创建右子树
    }
}

int main()
{
    Btree BTree;
    cout << "按先序次序输入二叉树中结点的值（孩子为空时输入#），创建一棵二叉树" << endl;
    createTree(BTree);//创建二叉树
    return EXIT_SUCCESS;
}


/*测试数据
ABD##E##CF#G###
*/

 

七、二叉树创建与遍历代码整合

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<string>
#include<queue>//引入队列头文件
using namespace std;

typedef struct Bnode
{
    char data;
    struct Bnode *lchild, *rchild;
}Bnode, *BTree;

// 创建二叉树
void createTree(BTree &T)
{
    char ch;
    cin >> ch;
    if (ch == '#')
    {
        T = NULL;               // 递归结束，建空树
    }
    else
    {
        T = new Bnode;
        T->data = ch;
        createTree(T->lchild);  // 递归创建左子树
        createTree(T->rchild);  // 递归创建右子树
    }
}

// 先序遍历
void preorder(BTree &T)
{
    if (T)
    {
        cout << T->data << "  ";
        preorder(T->lchild);
        preorder(T->rchild);
    }
}

// 中序遍历
void inorder(BTree &T)
{
    if (T)
    {
        inorder(T->lchild);
        cout << T->data << "  ";
        inorder(T->rchild);
    }
}

// 后续遍历
void posorder(BTree &T)
{
    if (T)
    {
        posorder(T->lchild);
        posorder(T->rchild);
        cout << T->data << "  ";
    }
}

// 层次遍历
bool leveltraverse(BTree &T)
{
    BTree p;
    if (!T)
    {
        return false;
    }
    queue<BTree>Q;  //创建一个队列，指针类型
    Q.push(T);      // 根指针入队
    while (!Q.empty())
    {
        p = Q.front(); // 取出队头元素
        Q.pop();
        cout << p->data << "  ";
        if (p->lchild)
        {
            Q.push(p->lchild);
        }
        if (p->rchild)
        {
            Q.push(p->rchild);
        }
    }
    return true;
}

int main()
{
    BTree btree;
    cout << "按先序次序输入二叉树中结点的值（孩子为空时输入#），创建一棵二叉树" << endl;
    createTree(btree);//创建二叉树
    cout << endl;
    cout << "二叉树的先序遍历结果：" << endl;
    preorder(btree);//先序遍历二叉树       A  B  D  E  C  F  G
    cout << endl;
    cout << "二叉树的中序遍历结果：" << endl;
    inorder(btree);//中序遍历二叉树        D  B  E  A  F  G  C
    cout << endl;
    cout << "二叉树的后序遍历结果：" << endl;
    posorder(btree);//后序遍历二叉树       D  E  B  G  F  C  A
    cout << endl;
    cout << "二叉树的层次遍历结果：" << endl;
    leveltraverse(btree);//层次遍历二叉树  A  B  C  D  E  F  G
}

/*测试数据
ABD##E##CF#G###
*/