二、二叉树的性质

一、二叉树的性质

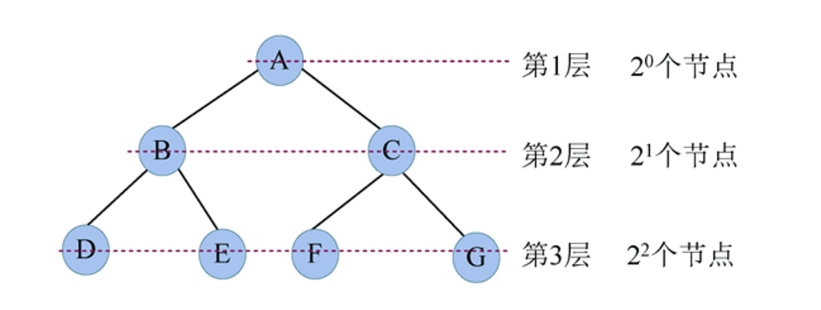
1.1 二叉树 i 层最多节点数（2^i-1）

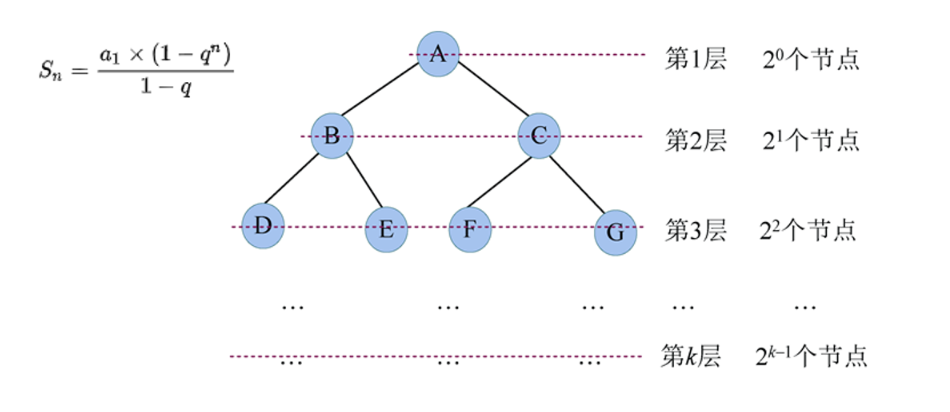
性质1：在二叉树的第i层上至多有2^i-1个节点。

 

1.2 二叉树深度 k 最多总节点数（2^k-1）

性质2：深度为k的二叉树至多有2^k−1个节点。

1.3 叶子数与度的关系

性质3：对于任何一棵二叉树，若叶子数为n₀，度为2的节点数为n₂，则n₀=n₂+1。

叶子： 度数是0的节点称为叶子

n_0：度数是 0 的节点

n_1：度数是 1 的节点

n₂：度数是 2 的节点

b ： 分支数

 

节点总数 =  n₀ + n₁ + n₂（从上往下看,度数为0,1,2的节点数之和）

节点总数 = 分支数 + 1  =   n₁ + 2n₂ + 1 （ 从下往上看，每一个节点有一个分支，然后加上根节点）            

分支数 = n₁ + 2n₂  （度数是1的产生一个分支，度数是2的产生两个分支）

推导：  n₀ + n₁ + n_{2 =} n₁ + 2n₂ + 1  ==>  n₀=n₂+1

 

 

满二叉树：一棵深度为k且有2^k−1个节点的二叉树。满二叉树每一层都“充满”了节点，达到最大节点数。
完全二叉树：除了最后一层外，每一层都是满的（达到最大节点数），最后一层节点是从左向右出现的。
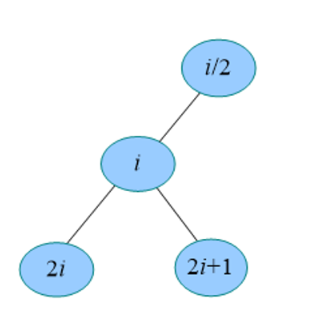
深度为k的完全二叉树，当且仅当其每一个节点都与深度为k 的满二叉树中编号1～n的节点一一对应。

1.4 n个节点完全二叉树的深度

性质4：具有n个节点的完全二叉树的深度必为 [log₂ⁿ] + 1。

 

 

 

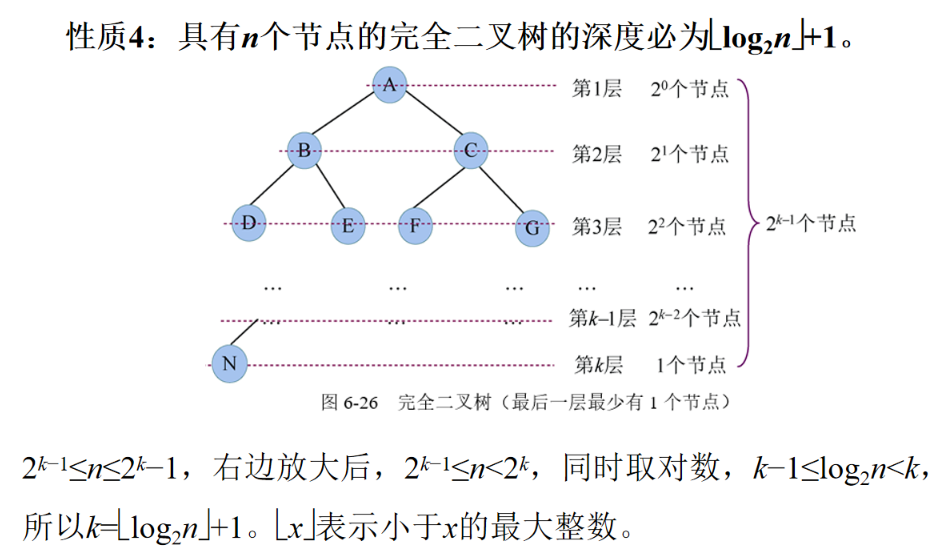
 2^k−1 ≤ n ≤ 2^k-1，右边放大后，2^k−1  ≤ n < 2^k，同时取对数，k−1 ≤ log₂ⁿ < k，所以 k = [log₂ⁿ] + 1 。[x] 表示小于x的最大整数。

1.5 二叉树的编号规则

性质5：对于完全二叉树，若从上至下、从左至右编号，则编号为i的节点，其左孩子编号必为2i，其右孩子编号必为2i +1，其双亲的编号必为i/2。

 

 

 

 

1.6 例题测试

例题1：一棵完全二叉树有1 001个节点，其中叶子节点的个数是多少？
　　最后一个节点是1001， 其父亲是500，那么其父亲以后的节点都没有孩子了，叶子数 = 1001-500 = 501


例题2：一棵完全二叉树第6层有8个叶子，则该完全二叉树最少有多少节点，最多有多少个节点？
　　方法一:
　　　　第六层有个叶子，说明该完全二叉树最少六层，最多七层。
　　　　当总共六层: 说明前五层是满的 + 第六层 = 2^5 - 1 + 8 = 39
　　　　当总共七层: 完全二叉树第六层应该有 = 2^5 = 32; 前面六层总共 = 2^6 - 1 = 63;
　　　　第六层 8 个叶子，说明第七层 = ( 32 - 8 ) * 2 = 48
　　　　总共 = 63 + 48 = 111
　　方法二:
　　　　如果第七层是满的，那么第六层的8个叶子需要增加16个节点，总共 = 2^7 - 1 - 16 = 111

 

二、二叉树的存储

2.1 二叉树的顺序存储

二叉树也可以采用顺序存储，完全二叉树的节点层次编号，依次存放二叉树中的数据元素。

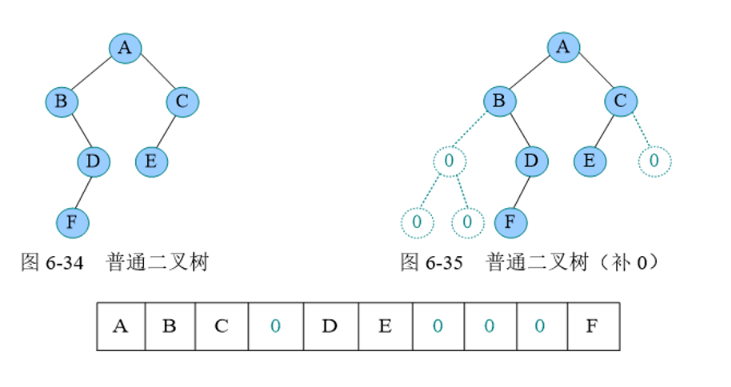
2.2 二叉树的链式存储

/*
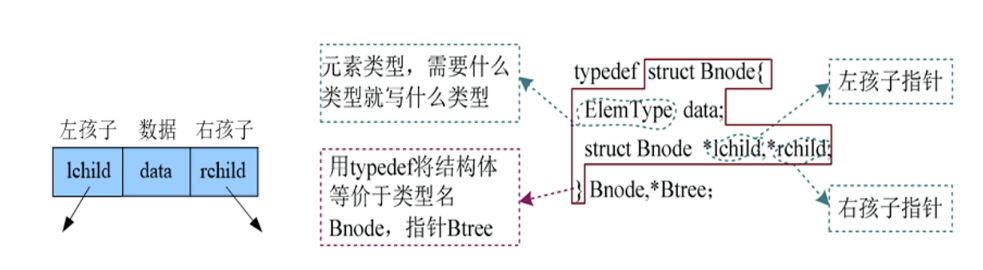
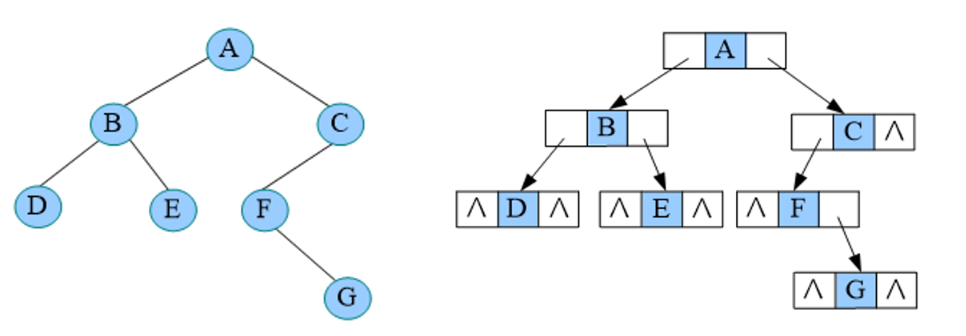
    二叉树的链式存储：每个节点包含一个数据域，存储节点信息；还包含两个指针域，指向左右两个孩子。这种存储方式称为二叉链表
*/
typedef struct Bnode
{
    ElemType data;
    struct Bnode *lchild, *rchild;
}Bnode, *Btree;

 

 

 

 

 

三、二叉搜索树和平衡二叉树

　　二叉搜索树，是指二叉树中的节点按照一定的规则进行排序，使得对二叉树中元素访问更加高效。二叉搜索树的放置规则是：任何节点的元素值一定大于其左子树中的每一个节点的元素值，并且小于其右子树的值。因此从根节点一直向左走，一直到无路可走，即得到最小值，一直向右走，直至无路可走，可得到最大值。那么在二叉搜索树中找到最大元素和最小元素是非常简单的事情。下图为二叉搜索树：

 

 

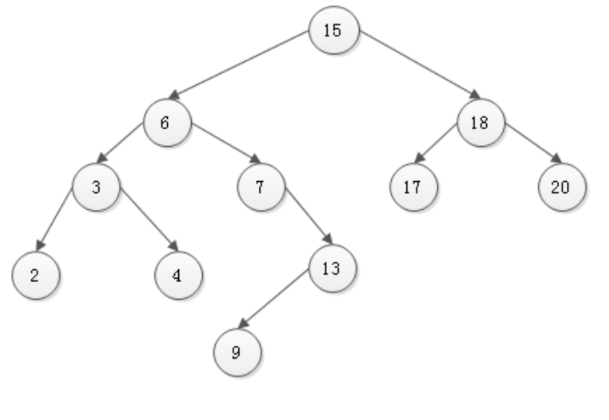
　　上面我们介绍了二叉搜索树，那么当一个二叉搜索树的左子树和右子树不平衡的时候，那么搜索依据上图表示，搜索9所花费的时间要比搜索17所花费的时间要多，由于我们的输入或者经过我们插入或者删除操作，二叉树失去平衡，造成搜索效率降低。
　　所以我们有了一个平衡二叉树的概念，所谓的平衡不是指的完全平衡。
　　平衡二叉树： 左子树的深度与与右子树的深度的高度差绝对值不能大于1，这棵树的字数也必须是平衡二叉树