一、树、二叉树与森林的转换

一、树与二叉树

1.1 树

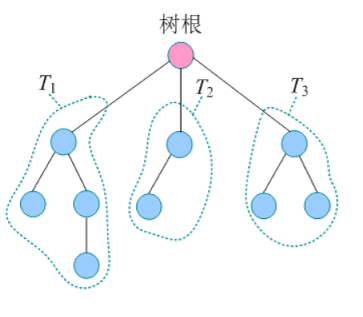
树是n（n≥0）个节点的有限集合，当n=0时，为空树。任意一棵非空树，满足：
①有且仅有一个被称为根的节点；
②除根节点外，其余节点可分为m个互不相交的有限集T1, T2, …, Tm，每一个集合本身又是一棵树，称为根的子树。

1.2 二叉树

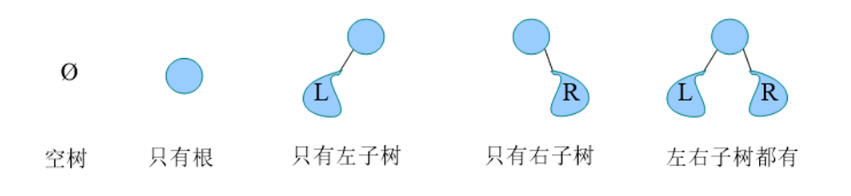
二叉树（binary tree）是n（n≥0）个节点构成的集合，当n=0时，为空树。任意一棵非空二叉树，满足：
1）有且仅有一个称为根的节点；
2）除根节点以外，其余节点分为两个互不相交的子集T1和T2，分别称为T的左子树和右子树，且T1和T2本身都是二叉树。

二、树的存储

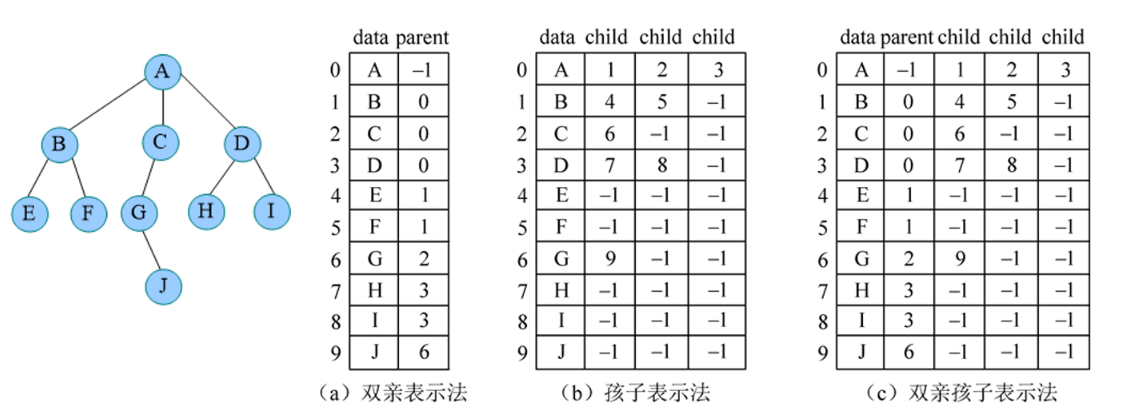
树形结构是一对多的关系，除了树根，每个节点都有一个唯一的直接前驱（双亲）；除了叶子，每个节点都有一个或多个直接后继（孩子）。那么如何将数据及它们之间的逻辑关系存储起来呢？
可以采用顺序存储和链式存储。

2.1 顺序存储

树的顺序存储分为双亲表示法、孩子表示法和双亲孩子表示法。

2.2 链式存储

树的链式存储分为孩子链表表示法和孩子兄弟表示法。

 

 

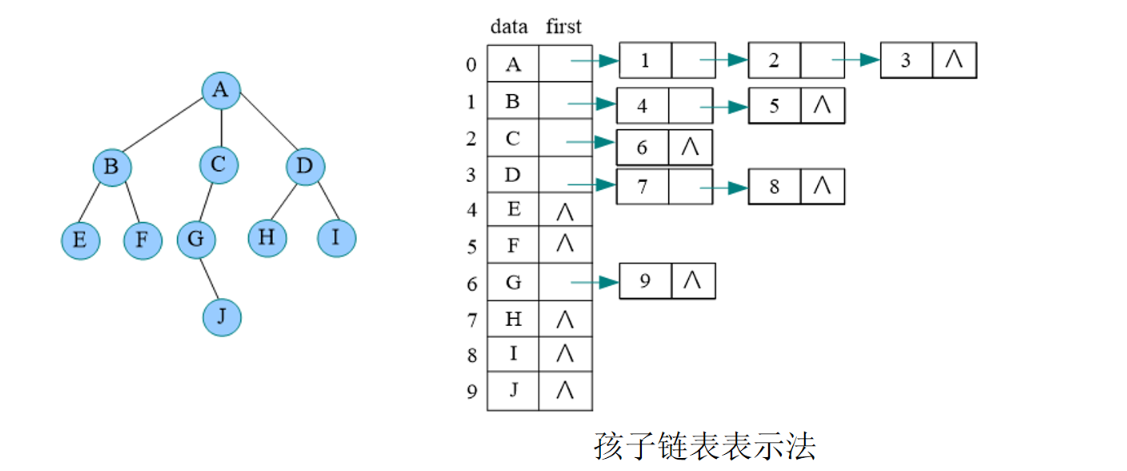
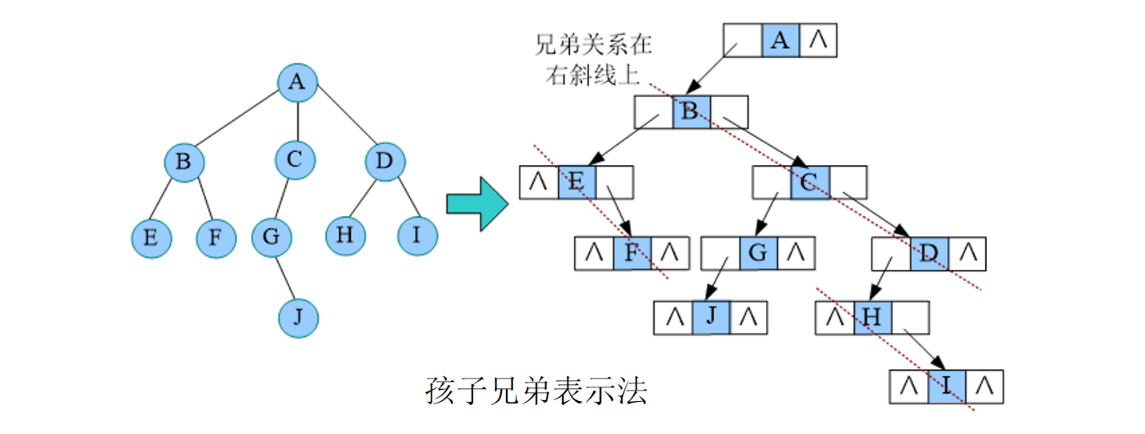
孩子兄弟表示法的秘诀：长子当作左孩子，兄弟关系向右斜。

 

三、树、二叉树、森林之间转换

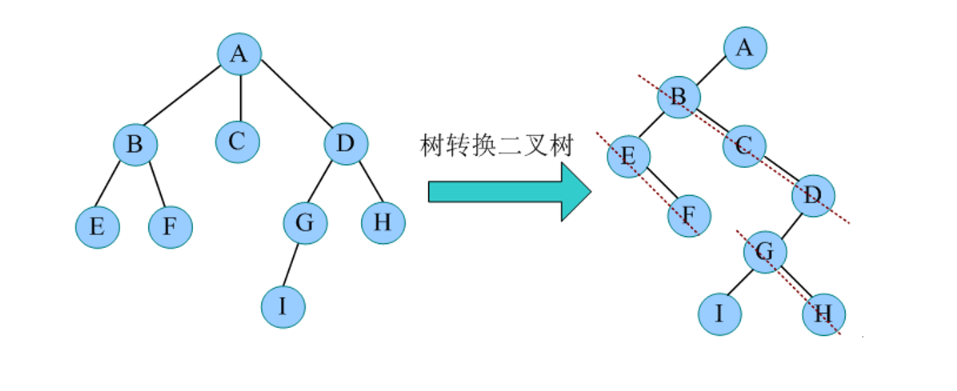
3.1 树转换为二叉树

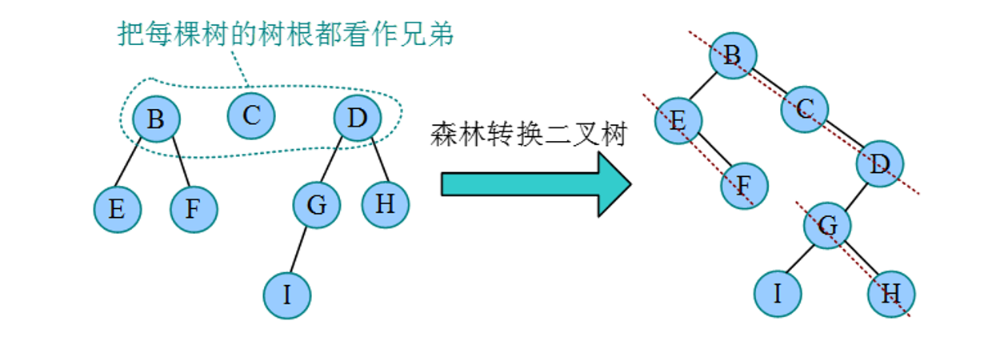
树转换为二叉树的秘诀：长子当作左孩子，兄弟关系向右斜。

 

3.2 森林转换为二叉树

把森林中的每棵树的树根看作兄弟关系，把森林中的每一棵树转换成二叉树，然后把每棵树的根节点连接在右斜线上。

3.3. 二叉树还原森林

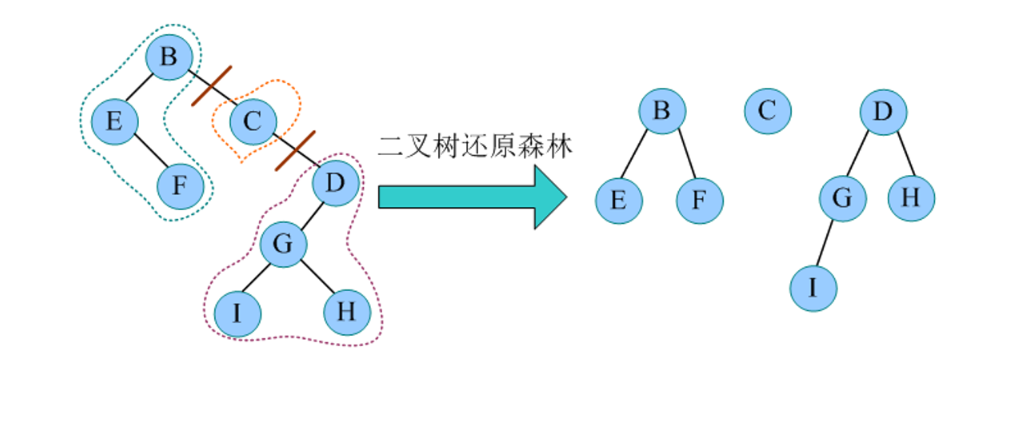
 二叉树还原森林为的秘诀：右斜线上每个节点为一棵树的根，将每棵二叉树转换为树。