深度卷积网络原理—非线性激活的必要性

假设有如上图所示的神经网络实例图

网络描述如下：

1）有2个输入，即图中的x₁、x₂

2）有3个神经元，即途中的b₁、b₂、b₃

3）共2层网络。第1层的神经元是b₁、b₂，第2层的神经元是b₃.可将中间层称为隐层。例如途中的b₁、b₂就属于隐层

4）有6个权重(w₁₁到w₂₃）。最终输出为OUT。

 

神经元b₁的输出是： x₁w₁₁+x₂w₂₁+b₁

神经元b2的输出是：x₁w₁₂+x₂w₂₂+b₂

 

如果没有非线性激活，那么最终的输出OUT的计算公式是：

OUT=（x₁w₁₁ + x₂w₂₁ + b₁)* w₁₃ + (x₁w₁₂ + x₂w₂₂ + b₂)*w₂₃ + b₃

        =x₁*(w₁₁w₁₃ + w₁₂w₂₃) + x₂ * (w₂₁w₁₃ + w₂₂w₂₃)+(b₁w₁₃ +b₂w₂₃ +b₃)

 

从上面的公式可以看出，虽然用了3个神经元，但这个网络对于x₁和x₂仍然是线性的，完全等价于1个神经元的效果。

如下图：

 

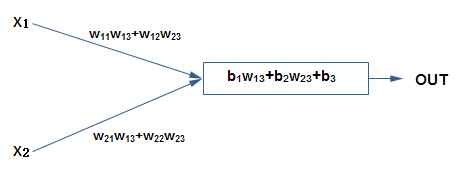
因此，如果只是把神经元简单的连接在一起，不加入非线性处理，最终得到的仍然是线性函数，无法完成描述各种复杂的现象，可看出在神经元的输出时需要一个非线性函数是必要的。

 

若非线性激活函数对于中间层神经元是f，对于最终输出神经元是g，那么，对于此前的网络，最终的输出会变为：

OUT=g(f(x₁w₁₁ + x₂w₂₁ +  b₁)* w₁₃ + f(x₁w₁₂ + x₂w₂₂+b₂)*w₂₃ + b₃)

由于f和g都是非线性的，于是最终可得到非线性的网络输出，即可拟合出复杂的数据。