国密随机数检测--1/15 单比特频数检测

最近研究随机数检测，主要学习了一下NIST和国密检测，这里整理了国密15项检测规项目的原理，数学表达式以及python源码。

15项检测项目分别为单比特频数检测、块内频数检测、扑克检测、重叠子序列检测、游程总数检测、游程分布检测、块内最大“1”游程检测、二元推导检测、自相关检测、矩阵秩检测、累加和检测、近似熵检测、线性复杂度检测、 Maurer通用统计检测、离散傅立叶检测。

规定了商用密码应用中的随机性检测指标和检测方法，适用于对随机数发生器产生的二元序列的随机性检测。

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

1/15 单比特频数检测  monobit frequency test

a) 将待检序列ε 中的 0 和 1 分别转换成-1 和 1， X _i = 2ε_i -1  (1 ≤ i n ≤ )。

b) 对其累加求和得

c) 计算统计值

 

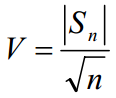
d) 计算

erfc为余误差函数。

 

e) 如果

 

 则认为待检测序列通过但比特数检测。

 

原理：

单比特频数检测是最基本的检测，用来检测一个二元序列中0和1的个数是否相近。也就是说，若已知一个长度为n的二元序列，检测改序列是否有较好的0、1平衡性。令n₀、n₁分别表示该序列中0和1的数目。对一个随机序列，当其长度充分大时，其统计值V应该服从正态分布

 

 

参数要求：

n>100 

 

不通过分析：

0或1个数太小

 

测试demo

import math

def count_ones_zeroes(bits):
    ones = 0
    zeroes = 0
    for bit in bits:
        if (bit == 1):
            ones += 1
        else:
            zeroes += 1
    return (zeroes,ones)

def monobit_test(bits):
    n = len(bits)
    
    zeroes,ones = count_ones_zeroes(bits)
    s = abs(ones-zeroes)
    print ("  Ones count   = %d" % ones)
    print ("  Zeroes count = %d" % zeroes)
    
    p = math.erfc(float(s)/(math.sqrt(float(n)) * math.sqrt(2.0)))
    
    success = (p >= 0.1)
    return (success,p,None)

bits=[1,1,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,0,0,1,0,1,1,1,1,1,
          0,1,1,1,1,1,0,0,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0,0,0,0,
          0,0,0,0,0,1,0,0,0,1,0,0,0,0,1,1,0,0,1,0,0,0,0,1,0,1,0,
          0,1,1,0,0,0,1,1,1,0,1,0,0,0,0,1,0,0,1,0,1,0,1,0,0,1,1,
          0,0,0,1,1,0,1,0,1,1,1,0,0,1,1,1,1,1,0,0,0] 


if __name__ == "__main__":
    s1,s2,s3= monobit_test(bits)
    print(s1)
    print("p value is %s" %s2)