压缩感知(十)
压缩感知仿真验证
一维信号重建实验
clear; close all; choice_transform=1; choice_Phi=0; n = 512; t = [0: n-1]; f = cos(2*pi/256*t) + sin(2*pi/128*t); % n = length(f); a = 0.2; m = double(int32(a*n)); switch choice_transform case 1 ft = dct(f); disp('ft = dct(f)') case 0 ft = fft(f); disp('ft = fft(f)') end disp(['ÐźÅÏ¡Êè¶È£º',num2str(length(find((abs(ft))>0.1)))]) figure('name', 'A Tone Time and Frequency Plot'); subplot(2, 1, 1); plot(f); xlabel('Time (s)'); % ylabel('f(t)'); subplot(2, 1, 2); switch choice_transform case 1 plot(ft) disp('plot(ft)') case 0 plot(abs(ft)); disp('plot(abs(ft))') end xlabel('Frequency (Hz)'); % ylabel('DCT(f(t))'); switch choice_Phi case 1 Phi = PartHadamardMtx(m,n); case 0 Phi = sqrt(1/m) * randn(m,n); end f2 = (Phi * f')'; % f2 = f(1:2:n); switch choice_transform case 1 Psi = dct(eye(n,n)); disp('Psi = dct(eye(n,n));') case 0 Psi = inv(fft(eye(n,n))); disp('Psi = inv(fft(eye(n,n)));') end A = Phi * Psi; % A = Phi * Psi cvx_begin; variable x(n) complex; % variable x(n) ; minimize(norm(x,1)); subject to A*x == f2'; cvx_end; figure; subplot(2,1,2); switch choice_transform case 1 plot(real(x)); disp('plot(real(x))') case 0 plot(abs(x)); disp('plot(abs(x))') end title('Using L1 Norm£¨Frequency Domain£©'); % ylabel('DCT(f(t))'); xlabel('Frequency (Hz)'); switch choice_transform case 1 sig = dct(real(x)); disp('sig = dct(real(x))') case 0 sig = real(ifft(full(x))); disp('sig = real(ifft(full(x)))') end subplot(2,1,1); plot(f) hold on;plot(sig);hold off title('Using L1 Norm (Time Domain)'); % ylabel('f(t)'); xlabel('Time (s)'); legend('Original','Recovery') for K = 1:100 theta = CS_OMP(f2,A,K); % figure;plot(dct(theta));title(['K=',num2str(K)]) switch choice_transform case 1 re(K) = norm(f'-(dct(theta))); case 0 re(K) = norm(f'-real(ifft(full(theta)))); end end theta = CS_OMP(f2,A,find(re==min(min(re)))); disp(['×î¼ÑÏ¡Êè¶ÈK=',num2str(find(re==min(min(re))))]); % theta = CS_OMP(f2,A,10); figure;subplot(2,1,2); switch choice_transform case 1 plot(theta); disp('plot(theta)') case 0 plot(abs(theta)); disp('plot(abs(theta))') end title(['Using OMP(Frequence Domain) K=',num2str(find(re==min(min(re))))]) switch choice_transform case 1 sig2 = dct(theta); disp('sig2 = dct(theta)') case 0 sig2 = real(ifft(full(theta))); disp('sig2 = real(ifft(full(theta)))') end subplot(2,1,1);plot(f);hold on; plot(sig2) hold off; title(['Using OMP(Time Domain) K=',num2str(find(re==min(min(re))))]); legend('Original','Recovery')
一维信号仿真结果
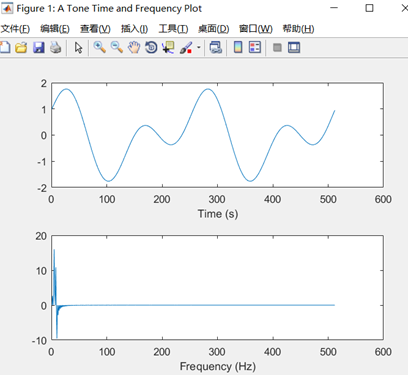
如上图所示,为原始信号f = cos(2*pi/256*t) + sin(2*pi/128*t),及其频域图(频域稀疏)。
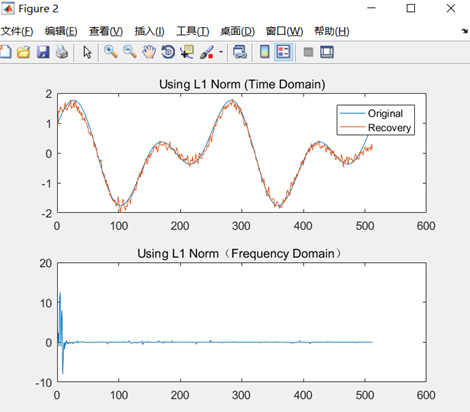
取原信号的20%,使用L1范数算法对原信号进行恢复重建,效果如上图所示,蓝色为原始信号,红色为恢复信号。
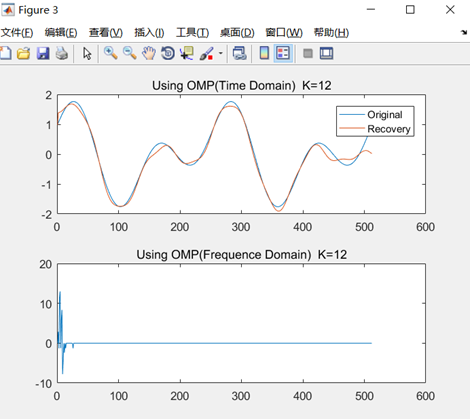
取原信号的20%,使用OMP算法对原信号进行恢复重建,效果如上图所示,蓝色为原始信号,红色为恢复信号。
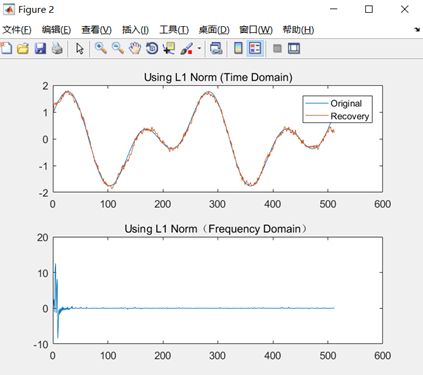
取原信号的30%,使用L1范数算法对原信号进行恢复重建,效果如上图所示,蓝色为原始信号,红色为恢复信号。

取原信号的30%,使用OMP算法对原信号进行恢复重建,效果如上图所示,蓝色为原始信号,红色为恢复信号。
小结:压缩感知原本就是为了信号(非图像)采集而生,所以在信号采集上有很强的实用性,甚至只需要原信号10~20%的信息,就可以复原出原信号的大部分特性。



