快速傅里叶变换(FFT)详解
快速傅里叶变换(FFT)详解
(这是我第一次写博,不喜勿喷...)
关于FFT已经听闻已久了,这次终于有机会在Function2的介绍下来了解一下FFT了。
快速傅里叶变换(Fast Fourier Transformation)简称FFT。在各大OI竞赛中也常有用到,也是一个十分优秀的可以装逼的好算法
在这篇blog中,有大量数学推导,因为我懒得写公式(好复杂,逃),所以用图片代替了╮(╯▽╰)╭,如有不适,望见谅(逃~~)。
基础知识:

多项式的度数:

多项式的线性空间

系数表达

向量的卷积

分治乘法(如果你急着和MM约会或机房要关门了,那跳过也无妨)


点值表达

插值

点值计算分析

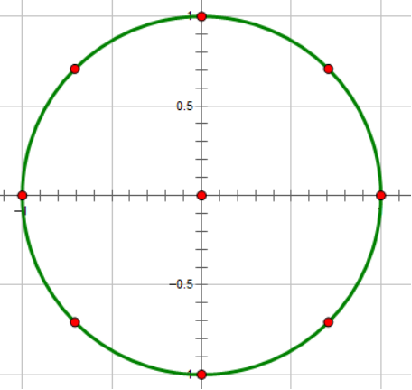
单位复数根

单位复数根的性质
- 消去引理
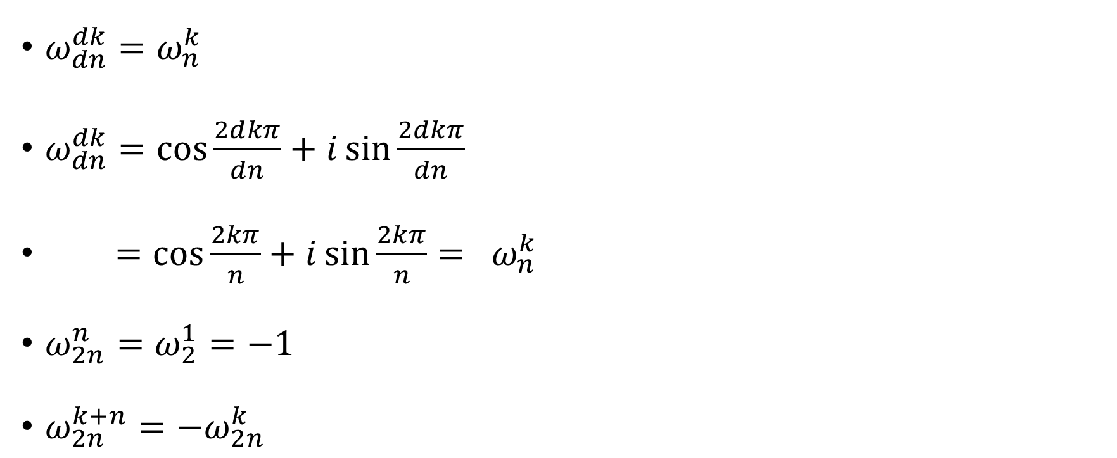
2.折半引理

3.求和引理
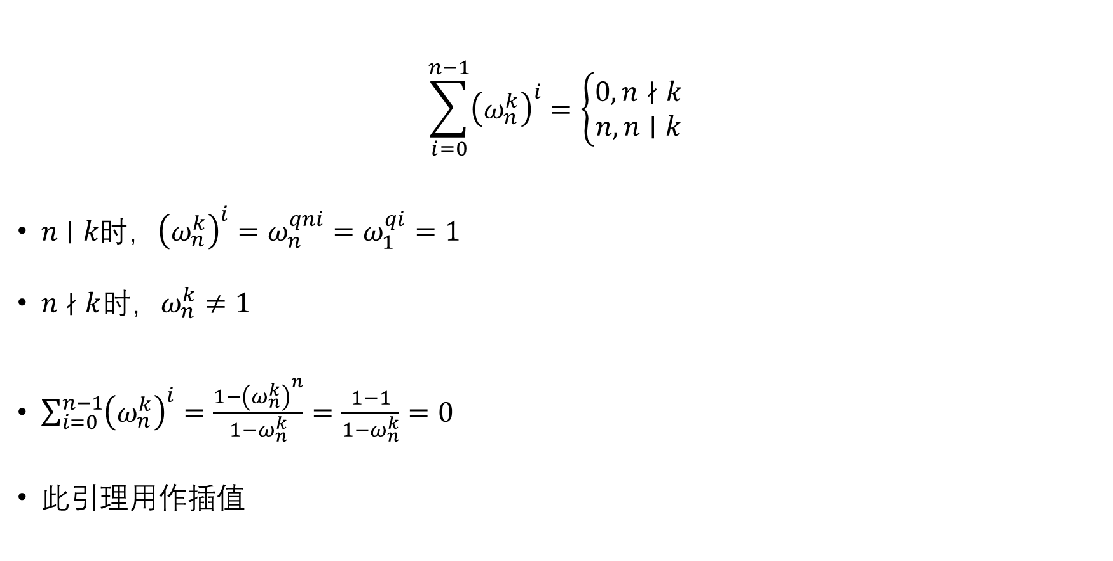
铺垫都铺完了,让我们一起进入DFT,FFT,IDFT的美妙世界吧!
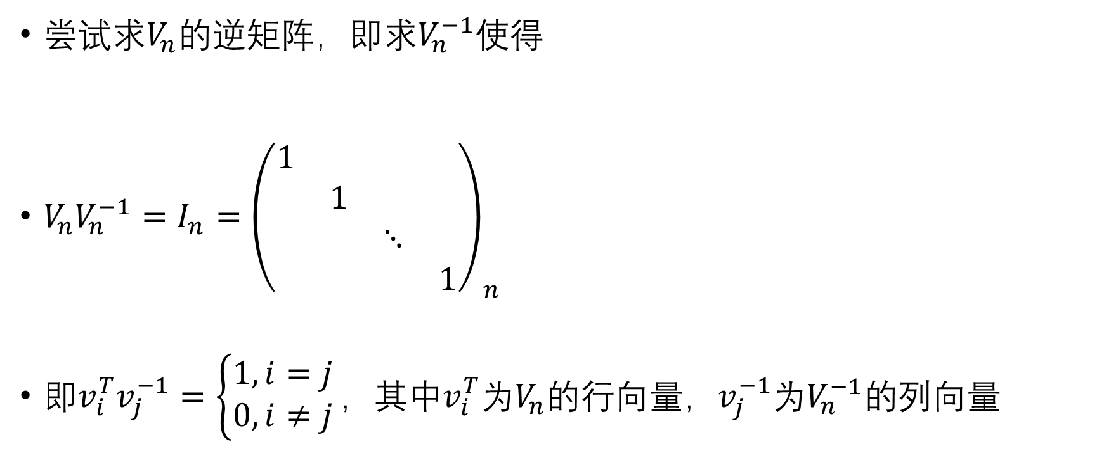
离散傅里叶变换(Discrete Fourier Transform 简称DFT)

快速傅里叶变换(FFT)(终于等到你~~)

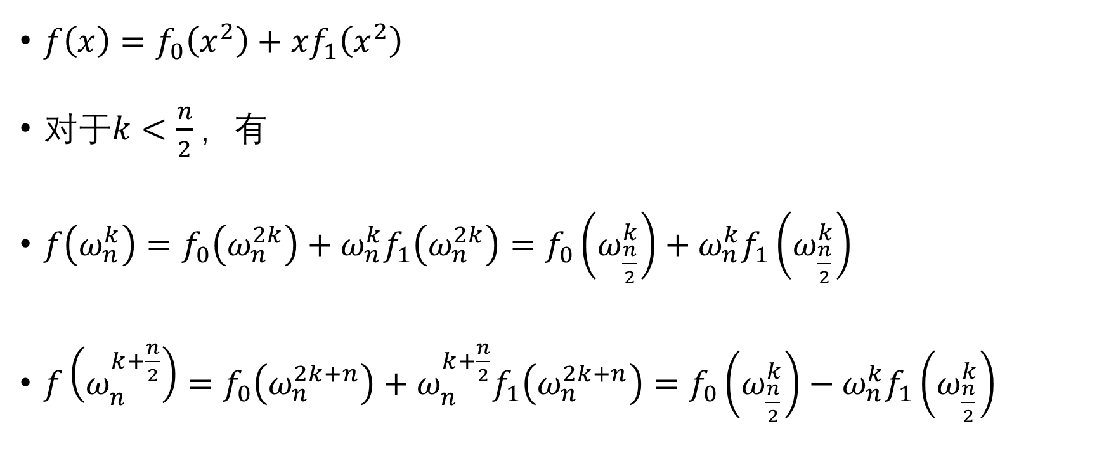

逆离散傅里叶变换(Inverse Discrete Fourier Transform 简称IDFT)

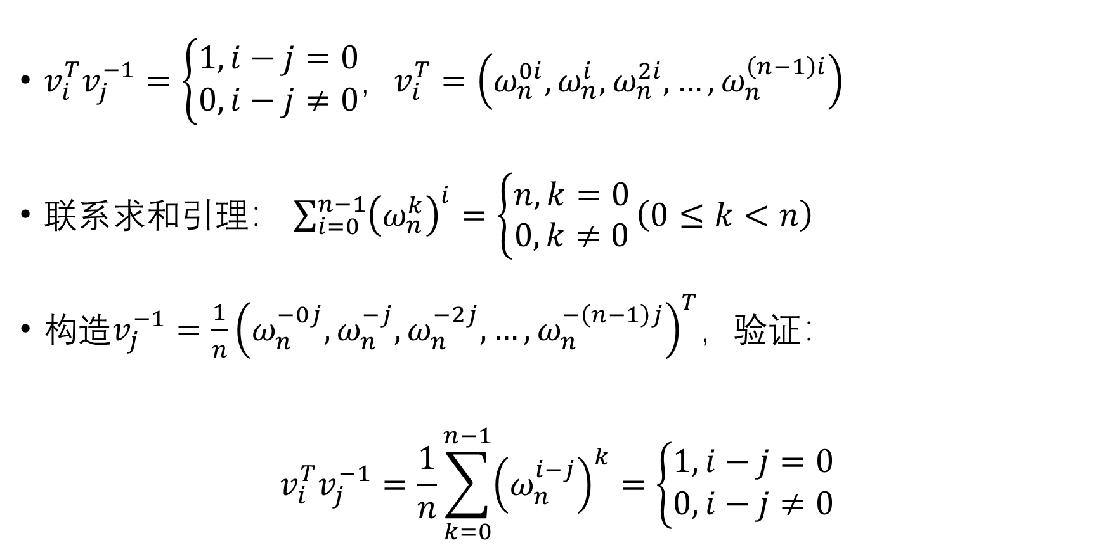

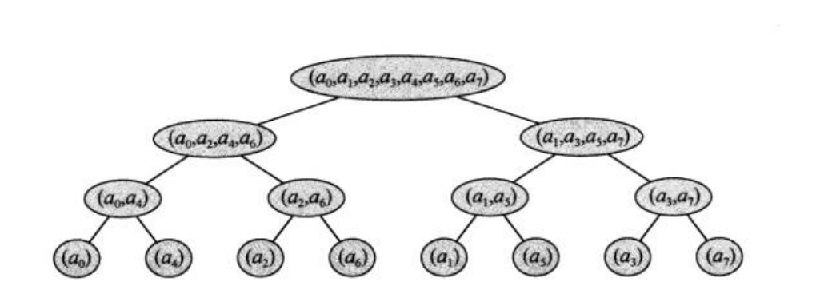
FFT的迭代实现
我们类似于需要像这样实现FFT:

知识点终于讲完了,接下来我们就要开始写板子了
板子题:uoj #34
代码附上~~
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 #include<cstdlib> 7 using namespace std; 8 const int mod=1e9+7; 9 const double pi=acos(-1); 10 struct cn 11 { 12 double x,y; 13 cn (double x=0,double y=0):x(x),y(y) {} 14 }a[300005],b[300005],c[300005]; 15 cn operator + (const cn &a,const cn &b) {return cn(a.x+b.x,a.y+b.y);} 16 cn operator - (const cn &a,const cn &b) {return cn(a.x-b.x,a.y-b.y);} 17 cn operator * (const cn &a,const cn &b) {return cn(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);} 18 void fft(cn a[],int n,int l,int f) 19 { 20 int rev[n+5]; 21 rev[0]=0; 22 for (int i=1; i<n; i++){ 23 rev[i]=(rev[i>>1]>>1)|((i&1)<<l-1); 24 if (i<rev[i]) swap(a[i],a[rev[i]]); 25 } 26 for (int i=1; i<n; i<<=1){ 27 cn wi(cos(pi/i),f*sin(pi/i)); 28 for (int j=0; j<n; j+=i*2){ 29 cn w(1,0); 30 for (int k=0; k<i; k++){ 31 cn x=a[j+k],y=w*a[j+k+i]; 32 a[j+k]=x+y; 33 a[j+k+i]=x-y; 34 w=w*wi; 35 } 36 } 37 } 38 if (f==-1) 39 for (int i=0; i<n; i++){ 40 a[i].x/=n; a[i].y/=n; 41 } 42 } 43 int main() 44 { 45 int n,m; 46 scanf("%d%d",&n,&m); n++; m++; 47 for (int i=0; i<n; i++) scanf("%lf",&a[i].x); 48 for (int i=0; i<m; i++) scanf("%lf",&b[i].x); 49 int l=0,N=1; 50 while (N<n+m-1) N<<=1,l++; 51 fft(a,N,l,1); 52 fft(b,N,l,1); 53 for (int i=0; i<N; i++) c[i]=a[i]*b[i]; 54 fft(c,N,l,-1); 55 for (int i=0; i<n+m-1; i++) printf("%d ",(int)(c[i].x+0.5)); 56 return 0; 57 }
鸣谢:LLX大佬
(Ps:一个巨搞笑的东西:传送门)