最小二乘法

（一）正交集与正交基

如果，S中任何两个不同的向量都正交，那么，S称为正交向量集。

如果S是正交向量集 并且是 线性无关集，那么S是正交集。

证明：

同理，所有的ci都是0，所以S是线性无关集。

上述证明思路在下文中会经常使用，故称之为证明方法1.

 

（二）正交投影

假设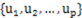是Rⁿ子空间W的正交基，对W中的每个向量y，有线性组合：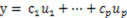

利用证明方法1，可以得到：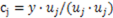

 

向量在向量上的正交投影。

一个向量y可以分解为两个向量之和：一个向量是u的数量乘积，一个向量与u垂直。

 

向量在空间上的正交投影。

 

单位正交基

正交基中我的向量长度都为1.

一个m×n矩阵U具有单位正交列向量的充分必要条件是U^TU=I。

有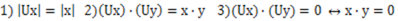：其中性质1）和2）表明线性映射U保持了向量的长度和正交性。

 

结合上述知识，我们可以得到：

如果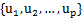是单位正交基，那么

 

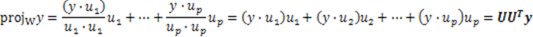
也即：

若U是n×p列单位正交矩阵

如果U是n×n方阵，那么y的投影依然是y。

 

（三）普通基转化为正交基：格拉姆-施密特方法

 

（四）QR分解

如果m×n矩阵A的列线性无关，那么A可以分解为A=QR，其中Q是一个m×n矩阵，Q的列形成ColA的标准正交基（即：单位正交基），R是一个n×n上三角可逆矩阵且对角线上的元素为正数。

 

（五）最小二乘法

Question：Ax=b。寻找最优的x。

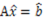
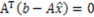
（称之为Ax=b的法方程）

如果A是线性无关列，那么可以对A进行QR分解。得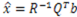

 

扩展加权最小二乘法