实用的空间几何方法
实用的空间几何方法
设点表示为 P (x,y,z)，直线表示为过点P (x,y,z) 和方向direction (x,y,z)，平面表示为过点P (x,y,z) 和法线方向norm (x,y,z)。
代数符号 * 表示向量点积， \(\cdot\) 表示向量叉积，||表示向量模长，normalize()表示求单位向量。
1 向量法求直线和平面交点
过点P和方向为L的直线，与过点Q和法线方向为N的平面的交点M。
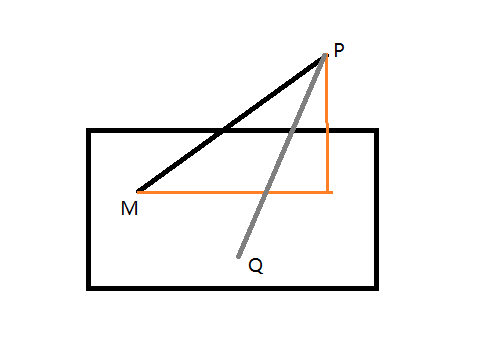
过P点的直线在平面法向上的投影都相等，因此可以得到：
\[PM*norm=PQ*norm
\]
已知P、Q两点坐标，向量PQ可以求到。另外知道直线PM方向向量L，则M点可表示为：
\[M=P+t*L
\]
代入上式可得：
\[(P+t*L-P)*norm=(Q-P)*norm
\]
\[t=\frac{(Q-P)*norm}{L*norm}
\]
2 向量法求两平面交线
过点P和法线方向为M的平面，与过点Q和法线方向为N的平面的交线，设交线过点L，方向向量为A。
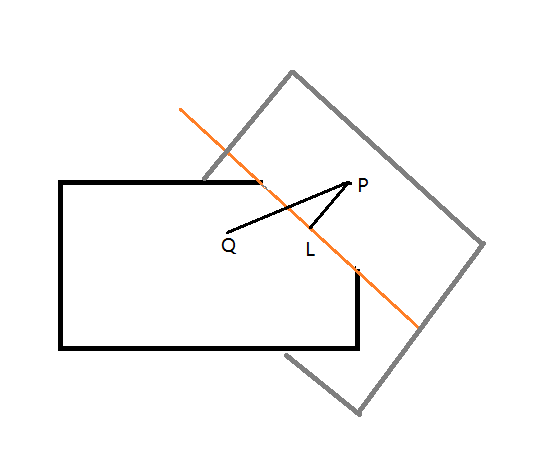
首先可以通过平面法向量M、N求得直线方向向量：
\[A=M\cdot N
\]
然后通过A和法向量M可以求到直线PL的方向向量：
\[PL=M\cdot A
\]
于是问题转变为求直线PL和过点Q和法线方向为N的平面的交点。如第一章所述，可以求得：
\[L=P+t*PL
\]
\[t=\frac{(Q-P)*N}{PL*N}
\]
3 向量法求两直线交点
过点P和方向为A的直线，与过点Q和方向为B的直线的交点设为M。
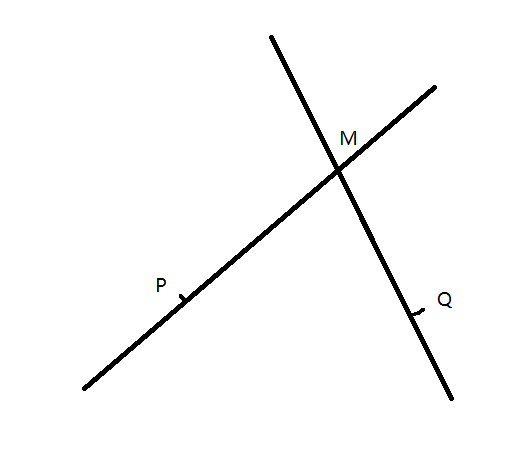
已知：
\[M=P+t1*A
\]
\[M=Q+t2*B
\]
\[MQ\cdot B=0
\]
代入化简可得：
\[(M-Q)\cdot B=0
\]
\[(P+t1*A-Q)\cdot B=0
\]
\[(P-Q)\cdot B-t1*A\cdot B=0
\]
\[t1=\frac{|(P-Q)\cdot B|}{|A\cdot B|}
\]
4 向量法求三角形外接圆
已知点A、B、C围成的三角形，求三角形的外接圆圆心O。
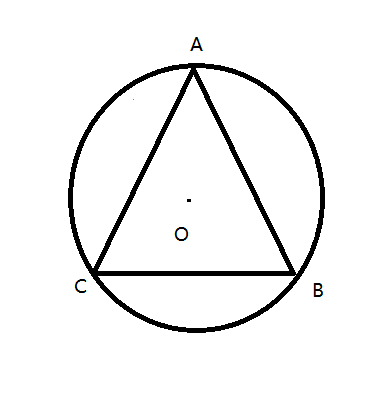
因为：
\[向量 AB=A-B
\]
\[ 向量 BC=B-C
\]
\[norm=AB\cdot BC
\]
得到：
\[O=A+\frac{AB\cdot BC\cdot AB*|BC|^2+BC\cdot AB\cdot BC*|BC|^2}{2*|norm|^2}
\]
5 根据TrackBall求旋转矩阵
如图所示，屏幕上有一个半球，因为鼠标为屏幕坐标系，想要通过鼠标实现对三维世界物体的旋转，可以参考trackball的方式获取到。
auto calScreenZ=[](float r, float x,float y){
float d,t,z;
d=sqrt(x*x+y*y);
//Inside sphere
if(d<r*0.707)
{
z=sqrt(r*r-d*d);
}
//On hyperbola
else
{
t=r/1.41421;
z=t*t/d;
}
return z;
};
///获取归一化屏幕坐标
osg::Vec3 p1={2.0*(x1-xmin)/(xmax-xmin)-1.0,2.0*(y1-ymin)/(ymax-ymin)-1.0};
osg::Vec3 p2={2.0*(x2-xmin)/(xmax-xmin)-1.0,2.0*(y2-ymin)/(ymax-ymin)-1.0};
p1.z()=calScreenZ(_trackballSize,p1.x(),p1.y());
p2.z()=calScreenZ(_trackballSize,p2.x(),p2.y());
///获取相机旋转矩阵
auto viewMat=getCameraViewMat().getRotate();
p1=p1*osg::Matrix::inverse(viewMat);
p2=p2*osg::Matrix::inverse(viewMat);
///计算旋转矩阵
osg::Quat localQuat;
localQuat.makeRotate(p2,p1);
