数据结构与算法 | 1.数据结构与算法初探
博客内容为 浙江大学:陈越姥姥 的教学视频笔记
一、什么是数据结构
数据结构是计算机中存储、组织数据的方式。通常情况下,精心选择的数据结构可以带来最优效率的算法。
1.通过小例子理解——“摆放图书”
(1)问题描述
- 现在给到一堆图书以及一些书架,怎么将图书摆放到书架上面去呢???
- 图书摆放时需要考虑到的两个方面:
- a.新书怎么放到书架上面呢?
- b.怎么找到指定的图书呢?
(2)三种解决方案
- 第一种解决方案:随便放
- a.放置新书时,哪里有位置就放在哪里。
- b.找指定新书时,从头到尾开始查找。累死...
- 第二种解决方案:按照书名的拼音字母顺序摆放
- a.放置新书时。买了一本《阿Q正传》,那么需要把所有的书往后错位,然后才能把这本字母a开头的书放在指定位置。累死...
- b.查找指定的书时,按照字母顺序,进行二分查找。
- 第三种解决方案:将书和书架按照类别区分,在每个类别中再按照英文字母顺序摆放
- a.放置新书时,先确定类别,再二分查找到相应位置移出空位。
- b.查找指定的书时,先找到类别,再二分查找。
(3)由“摆放图书”引出来的问题
----> 空间要如何分配???类型应该分多细???
2.逻辑结构与存储结构
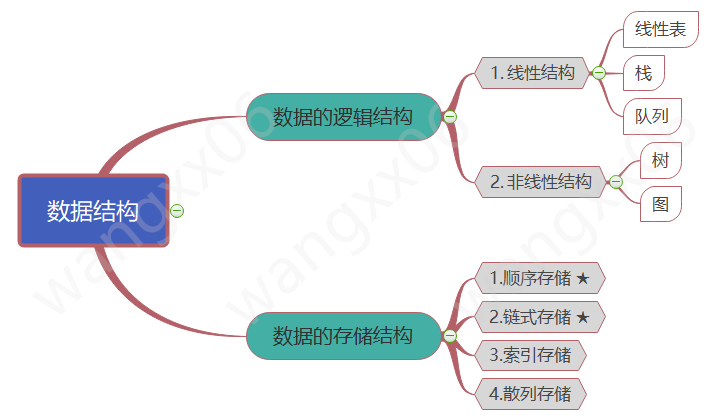
(1)逻辑结构
逻辑结构:是指数据对象中数据元素之间的相互关系。主要分为以下四类:

- a.集合结构
- 集合结构中的数据元素除了同属一个集合外,它们之间没有其他关系。
- b.线性结构
- 线性结构中的数据元素之间是一对一的关系。
- c.树形结构
- 树形结构中的数据元素之间存在一对多的层次关系。
- d.图形结构
- 图形结构的数据元素是多对多的关系。
(2)存储结构
存储结构:是指数据的逻辑结构在计算机中的存储形式。数据元素之间的关系在计算机中有两种不同的表示方法:顺序映像和非顺序映像,由此得到两种不同的存储结构:顺序存储结构和链式存储结构。

- 顺序存储结构
- 把数据元素放在地址连续的存储单元里,其数据间的逻辑关系与物理关系是一致的。
- 链式存储结构
- 把数据元素存放在任意的存储单元里,这组存储单元可以是连续的、也可以是不连续的。
- 数据元素间的存储关系不能反映其逻辑关系,因此需要使用指针存放数据元素的地址,这样通过地址可以找到相关联数据元素的位置。
- 例子说明两种存储结构
- 考试时:考场共30个座位,30位考生按照1~30的编号依次按照顺序落座,可以根据座位知道是哪位编号的学生。
- 上课时:教室30个座位,学生按照1~30编号。在教室内随便坐,但是只有编号相邻的同学知道相互的位置在哪。
3.抽象数据类型(Abstract Data Type)
抽象数据类型(简称ADT),是指一个数学模型以及定义在该模型上的一组操作。
抽象数据类型的定义仅取决于它的一组逻辑特性,而与其在计算机内部如何表示和实现无关。即不管内部结构如何,只要数学结构不改变,都不影响其外部的使用。
(1)什么是抽象数据类型
- 数据类型
- 数据对象集
- 数据集合相关联的操作集
- 抽象:描述数据类型的方法不依赖于具体实现
- 与存放数据的机器无关
- 与数据存储的物理结构无关
- 与实现操作的算法和编程语言均无关
- 抽象数据类型的三元组表示
- 抽象数据类型的三元组表示为:(D,S,P)
- 其中,D是数据对象,S是D上的关系集,P是对D的基本操作集。
(2)抽象数据类型的格式化定义
- 抽象数据类型的格式化定义:
ADT 抽象数据类型名{ 数据对象:<数据对象的定义> 数据关系:<数据关系的定义> 基本操作:<基本操作的定义> }ADT 抽象数据类型名 // 其中,数据对象和数据关系的定义用伪代码描述,基本操作的定义格式为 基本操作名(参数表) 初始条件:<初始条件描述> 操作结果:<操作结果描述>
二、什么是算法
算法是解决特性问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
// 问题:解决 1 + 2 + 3 + ... + 100 的计算问题。两种算法实现
// 算法1:循环相加
int i, sum = 0, n = 100;
for(i = 1; i <= n; i++){
sum = sum + i;
}
printf(" %d ", sum);
// 算法2:求和公式
int i, sum = 0, n = 100;
sum = (1 + n) * n / 2;
printf(" %d ", sum);
1.算法的定义
- 算法:(Algorithm)
- 一个有限指令集
- 接受一些输入(有些情况下不需要输入)
- 产生输出
- 一定在有限步骤之后终止
- 每一条指令必须:
- 有充分明确的目标,不可以有歧义
- 计算机能处理的范围之内
- 描述应不依赖于任何一种计算机语言以及具体的实现手段
2.算法的特性和设计要求
(1)算法的5个特性
- a.有穷性
- 一个算法必须总是在执行有穷步之后结束,且每一个步骤都在有穷的时间内完成。
- b.确定性
- 算法中的每一条指令必须有明确的含义,读者理解时不会产生二义性。并且,任何条件下,相同的输入只能得出相同的输出。
- c.可行性
- 算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现的。
- d.输入
- 一个算法可以有零个或者多个输入。
- e.输出
- 一个算法可以有一个或者多个输出。
(2)算法的设计要求
- a.正确性
- 算法应当满足具体问题的需求。
- “正确”的四个层次
- 第一层:算法程序没有语法错误
- 第二层:算法程序对于合法的输入数据能够产生满足要求的输出结果
- 第三层:算法程序对于非法的输入数据能够得出满足规格说明的结果
- 第四层:算法程序对于精心选择的,甚至于***难的测试数据都有满足要求的输出结果
- b.可读性
- 算法主要是为了人的阅读与交流,其次才是计算机的执行。可读性强有助于读者理解、调试和修改。
- c.健壮性
- 当输入非法数据时,算法也能做相应的处理,而不是产生异常或莫名其妙的结束。
- d.效率与低存储量的需求
- 效率:算法执行的时间,执行时间短的算法效率高。
- 存储量:算法执行中需要多大内存。
3.算法的度量方法(空间和时间)
(1)什么是好的算法
- 空间复杂度S(n)
- 根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限,导致程序非正常中断。
- 时间复杂度T(n)
- 根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行的结果。
(2)算法的存储空间需求——空间复杂度
-
关于空间复杂度的算法示例:
// 问题:打印1到N的全部正整数。两种算法实现 // 算法1:for循环实现 void PrintN ( int N ) { int i; for ( i=1; i<=N; i++ ){ printf("%d\n", i ); } return; } //算法2:递归实现 void PrintN ( int N ) { if ( N ){ PrintN( N - 1 ); printf("%d\n", N ); } return; } /* 结果展示: 分别令 N = 100, 1000, 10000, 10000, ...... for循环模式:不管N等于多大,都可以打印出来。 递归模式:当N大到一定程度时,程序爆掉,直接跳出程序。 结果分析: 递归占用内存空间较大,输入规模变大时,导致爆栈(递归依赖于 栈 来实现)*/ -
空间复杂度
- 空间复杂度(space complexity)作为算法所需存储空间的量度,记作: S(n) = O(f(n)) ;其中,n是问题规模的大小。
(3)算法效率的度量——时间复杂度
-
关于时间复杂度的算法示例:
问题:一元多项式f(x)=a0 + a1x + ... + an-1xn-1 + anxn, 求x在某一点处的取值。// 问题:计算一元多项式在给定点x处的取值。两种算法 // 算法1:小白程序员 double f( int n, double a[], double x ){ int i; double p = a[0]; for( i=1; i<=n; i++ ) p += (a[i] * pow(x, i)); // 在每个循环内部,执行了 i次 乘法运算。 return p; } // 算法2:正常程序员 double f( int n, double a[], double x){ int i; double p = a[n]; for( i=n, i>0, i--) p = a[i-1] + x*p; //在每个循环内部,只执行了 1次 乘法运算。 return p; } /* 结果展示: 分别赋值进行计算,并各自循环 1e7 次,查看两个程序执行的快慢情况。 算法2 明显消耗时间比 算法1 要短。 结果分析: 乘除 比 加减 更加消耗时间,而 算法1 中的乘除次数明显比 算法2 中的乘除次数多。因此 算法2 的算法效率更高。*/- 关于两种算法的分析:
- 第一种算法,直接按照公式编写代码,公式为:f(x)=a0 + a1x + ... + an-1xn-1 + anxn
- 第二种算法,将公式变形后编写代码,变形后的公式为:f(x)=a0 + x(a1 + x(a2 + x(...x(an-1 + x(an))...)))
- 第一种算法中,在每个循环内部,执行了 i次 乘法运算,共循环 n次,因此整个程序执行 1 + 2 + 3 + ... + n = n(n+1)/2 次乘法运算。
- 第二种算法中,在每个循环内部,只执行了 1次 乘法运算,共循环 n次,因此整个程序执行 n次 乘法运算。
- ---->因此,第二种算法的算法效率更高。
- 关于两种算法的分析:
(4)复杂度的渐进表示
当我们在分析算法复杂度时,没有必要一步一步地去数把每个操作做了多少次。我们关心的只是:随着要处理的数据的规模的增大,复杂度增长的性质。
在上述“时间复杂度的算法例子”中,只需要知道 算法1 是 n2 在起主要作用,而 算法2 是 n 在起主要作用。当 n 变大时,算法1 比 算法2 耗时更大即可。
- 推导大O阶方法
- 用常数1取代运行时间中的所有加法常数;
- 在修改后的运行次数中,只保留最高阶项;
- 如果最高阶项存在且不是1,则去除与这个项相乘的常数。
- 推导大O阶的几个例子:
- O(1)阶例子
注意:是O(1)而不是O(3)int i, sum = 0, n = 100; sum = (1 + n) * n / 2; printf(" %d ", sum); - O(n)阶例子
int i; for(i = 1; i <= n; i++){ printf(" %d ", i); } - O(n2)阶例子
// 例子1:j循环时的初始值为1 int i,j; for(i = 1; i <= n; i++){ for(j = 1; j <= n; j++){ printf(" %d ", i); } } // 例子2:j循环时的初始值是i int i,j; for(i = 1; i <= n; i++){ for(j = i; j <= n; j++){ printf(" %d ", i); } }- 例子1分析:两层循环,各自循环n次,总的执行次数是 n + n + ... + n = n * n = n2,因此时间复杂度是O(n2)
- 例子2分析:两层循环,外层循环n次,内层循环(n-i)次,因此总的执行次数是 n + (n - 1) + (n - 2) + ... + 2 + 1 = n(n + 1)/2 = n2/2 + n/2。只保留最高阶并去除最高阶系数,得到时间复杂度为O(n2)
- O(logn)阶例子
int count = 1; whie(count < 2){ count = count * 2; }- 例子分析:每次循环count都乘以2,因此当 2x >= n 时,退出循环。得到执行次数 x = log2n。时间复杂度即为O(logn)
- O(1)阶例子
常用复杂度的表示
-
常用的复杂度
阶 O(1) O(logn) O(n) O(nlogn) O(nsup>2) O(nsup>3 2n n! -
函数、输入规模n、复杂度的图标
-
每秒钟10亿指令计算机的运行时间表
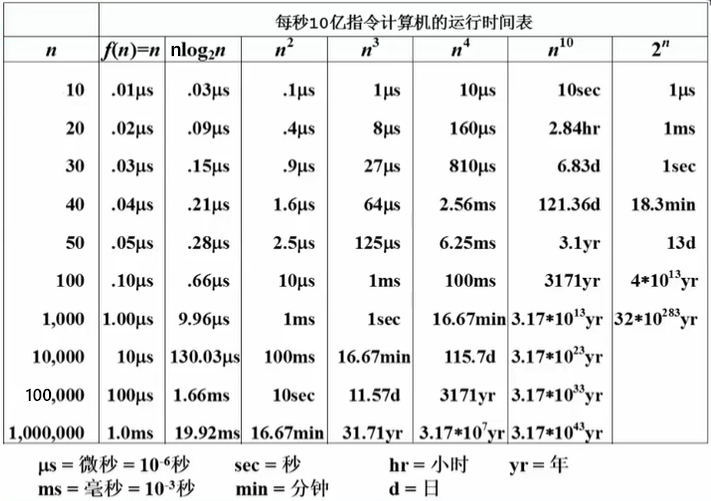
- 因此,越小的复杂度越好。
-
复杂度分析小窍门
- 如果两段算法分别有复杂度T1(n)=O(f1(n))和T2(n)=O(f2(n)),则:
- T1(n) + T2(n) = max( O(f1(n)), O(f2(n)) )
- T1(n) * T2(n) = O( f1(n) * f2(n) )
- 若T(n)是关于n的k阶多项式,那么T(n)=O(nk)
- 一个for循环的时间复杂度等于 循环次数 乘以 循环体代码的复杂度。
- if-else结构的复杂度取决于if的条件判断复杂度和两个分支部分的复杂度,总体复杂度取三者中最大。
- 如果两段算法分别有复杂度T1(n)=O(f1(n))和T2(n)=O(f2(n)),则:
三、通过“最大子列和”看算法优化问题
问题:给定N个整数的序列 {A1,A2,...,AN},求最大子列和。
1.算法1
(1)算法1的逻辑思考
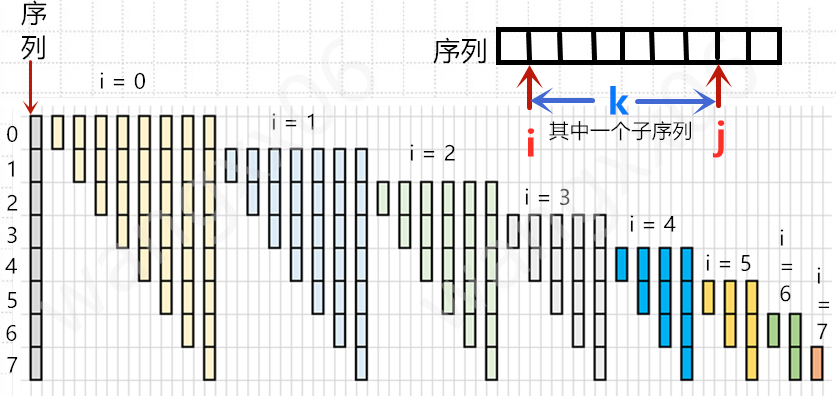
- 要计算子列,则需要考虑三部分内容,子列左端、子列右端、子列的和。
- 子列的左端为i, 它的取值范围是[0,N]
- 子列的右端为j,它的取值范围是[i,N]
- 子列的和ThisSum,它计算的范围是[i,j],通过变量k循环遍历取值求和。
- 这种方法用图片表示为:
(2)算法1代码实现
- 算法1代码实现:
int MaxSubseqSum1(int A[], int N){ int ThisSum, MaxSum = 0; for(i = 0; i < N; i++){ // i是子序列的左端位置 for(j = i; j < N; j++){ // j是子序列的右端位置 ThisSum = 0; // ThisSum是从A[i]到A[j]的子列和 for(k = i; k <= j; k++) ThisSum += A[k]; // 循环遍历求和 if(ThisSum > MaxSum) // 如果刚得到的子列和更大,则更新最大子列和的值 MaxSum = ThisSum; } // j循环结束 } // i循环结束 return MaxSum; } - 算法1分析:
- 使用了三重for循环的嵌套。最内层的时间复杂度为O(1),在第一层循环共循环了j-i次;第二层循环了N-i次;第外层循环了N次。时间复杂度为T(N)=O(N3)
2.算法2
(1)算法2的逻辑思考
- 算法2主要是算法1的改进!!!
- 在算法1中,当 i = 1 ,N = 8 时:
- j = 1 时,ThisSum = A[1];判断(ThisSum > MaxSum) ;清零ThisSum = 0。
- j = 2 时,ThisSum = A[1] + A[2];判断(ThisSum > MaxSum) ;清零ThisSum = 0。
- j = 3 时,ThisSum = A[1] + A[2] + A[3];判断(ThisSum > MaxSum) ;清零ThisSum = 0。
- j = 4 时,ThisSum = A[1] + A[2] + A[3] + A[4];判断(ThisSum > MaxSum) ;清零ThisSum = 0。
- j = 5 时,ThisSum = A[1] + A[2] + A[3] + A[4] + A[5];判断(ThisSum > MaxSum) ;清零ThisSum = 0。
- j = 6 时,ThisSum = A[1] + A[2] + A[3] + A[4] + A[5] + A[6];判断(ThisSum > MaxSum) ;清零ThisSum = 0。
- j = 7 时,ThisSum = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7];判断(ThisSum > MaxSum) ;清零ThisSum = 0。
- 每次ThisSum都需要从 A[i] 开始,一直累加到 A[j]。可以看到做了很大的重复性工作。
- 改进方案:保存ThisSum的值,每次只需要重新加上下一个数据元素即可。
- 在算法2中的改进:ThisSum在最外层循环才执行清零操作。当 i = 1 ,N = 8 时:
- j = 1 时,ThisSum = A[1];判断(ThisSum > MaxSum);此时ThisSum = A[1]。
- j = 2 时,ThisSum = ThisSum + A[2];判断(ThisSum > MaxSum);此时ThisSum = A[1] + A[2]。
- j = 3 时,ThisSum = ThisSum + A[3];判断(ThisSum > MaxSum);此时ThisSum = A[1] + A[2] + A[3]。
- j = 4 时,ThisSum = ThisSum + A[4];判断(ThisSum > MaxSum);此时ThisSum = A[1] + A[2] + A[3] + A[4]。
- j = 5 时,ThisSum = ThisSum + A[5];判断(ThisSum > MaxSum);此时ThisSum = A[1] + A[2] + A[3] + A[4] + A[5]。
- j = 6 时,ThisSum = ThisSum + A[6];判断(ThisSum > MaxSum);此时ThisSum = A[1] + A[2] + A[3] + A[4] + A[5] + A[6]。
- j = 7 时,ThisSum = ThisSum + A[7];判断(ThisSum > MaxSum);此时ThisSum = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7]。
- 然后跳出第二层for循环,i自增为2,将ThisSum清零,再进入循环体。
- 在算法1中,当 i = 1 ,N = 8 时:
(2)算法2代码实现
-
算法2代码实现:
int MaxSubseqSum2(int A[], int N){ int i,j; for(i = 0; i <N; i++){ // i是子列左端位置 ThisSum = 0; // ThisSum是从A[i]到A[j]的子列和 for(j = i; j < N; j++){ // j是子列的右端位置 ThisSum += A[j]; //对于相同的i,不同的j,只需要在j-1次循环的基础上累加1项即可。 if(ThisSum > MaxSum) // 如果刚得到的这个子列和更大。则更新结果 MaxSum = ThisSum; } // j循环结束 } // i循环结束 return MaxSum; } -
算法2分析:
- 算法2共使用了两层循环。最内层的时间复杂度为O(1),第一层循环次数为N-i,最外层循环次数为N。因此时间复杂度为O(n2)
3.算法3——分而治之
(1)算法3的逻辑思考
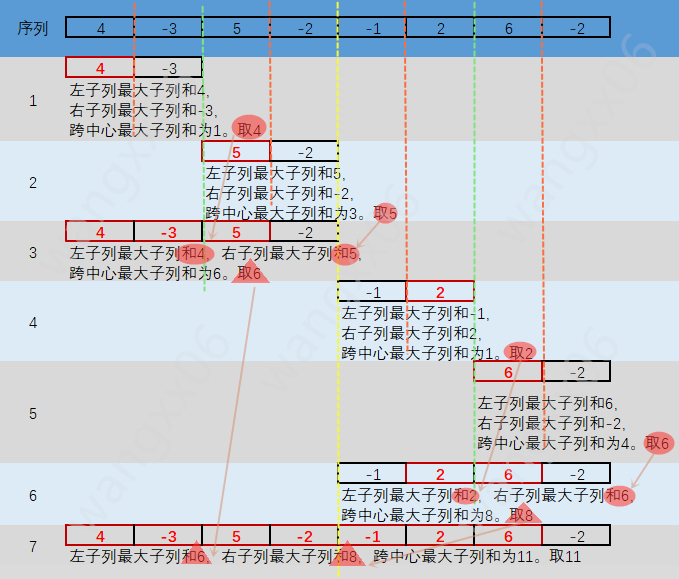
为了方便理解,在这里假定整数序列为{4,-3,5,-2,-1,2,6,-2}
- 分治的核心思想——“分”和“治”
- 分:将序列从中间一分为二,找出左子列的最大子列和Max左;找出右子列的最大子列和Max右;再找到跨中心的最大子列和Max中
- 治:比较Max左、Max右、Max中,最大子列和必是其中最大者。
- 借助“递归”的思想,可以把左子列、右子列继续分治下去。
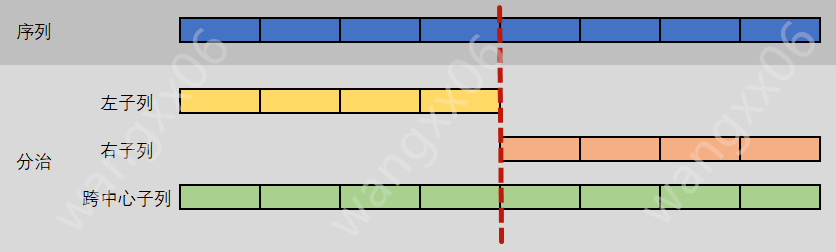
- 当假定整数序列为{4,-3,5,-2,-1,2,6,-2}时,说明分治的方法。
(2)算法3代码实现
-
算法3代码实现:
// C语言年就不用...我写不出来。自行搜索答案。以后将在其他专栏使用Python及Java编写此算法的代码。 -
关于算法3的分析
- 这部分我刚开始很迷,不懂。因此当我推导出结果之后,就写的极其详细。

4.算法4——在线处理
(1)算法4的逻辑思考
- 在线处理——时间复杂度降到了最低
- 步骤一:从子列的第一个元素开始读,并将其赋值给ThisSum。执行下一步。
- 步骤二:读取下一个元素,然后把这个元素的值与ThisSum相加。执行下一步。
- 步骤三:判断ThisSum的值和MaxSum的值,如果ThisSum > MaxSum,则赋值MaxSum = ThisSum 。执行下一步。
- 步骤四:判断ThisSum的值是否小于0,如果小于0,则将ThisSum的值清0;如果不小于0,则继续跳到步骤二并顺序执行。(因为如果ThisSum小于0,则会使后面的子列和减小)
- 步骤五:循环结束,输出最大子列和MaxSum。
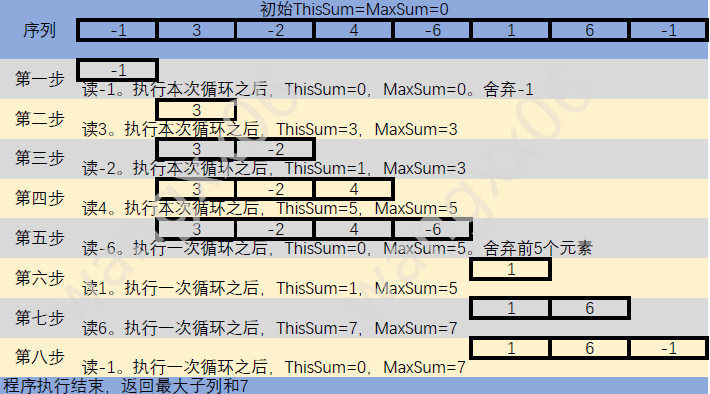
- 以序列{-1,3,-2,4,-6,1,6,-1}为例子,使用图片说明
(2)算法4代码实现
-
算法4代码实现:
int MaxSubseqSum4{ int ThisSum, MaxSum; int i; for(i = 0; i < N; i++){ ThisSum += A[i]; // 向右累加 if(ThisSum > MaxSum) MaxSum = ThisSum; // 发现更大和时,更新当前结果 else if(ThisSum < 0) // 如果当前子列和为负,则不可能使后面的部分增大,故抛弃 ThisSum = 0; } return MaxSum; } -
关于算法4的分析
- 只执行了一层循环,每层循环内执行的时间为常数,因此循环内每执行一次的时间复杂度为O(1)。由于循环,因此整个算法的时间复杂度为O(n)。
- 假如只查看序列中的值,尚且需要时间复杂度O(n);因此,在线处理是解决“最大子列和”的最优算法(时间复杂度最低)。
内容原创,请注明出处。如有错误,希望您在评论区指出。