CS231n 2016 通关 第三章-Softmax 作业
在完成SVM作业的基础上,Softmax的作业相对比较轻松。
完成本作业需要熟悉与掌握的知识:

cell 1 设置绘图默认参数
1 mport random 2 import numpy as np 3 from cs231n.data_utils import load_CIFAR10 4 import matplotlib.pyplot as plt 5 %matplotlib inline 6 plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots 7 plt.rcParams['image.interpolation'] = 'nearest' 8 plt.rcParams['image.cmap'] = 'gray' 9 10 # for auto-reloading extenrnal modules 11 # see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython 12 %load_ext autoreload 13 %autoreload 2
cell 2 读取数据,并显示各个数据的尺寸:
1 def get_CIFAR10_data(num_training=49000, num_validation=1000, num_test=1000, num_dev=500): 2 """ 3 Load the CIFAR-10 dataset from disk and perform preprocessing to prepare 4 it for the linear classifier. These are the same steps as we used for the 5 SVM, but condensed to a single function. 6 """ 7 # Load the raw CIFAR-10 data 8 cifar10_dir = 'cs231n/datasets/cifar-10-batches-py' 9 X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir) 10 11 # subsample the data 12 mask = range(num_training, num_training + num_validation) 13 X_val = X_train[mask] 14 y_val = y_train[mask] 15 mask = range(num_training) 16 X_train = X_train[mask] 17 y_train = y_train[mask] 18 mask = range(num_test) 19 X_test = X_test[mask] 20 y_test = y_test[mask] 21 mask = np.random.choice(num_training, num_dev, replace=False) 22 X_dev = X_train[mask] 23 y_dev = y_train[mask] 24 25 # Preprocessing: reshape the image data into rows 26 X_train = np.reshape(X_train, (X_train.shape[0], -1)) 27 X_val = np.reshape(X_val, (X_val.shape[0], -1)) 28 X_test = np.reshape(X_test, (X_test.shape[0], -1)) 29 X_dev = np.reshape(X_dev, (X_dev.shape[0], -1)) 30 31 # Normalize the data: subtract the mean image 32 mean_image = np.mean(X_train, axis = 0) 33 X_train -= mean_image 34 X_val -= mean_image 35 X_test -= mean_image 36 X_dev -= mean_image 37 38 # add bias dimension and transform into columns 39 X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))]) 40 X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))]) 41 X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))]) 42 X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))]) 43 44 return X_train, y_train, X_val, y_val, X_test, y_test, X_dev, y_dev 45 46 47 # Invoke the above function to get our data. 48 X_train, y_train, X_val, y_val, X_test, y_test, X_dev, y_dev = get_CIFAR10_data() 49 print 'Train data shape: ', X_train.shape 50 print 'Train labels shape: ', y_train.shape 51 print 'Validation data shape: ', X_val.shape 52 print 'Validation labels shape: ', y_val.shape 53 print 'Test data shape: ', X_test.shape 54 print 'Test labels shape: ', y_test.shape 55 print 'dev data shape: ', X_dev.shape 56 print 'dev labels shape: ', y_dev.shape
数据维度结果:

cell 3 用for循环实现Softmax的loss function 与grad:
1 # First implement the naive softmax loss function with nested loops. 2 # Open the file cs231n/classifiers/softmax.py and implement the 3 # softmax_loss_naive function. 4 5 from cs231n.classifiers.softmax import softmax_loss_naive 6 import time 7 8 # Generate a random softmax weight matrix and use it to compute the loss. 9 W = np.random.randn(3073, 10) * 0.0001 10 loss, grad = softmax_loss_naive(W, X_dev, y_dev, 0.0) 11 12 # As a rough sanity check, our loss should be something close to -log(0.1). 13 print 'loss: %f' % loss 14 print 'sanity check: %f' % (-np.log(0.1))
对应的py文件的代码:
1 def softmax_loss_naive(W, X, y, reg): 2 """ 3 Softmax loss function, naive implementation (with loops) 4 5 Inputs have dimension D, there are C classes, and we operate on minibatches 6 of N examples. 7 8 Inputs: 9 - W: A numpy array of shape (D, C) containing weights. 10 - X: A numpy array of shape (N, D) containing a minibatch of data. 11 - y: A numpy array of shape (N,) containing training labels; y[i] = c means 12 that X[i] has label c, where 0 <= c < C. 13 - reg: (float) regularization strength 14 15 Returns a tuple of: 16 - loss as single float 17 - gradient with respect to weights W; an array of same shape as W 18 """ 19 # Initialize the loss and gradient to zero. 20 loss = 0.0 21 dW = np.zeros_like(W) 22 23 ############################################################################# 24 # TODO: Compute the softmax loss and its gradient using explicit loops. # 25 # Store the loss in loss and the gradient in dW. If you are not careful # 26 # here, it is easy to run into numeric instability. Don't forget the # 27 # regularization! # 28 ############################################################################# 29 num_calss = W.shape[1] 30 num_train = X.shape[0] 31 buf_e = np.zeros(num_calss) 32 #print buf_e.shape 33 34 for i in xrange(num_train) : 35 for j in xrange(num_calss) : 36 #1*3073 * 3073*1 = 1 >>>10 37 buf_e[j] = np.dot(X[i,:],W[:,j]) 38 buf_e -= np.max(buf_e) 39 buf_e = np.exp(buf_e) 40 buf_sum = np.sum(buf_e) 41 buf = buf_e/ buf_sum 42 loss -= np.log(buf[y[i]] ) 43 for j in xrange(num_calss): 44 dW[:,j] +=( buf[j] - (j ==y[i]) )*X[i,:].T 45 #regularization with elementwise production 46 loss /= num_train 47 dW /= num_train 48 49 loss += 0.5 * reg * np.sum(W * W) 50 dW +=reg*W 51 #gradient 52 53 ############################################################################# 54 # END OF YOUR CODE # 55 ############################################################################# 56 57 return loss, dW
计算得到的结果:

使用了课程上所讲的验证方式。
问题:
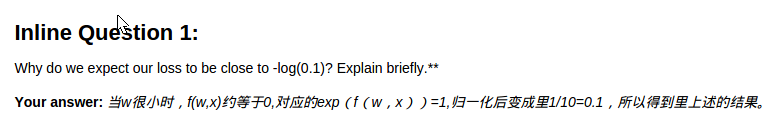
cell 4 使用数值计算法对解析法得到的grad进行检验:
1 # Complete the implementation of softmax_loss_naive and implement a (naive) 2 # version of the gradient that uses nested loops. 3 loss, grad = softmax_loss_naive(W, X_dev, y_dev, 0.0) 4 5 # As we did for the SVM, use numeric gradient checking as a debugging tool. 6 # The numeric gradient should be close to the analytic gradient. 7 from cs231n.gradient_check import grad_check_sparse 8 f = lambda w: softmax_loss_naive(w, X_dev, y_dev, 0.0)[0] 9 grad_numerical = grad_check_sparse(f, W, grad, 10) 10 11 # similar to SVM case, do another gradient check with regularization 12 loss, grad = softmax_loss_naive(W, X_dev, y_dev, 1e2) 13 f = lambda w: softmax_loss_naive(w, X_dev, y_dev, 1e2)[0] 14 grad_numerical = grad_check_sparse(f, W, grad, 10)
计算结果:

cell 5 使用向量法来实现loss funvtion与grad,并与使用for循环法比较:
1 # Now that we have a naive implementation of the softmax loss function and its gradient, 2 # implement a vectorized version in softmax_loss_vectorized. 3 # The two versions should compute the same results, but the vectorized version should be 4 # much faster. 5 tic = time.time() 6 loss_naive, grad_naive = softmax_loss_naive(W, X_dev, y_dev, 0.00001) 7 toc = time.time() 8 print 'naive loss: %e computed in %fs' % (loss_naive, toc - tic) 9 10 from cs231n.classifiers.softmax import softmax_loss_vectorized 11 tic = time.time() 12 loss_vectorized, grad_vectorized = softmax_loss_vectorized(W, X_dev, y_dev, 0.00001) 13 toc = time.time() 14 print 'vectorized loss: %e computed in %fs' % (loss_vectorized, toc - tic) 15 16 # As we did for the SVM, we use the Frobenius norm to compare the two versions 17 # of the gradient. 18 grad_difference = np.linalg.norm(grad_naive - grad_vectorized, ord='fro') 19 print 'Loss difference: %f' % np.abs(loss_naive - loss_vectorized) 20 print 'Gradient difference: %f' % grad_difference
比较的结果:

向量法的具体代码实现:
1 def softmax_loss_vectorized(W, X, y, reg): 2 """ 3 Softmax loss function, vectorized version. 4 5 Inputs and outputs are the same as softmax_loss_naive. 6 """ 7 # Initialize the loss and gradient to zero. 8 loss = 0.0 9 dW = np.zeros_like(W) 10 num_calss = W.shape[1] 11 num_train = X.shape[0] 12 ############################################################################# 13 # TODO: Compute the softmax loss and its gradient using no explicit loops. # 14 # Store the loss in loss and the gradient in dW. If you are not careful # 15 # here, it is easy to run into numeric instability. Don't forget the # 16 # regularization! # 17 ############################################################################# 18 #500*3073 3073*10 >>>500*10 19 buf_e = np.dot(X,W) 20 # 10 * 500 - 1*500 T 21 buf_e = np.subtract( buf_e.T , np.max(buf_e , axis = 1) ).T 22 buf_e = np.exp(buf_e) 23 #10*500 - 1*500 T 24 buf_e = np.divide( buf_e.T , np.sum(buf_e , axis = 1) ).T 25 #get loss 26 #print buf.shape 27 loss = - np.sum(np.log ( buf_e[np.arange(num_train),y] ) ) 28 #get grad 29 buf_e[np.arange(num_train),y] -= 1 30 # 3073 * 500 * 500*10 31 loss /=num_train + 0.5 * reg * np.sum(W * W) 32 dW = np.dot(X.T,buf_e)/num_train + reg*W 33 34 ############################################################################# 35 # END OF YOUR CODE # 36 ############################################################################# 37 38 return loss, dW
cell 6 使用验证集与训练集做超参数选取:
1 # Use the validation set to tune hyperparameters (regularization strength and 2 # learning rate). You should experiment with different ranges for the learning 3 # rates and regularization strengths; if you are careful you should be able to 4 # get a classification accuracy of over 0.35 on the validation set. 5 from cs231n.classifiers import Softmax 6 results = {} 7 best_val = -1 8 best_softmax = None 9 learning_rates = np.logspace(-10, 10, 10)# [1e-7, 2e-7,3e-7,4e-7,5e-7] 10 regularization_strengths = np.logspace(-3, 6, 10) #[1e4,5e4,1e5,5e5,1e6,5e6,1e7,5e7,1e8] 11 12 ################################################################################ 13 # TODO: # 14 # Use the validation set to set the learning rate and regularization strength. # 15 # This should be identical to the validation that you did for the SVM; save # 16 # the best trained softmax classifer in best_softmax. # 17 ################################################################################ 18 iters = 1500 19 for lr in learning_rates: 20 for rs in regularization_strengths: 21 softmax = Softmax() 22 softmax.train(X_train, y_train, learning_rate=lr, reg=rs, num_iters=iters) 23 y_train_pred = softmax.predict(X_train) 24 accu_train = np.mean(y_train == y_train_pred) 25 y_val_pred = softmax.predict(X_val) 26 accu_val = np.mean(y_val == y_val_pred) 27 28 results[(lr, rs)] = (accu_train, accu_val) 29 30 if best_val < accu_val: 31 best_val = accu_val 32 best_softmax = softmax 33 ################################################################################ 34 # END OF YOUR CODE # 35 ################################################################################ 36 37 # Print out results. 38 for lr, reg in sorted(results): 39 train_accuracy, val_accuracy = results[(lr, reg)] 40 print 'lr %e reg %e train accuracy: %f val accuracy: %f' % ( 41 lr, reg, train_accuracy, val_accuracy) 42 43 print 'best validation accuracy achieved during cross-validation: %f' % best_val
得到较好的结果:

cell 7 选取较好的超参数的模型,对测试集进行测试,计算准确率:
1 # evaluate on test set 2 # Evaluate the best softmax on test set 3 y_test_pred = best_softmax.predict(X_test) 4 test_accuracy = np.mean(y_test == y_test_pred) 5 print 'softmax on raw pixels final test set accuracy: %f' % (test_accuracy, )
结果:0.378
cell 8 可视化w值:
1 # Visualize the learned weights for each class 2 w = best_softmax.W[:-1,:] # strip out the bias 3 w = w.reshape(32, 32, 3, 10) 4 5 w_min, w_max = np.min(w), np.max(w) 6 7 classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'] 8 for i in xrange(10): 9 plt.subplot(2, 5, i + 1) 10 11 # Rescale the weights to be between 0 and 255 12 wimg = 255.0 * (w[:, :, :, i].squeeze() - w_min) / (w_max - w_min) 13 plt.imshow(wimg.astype('uint8')) 14 plt.axis('off') 15 plt.title(classes[i])
结果:

注:在softmax 与svm的超参数选择时,使用了共同的类,以及类中不同的相应的方法。具体的文件内容与注释如下。
附:通关CS231n企鹅群:578975100 validation:DL-CS231n




 浙公网安备 33010602011771号
浙公网安备 33010602011771号