python学习day-13 机器学习-监督学习-回归-简单&多元线性回归
一、线性回归理论知识
1. 介绍:回归(regression) Y变量为连续数值型(continuous numerical variable)
如:房价,人数,降雨量
分类(Classification): Y变量为类别型(categorical variable)
如:颜色类别,电脑品牌,有无信誉
2. 简单线性回归(Simple Linear Regression)
2.1 很多做决定过过程通常是根据两个或者多个变量之间的关系
2.3 回归分析(regression analysis)用来建立方程模拟两个或者多个变量之间如何关联
2.4 被预测的变量叫做:因变量(dependent variable), y, 输出(output)
2.5 被用来进行预测的变量叫做: 自变量(independent variable), x, 输入(input)
3. 简单线性回归介绍
3.1 简单线性回归包含一个自变量(x)和一个因变量(y)
3.2 以上两个变量的关系用一条直线来模拟
3.3 如果包含两个以上的自变量,则称作多元回归分析(multiple regression)
4. 简单线性回归模型
4.1 被用来描述因变量(y)和自变量(X)以及偏差(error)之间关系的方程叫做回归模型
4.2 简单线性回归的模型是:
![]()

其中: 参数 偏差
5. 简单线性回归方程
E(y) = β0+β1x
这个方程对应的图像是一条直线,称作回归线
其中,β0是回归线的截距
β1是回归线的斜率
E(y)是在一个给定x值下y的期望值(均值)
6. 正向线性关系:
反向线性关系:
无关:
7. 估计的简单线性回归方程
ŷ=b0+b1x
这个方程叫做估计线性方程(estimated regression line)
其中,b0是估计线性方程的纵截距
b1是估计线性方程的斜率
ŷ是在自变量x等于一个给定值的时候,y的估计值
8. 线性回归分析流程:
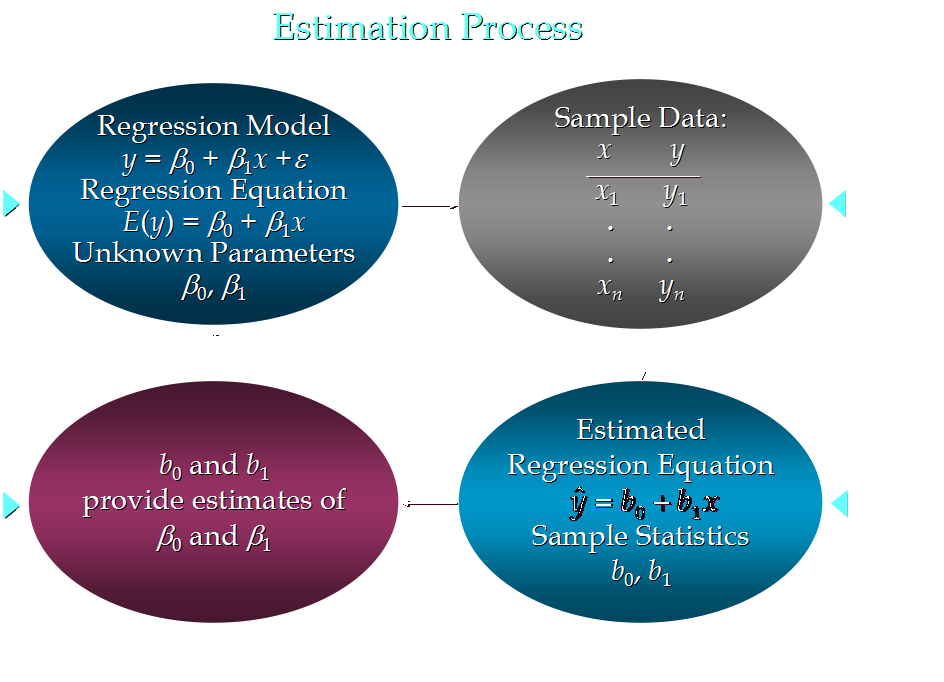
9. 关于偏差ε的假定
11.1 是一个随机的变量,均值为0
11.2 ε的方差(variance)对于所有的自变量x是一样的
11.3 ε的值是独立的
11.4 ε满足正态分布
10
.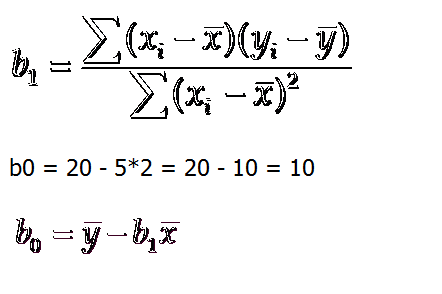
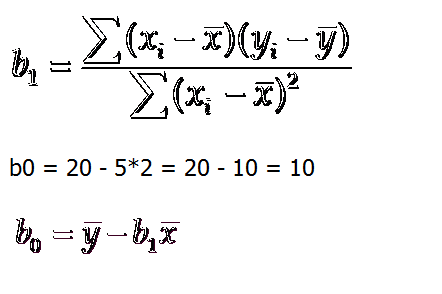
二、线性回归的代码---实际应用

# -*- encoding=utf-8 -*-
#简单现行回归:只有一个自变量 y=k*x+b 预测使 (y-y*)^2 最小
import numpy as np
def fitSLR(x,y):
n=len(x)
dinominator = 0 #分母
numerator=0 #分子
for i in range(0,n):
numerator += (x[i]-np.mean(x))*(y[i]-np.mean(y))
dinominator += (x[i]-np.mean(x))**2
print("numerator:"+str(numerator))
print("dinominator:"+str(dinominator))
b1 = numerator/float(dinominator)
b0 = np.mean(y)/float(np.mean(x))
return b0,b1
# y= b0+x*b1
def prefict(x,b0,b1):
return b0+x*b1
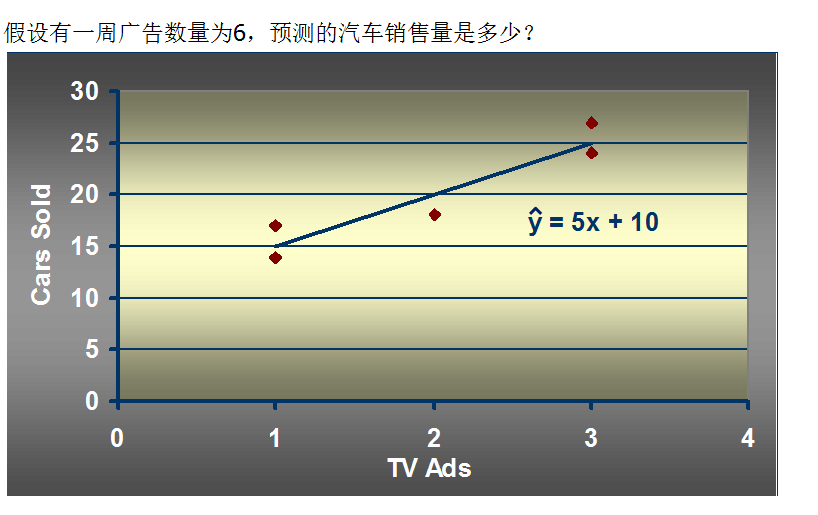
x=[1,3,2,1,3]
y=[14,24,18,17,27]
b0,b1=fitSLR(x, y)
y_predict = prefict(6,b0,b1)
print("y_predict:"+str(y_predict))
输出
三、多元回归理论知识
1. 与简单线性回归区别(simple linear regression)
多个自变量(x)
2. 多元回归模型
y=β0+β1x1+β2x2+ ... +βpxp+ε
其中:β0,β1,β2... βp是参数
ε是误差值
3. 多元回归方程
E(y)=β0+β1x1+β2x2+ ... +βpxp
4. 估计多元回归方程:
y_hat=b0+b1x1+b2x2+ ... +bpxp
一个样本被用来计算β0,β1,β2... βp的点估计b0, b1, b2,..., bp
5. 估计流程 (与简单线性回归类似)
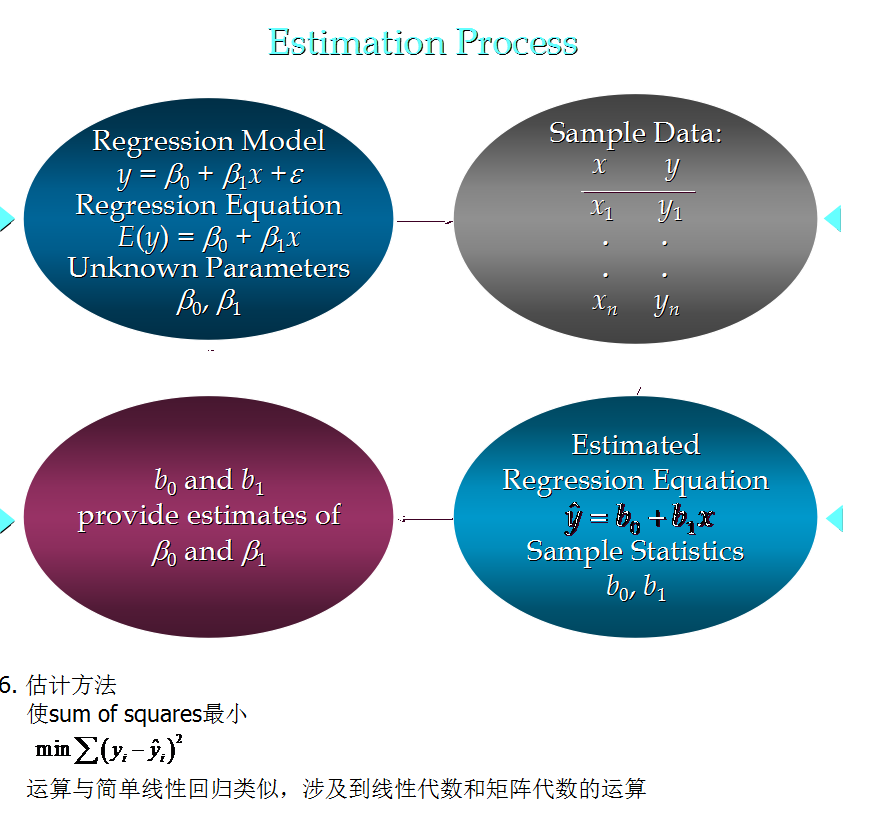
7. 例子
一家快递公司送货:X1: 运输里程 X2: 运输次数 Y:总运输时间
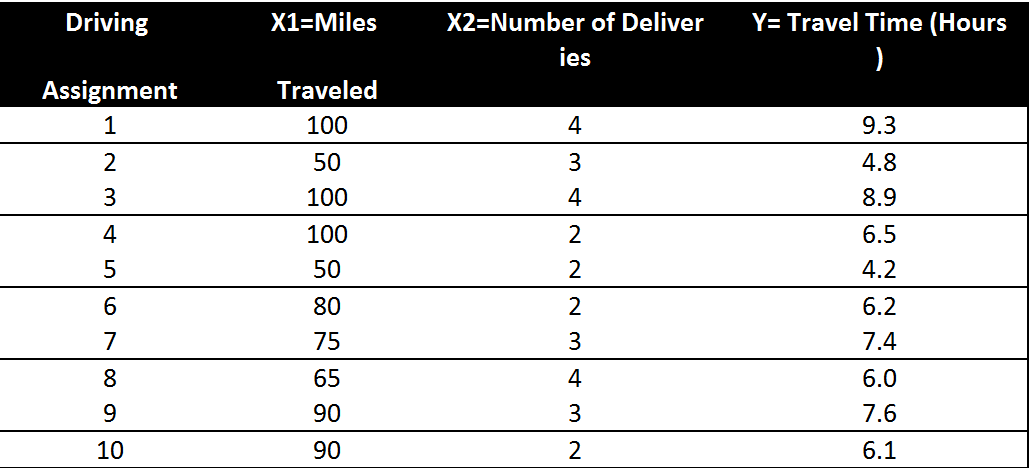
如果一个运输任务是跑102英里,运输6次,预计多少小时?
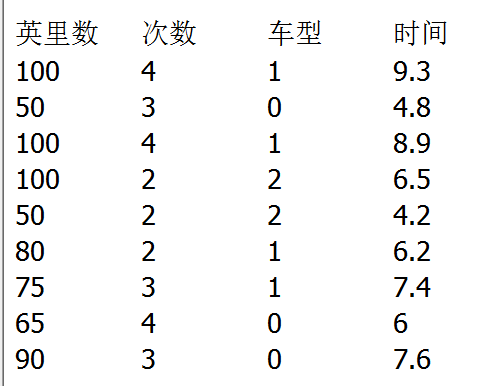
8. 如果自变量中有分类型变量(categorical data) , 如何处理?
改成 001 010 100 这种形式
9. 关于误差的分布
误差ε是一个随机变量,均值为0
ε的方差对于所有的自变量来说相等
所有ε的值是独立的
ε满足正态分布,并且通过β0+β1x1+β2x2+ ... +βpxp反映y的期望值
四、代码部分
解答7:
from numpy import genfromtxt
from sklearn import linear_model # 可以直接调用回归分析
dataPath = r"Delivery.csv"
deliveryData = genfromtxt(dataPath, delimiter=',') # 转化数据格式
print("data")
print(deliveryData)
x = deliveryData[:, :-1] # -1代表最后一列,这里取到倒数第二列
y = deliveryData[:, -1] # 所有行,和最后一列
print(x)
print(y)
lr = linear_model.LinearRegression() # 线性回归
lr.fit(x, y)
print(lr)
print("coefficients:") # b1 b2
print(lr.coef_)
print("intercept:") # b0
print(lr.intercept_)
xPredict = [102, 6].reshape(1, -1)
yPredict = lr.predict(xPredict)
print("predict:")
print (yPredict)
# predictedY = lr.predict(xPredict)
#
# print("predictedY: " + str(predictedY))
加上车型:转化为001
from numpy import genfromtxt
from sklearn import linear_model
# dataPath=r"Delivery_Dummy.csv"
# data = genfromtxt(datapath,delimiter=",")
dataPath = r"Delivery_Dummy.csv"
deliveryData = genfromtxt(dataPath, delimiter=',') # 转化数据格式
print("data")
print(deliveryData)
x = deliveryData[1:,:-1]
y = deliveryData[1:,-1]
print (x)
print (y)
mlr = linear_model.LinearRegression()
mlr.fit(x, y)
print (mlr)
print ("coef:")
print (mlr.coef_)
print ("intercept")
print (mlr.intercept_)
xPredict = [90,2,0,0,1].reshape(1, -1)
yPredict = mlr.predict(xPredict)
print ("predict:")
print (yPredict)


