图论 竞赛图(tournament)学习笔记
竞赛图(tournament)学习笔记
现在只是知道几个简单的性质。。。
竞赛图也叫有向完全图。
其实就是无向完全图的边有了方向。
有一个很有趣的性质就是:一个tournament要么没有环,如果有环,那么必然有一个三元环。当然,tournament一定没有自环和二元环。
证明的话,开始吧,,
首先我们假定当前的tournament存在一个N元环,那么我们设A,B,C为这个N元环上连续的三个点,那么就会存在AB和BC两条边,又因为是竞赛图,所以一定会存在AC或者CA两者中的一条边。
又可以开始开心地分情况讨论了:
(一),存在CA边,那么很开心,我们已经找到了三元环ABC。
(二),存在AC边,那么我们就会发现B这个点是没有用的了,比如这样:
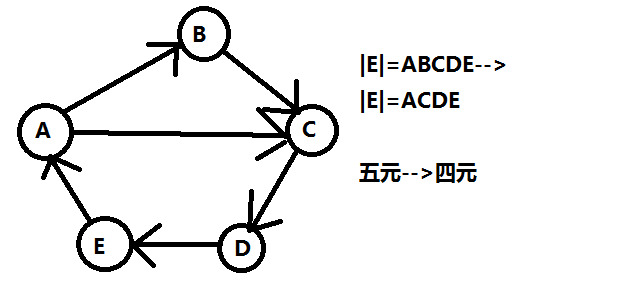
那么我们就可以把一个N元环变成N-1元环了。
那么就一定会缩小到3元环了。
上述性质例题:
CF117C Cycle
一个tournament是一个没有自环的有向图,同时,每两个点之间有一条边连接。这就是说,对于两个点u,v(u≠v),有一条从u到v的边或一条从v到u的边。
给你一个tournament,请找出一个长度为3的环。
直接按照上述性质模拟就好了。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int wx=5017;
inline int read(){
int sum=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
return sum*f;
}
char s[wx][wx];
int vis[wx];
int n;
bool dfs(int u,int fa){
vis[u]=1;
for(int i=1;i<=n;i++){
if(s[u][i]-'0'){
if(s[i][fa]-'0'){
printf("%d %d %d\n",fa,u,i);
return true;
}
if(!vis[i])if(dfs(i,u))return true;
}
}
return false;
}
int main(){
n=read();
for(int i=1;i<=n;i++)
scanf("%s",s[i]+1);
int fl=0;
for(int i=1;i<=n;i++)
if(!vis[i])
if(dfs(i,i))return 0;;
puts("-1");
return 0;
}
关于其他性质:
1:任意竞赛图都有哈密顿路径(经过每个点一次的路径,不要求回到出发点)。
2:竞赛图存在哈密顿回路的充要条件是强联通。
先留坑。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号