一道组合数问题--出自 曹钦翔_wc2012组合计数与动态规划
一道组合数问题--出自 曹钦翔_wc2012组合计数与动态规划
【问题描述】
众所周知,xyc 是一个宇宙大犇,他最近在给他的学弟学妹们出模拟赛。
由于 xyc 实在是太巨了,他出了一套自认为很水的毒瘤模拟赛(看看这题的文件名你就
知道是什么难度了)。
这些题目对于选手来说实在是太 hard 了,愤怒的选手们在评测的时候蜂拥而上,把 xyc
抬了起来……在这一过程中,xyc 用于评测的电脑也被选手们给砸坏了。
尽管选手们的成绩极其惨淡,xyc 还是想研究一下选手们的分数分布情况,他尝试还原
出了电脑中的部分信息:
已知有 n 人参加这场模拟赛,共有 m 道题。现在模拟赛己经结束,评测正在进行中,
对于已经结束评测的试题,已知每名选手这道题的答案是否正确,对于未结束评测的试题,
只知道每名选手是否提交了代码。每个题分数固定,提交正解的选手可以得到这一题的分数
(由于比赛太毒瘤了,每一题没有任何部分分),分数越高排名越靠前,分数相同编号小的
选手排名靠前。
xyc 想知道如果要在排名最靠前的 s 人中选出 t 人,有多少种组合的可能。
xyc 认为这个问题太 naive 了,所以他就把这个问题丢给你了。
【输入格式】
输入文件第一行是 m,接下去 m 行每行一个整数来表示每道题目的分值(整数是正的
表示该题已经评测,否则表示该题尚未评测,该题目的分值为这个整数的绝对值)然后是一个整数 n,接下去是一个 n 行 m 列的字母阵,字母阵只包含 YN 两种字母(Yes
or No)。如果第 i 题已经完成评测,那么这个字母矩阵中第 j 行第 i 列的字母表示第 j 名选
手的第 i 题是否已经得分;如果第 i 题尚未完成评测,那么这个字母矩阵中第 j 行第 i 列的
字母表示第 j 名选手的第 i 题是否提交了代码。
最后两行两个数字,分别为 s 和 t。
如果先选出s个再选出其中t个,可以写爆搜,需要判重比较难写。
不如直接枚举我们选哪t个。
那么就需要分析一波了。
我们需要维护每位选手可以得到分数的最大值和最小值。
这样就可以得出他们分数的大小关系。
先把选手按照第一关键字为最大分数第二关键字为编号的方式排序。
那么就可以得到一些东西,比如说:
对于一个选手i,我们设他是t名里的最后一名,那么他的前面一共有i-1个人,这i-1个人中有t-1个在t名中(这是非常显然的)。
那么我们对于每一个i,就可以去枚举他前面这i-1个人中哪t-1个人在t名中就可以了。
怎么枚举,还有一个需要注意的地方。
就是可能在1到i-1中可能有一些人满足:如果i在前t名,那么这些人必然在前t名。
为什么?其实非常简单:因为这些人的最小分数可能大于i的最大分数。
那么我们就需要计算出究竟有多少个这样的人,这也是我们按照最大分数排序的原因,这样我们就可以将这些人弄在一起。
具体如下图: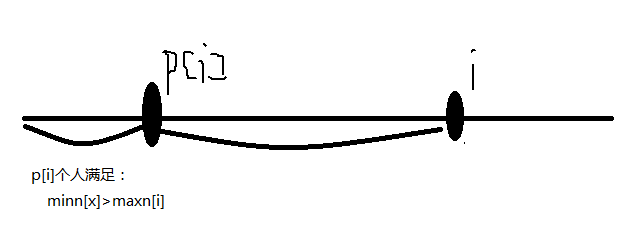
那么我们就成功地把1到i这一段线段分成了两段。
这样之后我们就可以毫无顾虑的开始做数学了。
我们要从这两段中一共选择t个人(第i个人必选)
那么枚举一个量j设为在第一段中也就是前p[i]个人中有j个人被选中,那么就会有t-j-1个人在第二段也就是后\(i-1-p[i]\)被选中。
直接组合数?
并不,因为j还要有一些范围。
1,\(j<=p[i]\)显然吧
2,\(j<=t-1\)第i个人必选
3,\(j>=p[i]+t-s\),因为\(p[i]-j\)是第一段中不被选的,\(s-t\)是总共不会选的,那么就有:\(p[i]-j<=s-t\)
4,\(p[i]+1<=s\)这样i才会在前s名中。
这样确定了j的范围之后,枚举j就可以了。
即
另外,求组合数不能用阶乘,用O(N)递推。
即
既然都会了,那就可以愉快地打代码了。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int wx=117;
inline int read(){
int sum=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
return sum*f;
}
struct node{
int pts1,pts2; int flag,id;
friend bool operator < (const node & a,const node & b){
if(a.pts1==b.pts1)return a.id<b.id;
return a.pts1>b.pts1;
}
}a[wx],b[wx];
int n,m,T,S,ans;
int vis[wx],flag[wx],t[wx],tt[wx],p[wx];
char c[wx];
int Abs(int x){
if(x<0)return -x;
return x;
}
int C(int nn,int mm){
if(nn<0||mm<0)return 0;
if(mm==0)return 1;
if(nn==0)return 0;
if(nn==mm)return 1;
if(mm>nn)return 0;
int re=1;
for(int i=0;i<nn-mm;i++){
re=re*(nn-i)/(i+1);
}
return re;
}
signed main(){
freopen("ctsc.in","r",stdin);
freopen("ctsc.out","w",stdout);
n=read();
for(int i=1;i<=n;i++){
int x=read();
if(x>0)flag[i]=1;
t[i]=Abs(x);
}
m=read();
for(int i=1;i<=m;i++){
scanf("%s",c+1);
a[i].id=i;
for(int j=1;j<=n;j++){
if(flag[j])
{
if(c[j]=='Y')a[i].pts1+=t[j],a[i].pts2+=t[j];
}
else
{
if(c[j]=='Y')a[i].pts1+=t[j];
}
}
}
S=read(); T=read();
sort(a+1,a+1+m);
for(int i=1;i<=m;i++){
for(int j=1;j<i;j++){
p[i]+=((a[j].pts2>a[i].pts1)||(a[j].pts2==a[i].pts1&&a[j].id<a[i].id));
}
}
for(int i=T;i<=m;i++){
if(p[i]>S)break;
int don=max(p[i]-S+T,(long long)0);
int upp=min(p[i],T-1);
for(int j=don;j<=upp;j++){
ans+=C(p[i],j)*C(i-p[i]-1,T-j-1);
}
}
printf("%lld\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号