缩点【洛谷P1262】 间谍网络

【洛谷P1262】 间谍网络

题目描述

由于外国间谍的大量渗入，国家安全正处于高度的危机之中。如果A间谍手中掌握着关于B间谍的犯罪证据，则称A可以揭发B。有些间谍收受贿赂，只要给他们一定数量的美元，他们就愿意交出手中掌握的全部情报。所以，如果我们能够收买一些间谍的话，我们就可能控制间谍网中的每一分子。因为一旦我们逮捕了一个间谍，他手中掌握的情报都将归我们所有，这样就有可能逮捕新的间谍，掌握新的情报。

我们的反间谍机关提供了一份资料，包括所有已知的受贿的间谍，以及他们愿意收受的具体数额。同时我们还知道哪些间谍手中具体掌握了哪些间谍的资料。假设总共有n个间谍(n不超过3000)，每个间谍分别用1到3000的整数来标识。

请根据这份资料，判断我们是否有可能控制全部的间谍，如果可以，求出我们所需要支付的最少资金。否则，输出不能被控制的一个间谍。

一个环内的点当做一个点，进行有向图缩点，缩点之后的点权就是该点包括的点的点权最小值。

之后重新建图，对于每个点如果他的点权不是无限大，那么就可以从他开始扩展，dfn就可以解决。不过有一点问题，就是如果可以遍历所有点，那么我们是需要输出最小代价的。

那么尝试hack一下现在的做法。

可以发现，确实会有地方多计算了点权。

比如下面这个图。

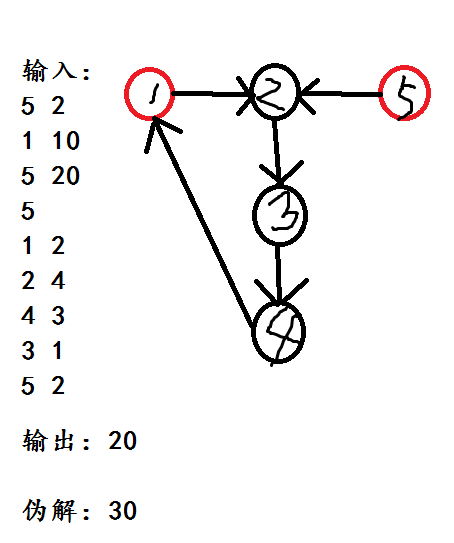
按照当前做法，1号点的点权10也会被计算到答案里，但是我们只需要5号点的点权20就可以了。

所以就有了一个优化，就是统计重新建图之后每个点的入度，然后从入度为零的点开始遍历。

之后再去从入度不为零的点遍历。

code：

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int wx=50017;

inline int read(){
	int sum=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
	while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
	return sum*f;
}

int tot,st[wx],top,col,n,p,m;
int head[wx],h[wx],num,Num;
int dfn[wx],low[wx],belong[wx],size[wx],a[wx],v[wx],vis[wx];
int in[wx];

struct e{
	int nxt,to;
}edge[wx*2];

void add(int from,int to){
	edge[++num].nxt=head[from];
	edge[num].to=to;
	head[from]=num;
}

void Tarjan(int u){
	dfn[u]=low[u]=++tot;
	st[++top]=u;
	for(int i=head[u];i;i=edge[i].nxt){
		int v=edge[i].to;
		if(!dfn[v]){
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(!belong[v]){
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(low[u]==dfn[u]){
		belong[u]=++col;
		size[col]++;
		while(st[top]!=u){
			belong[st[top]]=col;
			size[col]++;
			top--;
		}
		top--;
	}
}

struct node{
	int nxt,to;
}e[wx*2];

void Add(int from,int to){
	e[++Num].nxt=h[from];
	e[Num].to=to;
	h[from]=Num;
}

void dfs(int u){
	vis[u]=1;
	for(int i=h[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(vis[v])continue;
		dfs(v);
	}
}

int main(){
	n=read(); p=read();
	memset(a,0x3f,sizeof a);
	memset(v,0x3f,sizeof v);
	for(int i=1;i<=p;i++){
		int x; x=read(); a[x]=read();
	}
	m=read();
	for(int i=1;i<=m;i++){
		int x,y;
		x=read(); y=read();
		add(x,y);
	}
	for(int i=1;i<=n;i++)if(!dfn[i])Tarjan(i);
	for(int i=1;i<=n;i++)v[belong[i]]=min(v[belong[i]],a[i]);
	for(int u=1;u<=n;u++){
		for(int i=head[u];i;i=edge[i].nxt){
			int v=edge[i].to;
			if(belong[v]!=belong[u])in[belong[v]]++,Add(belong[u],belong[v]);
		}
	}
	int ans=0;
	
	for(int i=1;i<=col;i++){
		if(v[i]!=0x3f3f3f3f&&vis[i]==0&&in[i]==0){
			if(i==1)
			vis[i]=1;ans+=v[i];dfs(i);
		}
	}
	
	for(int i=1;i<=col;i++){
		if(v[i]!=0x3f3f3f3f&&vis[i]==0){
			if(i==1)
			vis[i]=1;ans+=v[i];dfs(i);
		}
	}
	
	for(int i=1;i<=n;i++){
		if(!vis[belong[i]]){
			puts("NO");
			printf("%d\n",i); return 0;
		}
	}
	puts("YES");
	printf("%d\n",ans);
	return 0;
}