论文笔记之：Semi-supervised Classification with Graph Convolutional Networks

 

Semi-supervised Classification with Graph Convolutional Networks

2018-01-16  22:33:36 

 

1. 文章主要思想：

2. 代码实现（Pytorch）：https://github.com/tkipf/pygcn  

 

【Introduction】：

本文尝试用 GCN 进行半监督的分类，通过引入一个 graph Laplacian regularization term 到损失函数中：

其中，L0 代表损失函数，即：graph 的标注部分，f(*) 可以是类似神经网络的可微分函数，X 是节点特征向量组成的矩阵， 代表 无向图 g 的 unnormalized graph Laplacian，及其邻接矩阵 A，degree matrix $D_{ii} = \sum_{j} A_{ij}$. 公式（1）是依赖于假设：connected nodes in the graph are likely to share the same label. 但是这个假设，可能限制了模型的适应性（the modeling capacity），因为 graph edges 不需要编码 node 的相似性，但可以包含额外的信息。

 

在这个工作中，我们直接用神经网络模型 f(X, A) 来编码 graph 结构，然后在有label 的节点上进行训练，所以，避免了显示的 在损失函数中，基于 graph 的正则化项。基于 f(*) 在 graph 上的近邻矩阵将会允许模型从监督loss L0 来分布梯度信息，也确保其可以学习 nodes 的表示。

 

本文的创新点主要由两个部分：

1. we introduce a localized and well-behaved propagation rule for graph convolutional neural networks, and show it can be motived from a first-order approximation of spectral convolutions on graphs.

2. we show how this form of a graph convolutional neural network can be used for fast and scalable semi-supervised classification of nodes in a graph.

 

【Fast Approximate Convolutions on Graphs】:

我们利用下面的传递规则 来构建多层 Graph Convolutional Network（GCN）：

其中，是无向图 g 的邻接矩阵 加上 自我连接。$I_N$ 是单位矩阵，和 $W^l$ 是 特定层的可训练权重矩阵。$\delta(*)$ 代表激活函数，例如 ReLU(*)。$H^l$ 是第 l 层的激活的矩阵。

 

接下来，我们表明这种形式的传递规则可以由 first-order approximation of localized spectral filters on graphs 启发而来。我们将 graph 上的 spectral convolutions 定义为 一个信号 x 和 filter $g_{\theta} = diag(\theta)$ 在傅里叶领域的乘积，参数化为 $\theta$，即：

  其中，U 是归一化的 graph Laplacian 的特征向量的矩阵（the matrix of eigenvectors of the normalized graph Laplacian），，with a diagonal matrix of its eigenvalues ^ and $U^T x$ being the graph Fourier transform of x. 我们可以将 $g_{\theta}$ 看做是 L的奇异值的函数，即：。评估上述公式，计算量比较大，因为奇异值矩阵乘积的复杂度是 $O(N^2)$。此外，计算 L 的特征值分解可能对于大型的 graph 来说代价也比较昂贵。为了解决这个问题，Hammond et al. 在 2011年提出，可以用一个 truncated expansion 来很好的估计：

其中， 。$\lambda_{max}$ 代表 L 的最大奇异值。$\theta'$ 现在是 Chebyshev coefficients 的向量。这里引出了一个新的概念【Chebyshev polynomials】，其定义为：$T_k(x) = 2xT_{k-1}(x) - T_{k-2}(x)$ with $T_0(x) = 1$ and $T_1(x) = x$。读者可以继续研究下这两篇 paper，来更好的理解这个近似：【1】【2】。

【1】Hammond, David K, Vandergheynst, Pierre, and Gribonval, Remi. Wavelets on graphs via spectral graph theory. Applied and Computational Harmonic Analysis, 30(2):129–150, 2011

【2】Defferrard, Michael, Bresson, Xavier, and Vandergheynst, Pierre. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in Neural Information Processing Systems, 2016

重新回到我们关于 a signal x and a filter $g_{\theta'}$ 的定义，我们现在有：

 其中，；可以很简单的验证：。注意到这个表达式具有下面的性质：。注意到，this experssion is now K-localized sinece it is a K-th localized since it is a K-th order polynomial in the Laplacian, i.e. it depends only on nodes that are at maximum K steps away from the central node (K-th order neighborhood)。评估上述公式的复杂度为 $O(E)$，即：与边的个数有关。Defferrard et al. 【2】利用这个 K-localized convolution 来定义 graphs 上的卷积神经网络。

 

在这个工作中，我们建议 keeping only terms up to order k=1 来估计上述公式。原因如下：as we intend to stack multiple layers of parameterized graph convolutions followed by non-linearities, we expect that a per-layer convolution operation that is linear with respect to the adjacency matrix increases modeling capacity while keeping the comptational complexity comparable to a single graph convolution with k > 1. We further approximate $\lambda_{max} 约等于 2$，as we can expect that neural network parameters will adapt to this change in scale during training.

有了这些近似，我们有：

有两个 free parameters $\theta_0^'$ and $\theta_1^'$. 公式（6）可以理解为 利用一个参数化的 filter 仅仅在一个节点的直接近邻上进行局部卷积操作。这些 filter 的参数可以在整个 graph 上进行参数共享。随后的这种 filters 可以有效的卷积一个节点的 k-th order 的近邻，其中 k is the number of successive filtering operations or convolutional layers in the neural network model. 

 

实际上，进一步的限制参数的数量，可以降低每一层的许多操作（如 matrix multiplication）。我们可以写作：

这里就仅仅有一个参数了 $\theta = \theta_0^' = -\theta_1^'$。注意到，现在奇异值的范围[0, 2]。重复的利用这个操作符，可能会引起不稳定或者梯度消失、爆炸等情况，当在一个深度神经网络模型中进行应用的时候。为了消除这种问题，我们引入如下的 renormalization trick：

 

 

我们将这种形式拓展到 signal X with C input channels （i.e. a C-dimensional feature vector for every node）and F filters or feature maps as follows:

其中， 现在是 filter 参数的矩阵，Y 是卷积的信号矩阵。这个 filter operation 的复杂度是 $O(|E|FC)$，因为 可以有效的执行，as a product of a sparse matrix with a dense matrix.

 

【Semi-supervised Node Classification 】

　　有了上述灵活的模型 f(X, A) 在 graph 上进行有效的信息传递，我们可以重新回到半监督节点分类的问题。像 introduction 中列出来的那样，我们可以 relax 在基于 graph 的半监督学习中的常规假设，通过 conditioning our model f(X, A) both on the data X and on the adjacency matrix A of the underlying graph structure. 我们希望这种设定可以在特定的场景下特别有效：the adjacency matrix contains information not present in the data X. 总体的模型，例如：一个多层的 GCN 进行半监督学习，如图1所示的那样。

　　3.1 Example : 

　　我们考虑一个两层的 GCN 进行半监督节点分类（a two-layer GCN for semi-supervised node classification on a graph with a symmetric adjacency matrix A (binary or weighted)）。 我们首先在预处理的步骤中计算 。我们的前向传播模型可以采用下面简单的形式：

　　

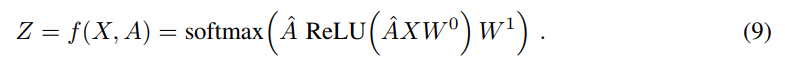
其中，$W^0$ is a input-to-hidden weight matrix for a hidden layer with H feature maps. $W^1$ is a hidden-to-output weight matrix. 对于半监督的多类别分类，我们采用 the  cross-entropy error over all labeled examples: 

　　

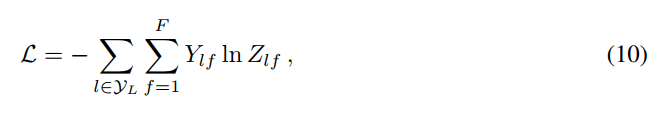
　　其中，$y_L$ 是带有标签的节点集合（the set of node indices that have labels）。

　　神经网络的权重 $W^0$ and $W^1$ 是用 gradient descent 进行训练的。在这个工作中，我们利用全部的数据集，进行批梯度下降，进行每一次的训练迭代。

　　

　　

---

Pytorch 代码实现：

1. train.py : 

数据的加载 

 

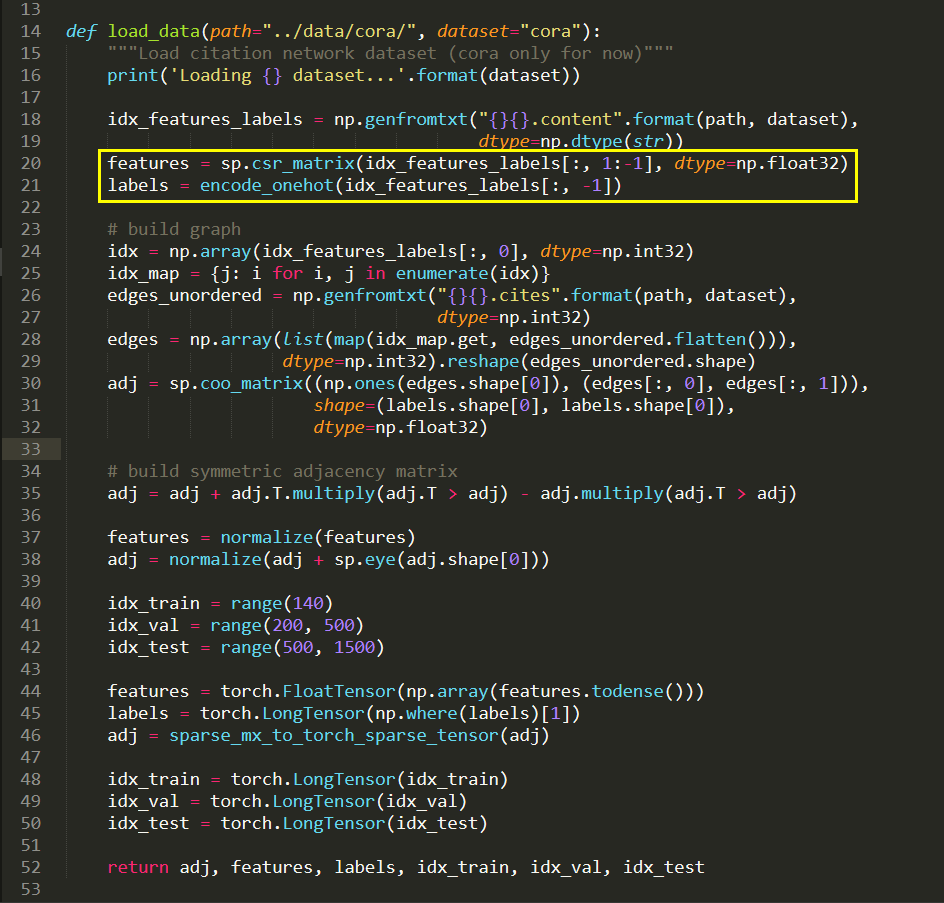
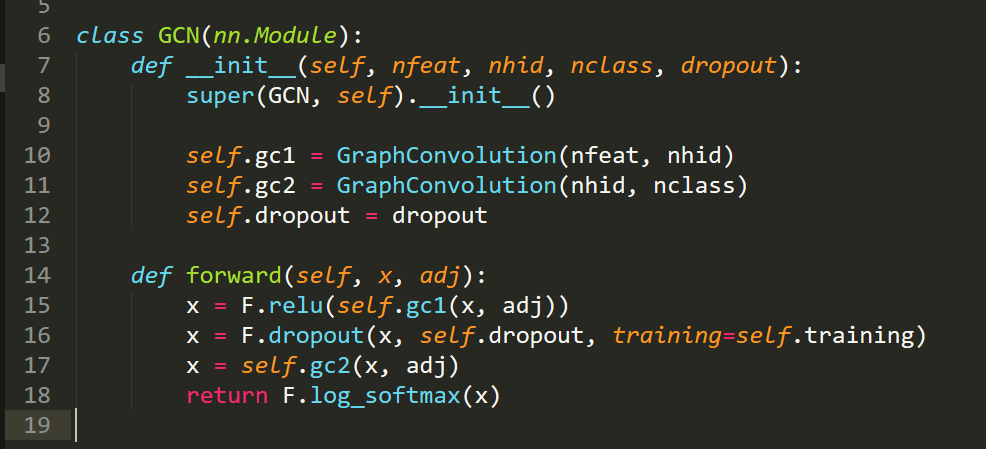
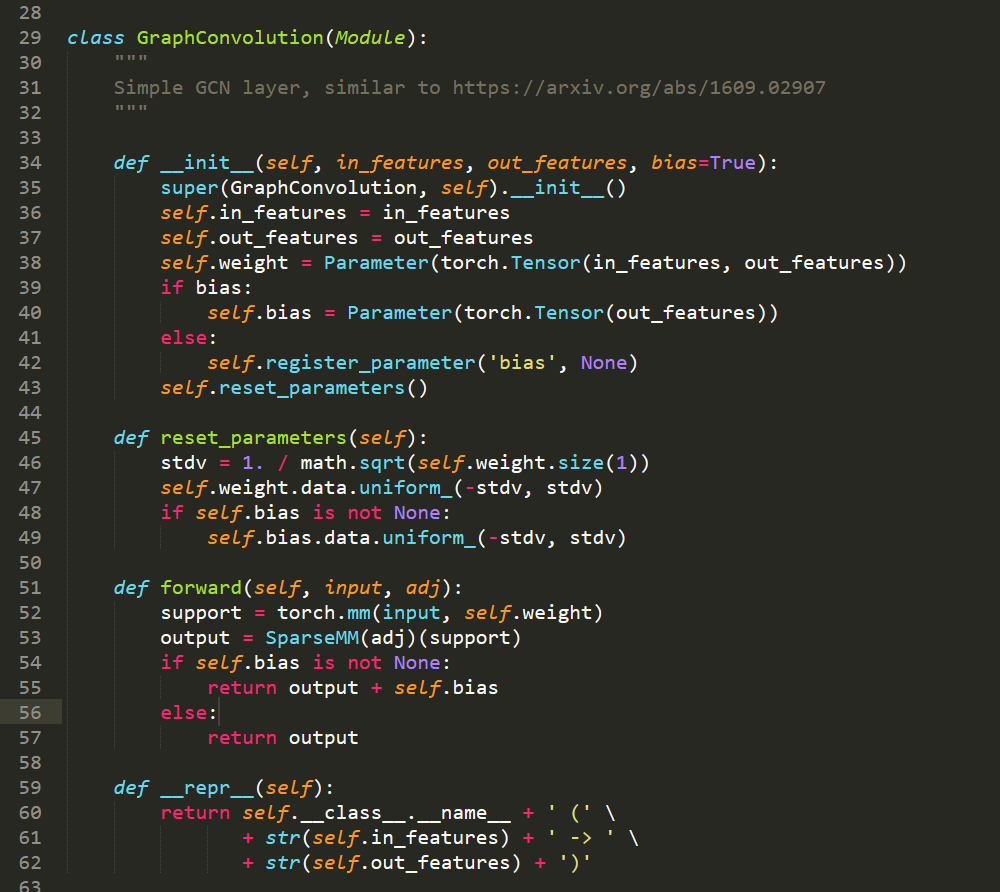
2. Layer 的定义：