一文读懂 深度强化学习算法 A3C (Actor-Critic Algorithm)
一文读懂 深度强化学习算法 A3C (Actor-Critic Algorithm)
2017-12-25 16:29:19
对于 A3C 算法感觉自己总是一知半解,现将其梳理一下,记录在此,也给想学习的小伙伴一个参考。
想要认识清楚这个算法,需要对 DRL 的算法有比较深刻的了解,推荐大家先了解下 Deep Q-learning 和 Policy Gradient 算法。
我们知道,DRL 算法大致可以分为如下这几个类别:Value Based and Policy Based,其经典算法分别为:Q-learning 和 Policy Gradient Method。
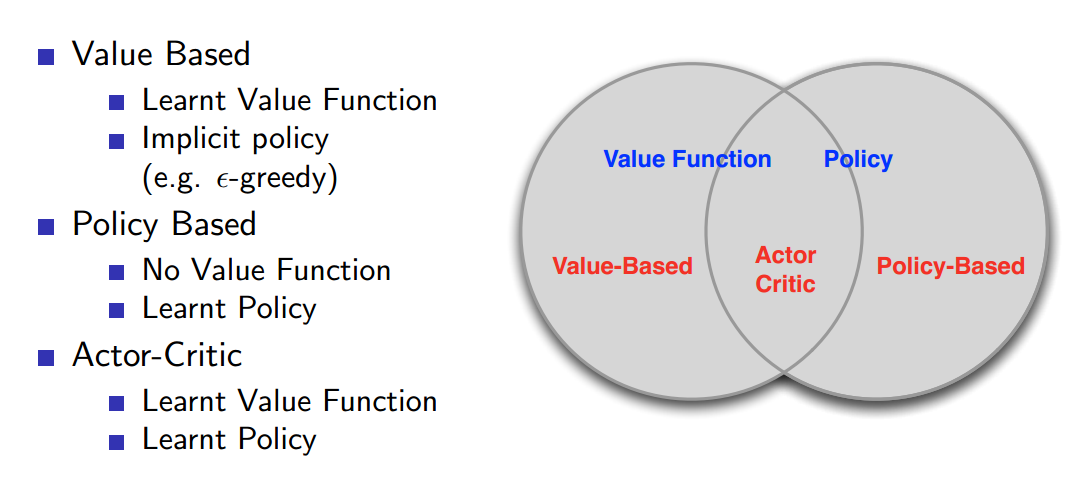
而本文所涉及的 A3C 算法则是结合 Policy 和 Value Function 的产物,其中,基于 Policy 的方法,其优缺点总结如下:
Advantages:
1. Better convergence properties (更好的收敛属性)
2. Effective in high-dimensional or continuous action spaces(在高维度和连续动作空间更加有效)
3. Can learn stochastic policies(可以Stochastic 的策略)
Disadvantages:
1. Typically converge to a local rather than global optimum(通常得到的都是局部最优解)
2. Evaluating a policy is typically inefficient and high variance
(评价策略通常不是非常高效,并且有很高的偏差)
我们首先简要介绍一些背景知识(Background):
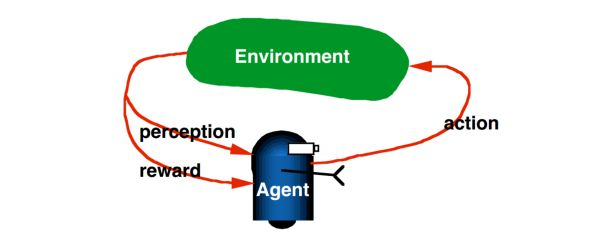
在 RL 的基本设置当中,有 agent,environment, action, state, reward 等基本元素。agent 会与 environment 进行互动,而产生轨迹,通过执行动作 action,使得 environment 发生状态的变化,s -> s' ;然后 environment 会给 agent 当前 动作选择以 reward(positive or negative)。通过不断的进行这种交互,使得积累越来越多的 experience,然后更新 policy,构成这个封闭的循环。为了简单起见,我们仅仅考虑 deterministic environment,即:在状态 s 下,选择 action a 总是会得到相同的 状态 s‘。
为了清楚起见,我们先定义一些符号:
1. stochastic policy $\pi(s)$ 决定了 agent's action, 这意味着,其输出并非 single action,而是 distribution of probability over actions (动作的概率分布),sum 起来为 1.
2. $\pi(a|s)$ 表示在状态 s 下,选择 action a 的概率;
而我们所要学习的策略 $\pi$,就是关于 state s 的函数,返回所有 actions 的概率。
我们知道,agent 的目标是最大化所能得到的奖励(reward),我们用 reward 的期望来表达这个。在概率分布 P 当中,value X 的期望是:
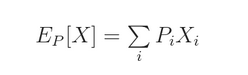
其中 Xi 是 X 的所有可能的取值,Pi 是对应每一个 value 出现的概率。期望就可以看作是 value Xi 与 权重 Pi 的加权平均。
这里有一个很重要的事情是: if we had a pool of values X, ratio of which was given by P, and we randomly picked a number of these, we would expect the mean of them to be . And the mean would get closer to
as the number of samples rise.
我们再来定义 policy $\pi$ 的 value function V(s),将其看作是 期望的折扣回报 (expected discounted return),可以看作是下面的迭代的定义:
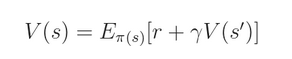
这个函数的意思是说:当前状态 s 所能获得的 return,是下一个状态 s‘ 所能获得 return 和 在状态转移过程中所得到 reward r 的加和。
此外,还有 action value function Q(s, a),这个和 value function 是息息相关的,即:
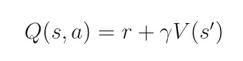
此时,我们可以定义一个新的 function A(s, a) ,这个函数称为 优势函数(advantage function):
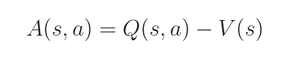
其表达了在状态 s 下,选择动作 a 有多好。如果 action a 比 average 要好,那么,advantage function 就是 positive 的,否则,就是 negative 的。
Policy Gradient:
当我们构建 DQN agent 的时候,我们利用 NN 来估计的是 Q(s, a) 函数。这里,我们采用不同的方法来做,既然 policy $\pi$ 是 state $s$ 的函数,那么,我们可以直接根据 state 的输入 来估计策略的选择嘛。
这里,我们 NN 的输入是 state s,输出是 an action probability distribution $\pi_\theta$,其示意图为:
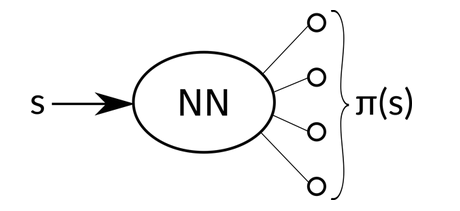
实际的执行过程中,我们可以按照这个 distribution 来选择动作,或者 直接选择 概率最大的那个 action。
但是,为了得到更好的 policy,我们必须进行更新。那么,如何来优化这个问题呢?我们需要某些度量(metric)来衡量 policy 的好坏。
我们定一个函数 $J(\pi)$,表示 一个策略所能得到的折扣的奖赏,从初始状态 s0 出发得到的所有的平均:
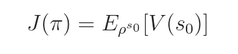
我们发现这个函数的确很好的表达了,一个 policy 有多好。但是问题是很难估计,好消息是:we don't have to。
我们需要关注的仅仅是如何改善其质量就行了。如果我们知道这个 function 的 gradient,就变的很 trivial (专门查了词典,这个是:琐碎的,微不足道的,的意思,恩,不用谢)。
有一个很简便的方法来计算这个函数的梯度:
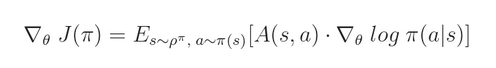
这里其实从 目标函数 到这个梯度的变换,有点突然,我们先跳过这个过程,就假设已经是这样子了。后面,我再给出比较详细的推导过程。
这里可以参考 Policy Gradient 的原始paper:Policy Gradient Methods for Reinforcement Learning with Function Approximation
或者是 David Silver 的 YouTube 课程:https://www.youtube.com/watch?v=KHZVXao4qXs
简单而言,这个期望内部的两项:
第一项,是优势函数,即:选择该 action 的优势,当低于 average value 的时候,该项为 negative,当比 average 要好的时候,该项为 positive;是一个标量(scalar);
第二项,告诉我们了使得 log 函数 增加的方向;
将这两项乘起来,我们发现:likelihood of actions that are better than average is increased, and likelihood of actions worse than average is decreased.
Fortunately, running an episode with a policy π yields samples distributed exactly as we need. States encountered and actions taken are indeed an unbiased sample from the and π(s) distributions. That’s great news. We can simply let our agent run in the environment and record the (s, a, r, s’) samples. When we gather enough of them, we use the formula above to find a good approximation of the gradient
. We can then use any of the existing techniques based on gradient descend to improve our policy.
Actor-Critic:
我们首先要计算的是优势函数 A(s, a),将其展开:
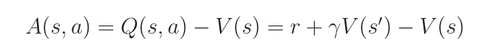
运行一次得到的 sample 可以给我们提供一个 Q(s, a) 函数的 unbiased estimation。我们知道,这个时候,我们仅仅需要知道 V(s) 就可以计算 A(s, a)。
这个 value function 是容易用 NN 来计算的,就像在 DQN 中估计 action-value function 一样。相比较而言,这个更简单,因为 每个 state 仅仅有一个 value。
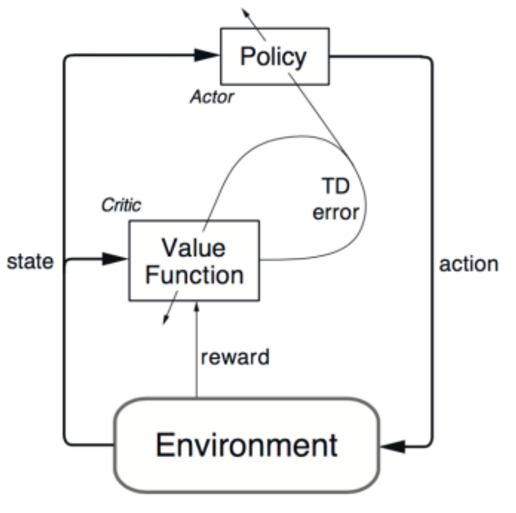
我们可以将 value function 和 action-value function 联合的进行预测。最终的网络框架如下:
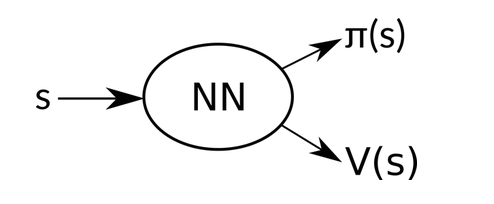
这里,我们有两个东西需要优化,即: actor 以及 critic。
actor:优化这个 policy,使得其表现的越来越好;
critic:尝试估计 value function,使其更加准确;
这些东西来自于 the Policy Gradient Theorem :
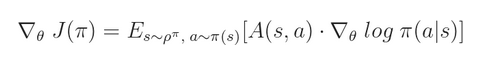
简单来讲,就是:actor 执行动作,然后 critic 进行评价,说这个动作的选择是好是坏。
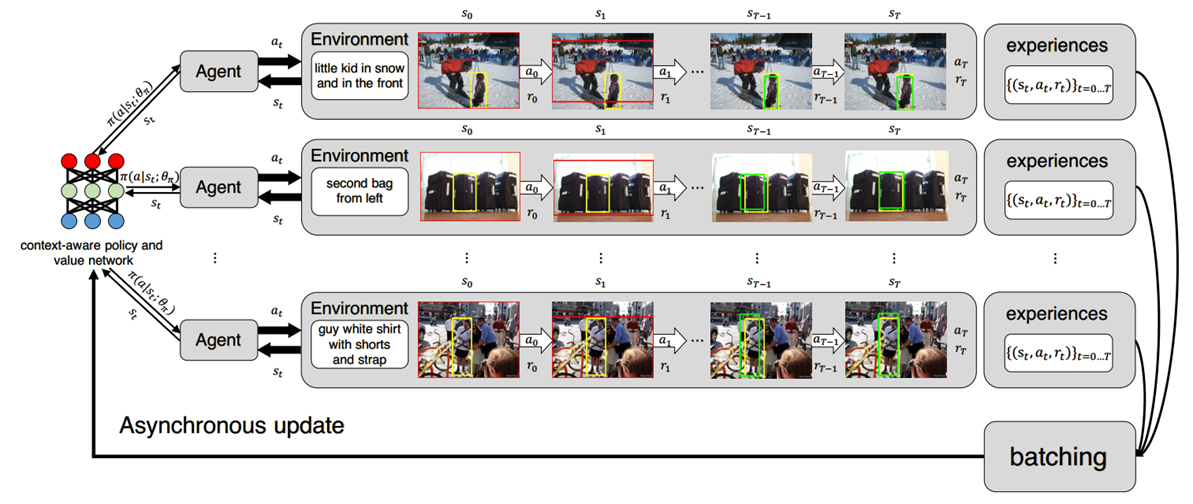
Parallel agents:
如果只用 单个 agent 进行样本的采集,那么我们得到的样本就非常有可能是高度相关的,这会使得 machine learning 的model 出问题。因为 machine learning 学习的条件是:sample 满足独立同分布的性质。但是不能是这样子高度相关的。在 DQN 中,我们引入了 experience replay 来克服这个难题。但是,这样子就是 offline 的了,因为你是先 sampling,然后将其存储起来,然后再 update 你的参数。
那么,问题来了,能否 online 的进行学习呢?并且在这个过程中,仍然打破这种高度相关性呢?
We can run several agents in parallel, each with its own copy of the environment, and use their samples as they arrive.
1. Different agents will likely experience different states and transitions, thus avoiding the correlation2.
2. Another benefit is that this approach needs much less memory, because we don’t need to store the samples.
此外,还有一个概念也是非常重要的:N-step return 。
通常我们计算的 Q(s, a), V(s) or A(s, a) 函数的时候,我们只是计算了 1-step 的 return。
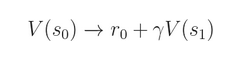
在这种情况下,我们利用的是从 sample (s0, a0, r0, s1)获得的 即刻奖励(immediate return),然后该函数下一步预测 value 给我们提供了一个估计 approximation。但是,我们可以利用更多的步骤来提供另外一个估计:
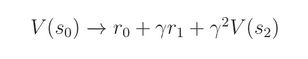
或者 n-step return:
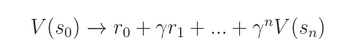
The n-step return has an advantage that changes in the approximated function get propagated much more quickly. Let’s say that the agent experienced a transition with unexpected reward. In 1-step return scenario, the value function would only change slowly one step backwards with each iteration. In n-step return however, the change is propagated n steps backwards each iteration, thus much quicker.
N-step return has its drawbacks. It’s higher variance because the value depends on a chain of actions which can lead into many different states. This might endanger the convergence.
这个就是 异步优势actor-critic 算法(Asynchronous advantage actor-critic , 即:A3C)。

以上是 A3C 的算法部分,下面从 coding 的角度来看待这个算法:
基于 python+Keras+gym 的code 实现,可以参考这个 GitHub 链接:https://github.com/jaara/AI-blog/blob/master/CartPole-A3C.py
所涉及到的大致流程,可以归纳为:
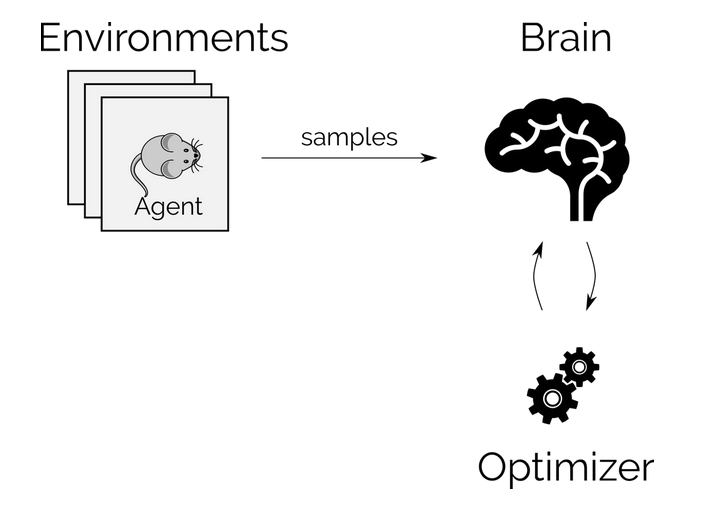
在这其中,最重要的是 loss function 的定义:
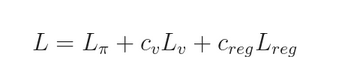
其中, is the loss of the policy,
is the value error and
is a regularization term. These parts are multiplied by constants
and
, which determine what part we stress more.
下面分别对这三个部分进行介绍:
1. Policy Loss:
我们定义 objective function $J(\pi)$ 如下:

这个是:通过策略 $\pi$ 平均所有起始状态所得到的总的 reward(total reward an agent can achieve under policy $\pi$ averaged over all starting states)。
根据 Policy Gradient Theorem 我们可以得到该函数的 gradient:
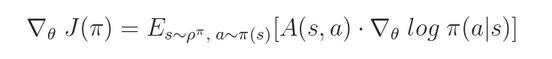
我们尝试最大化这个函数,那么,对应的 loss 就是这个 负函数:
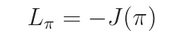
我们将 A(s,a) 看做是一个 constant,然后重新将上述函数改写为如下的形式:
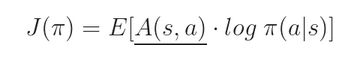
我们就对于minibatch 中所有样本进行平均,来扫一遍这个期望值。最终的 loss 可以记为:
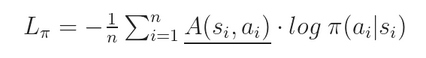
2. Value Loss:
the truth value function V(s) 应该是满足 Bellman Equation 的:
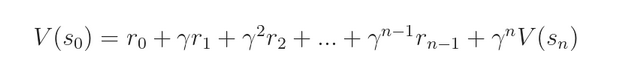
而我们估计的 V(s) 应该是收敛的,那么,根据上述式子,我们可以计算该 error:

这里大家可能比较模糊,刚开始我也是比较晕,这里的 groundtruth 是怎么得到的???
其实这里是根据 sampling 到的样本,然后计算两个 V(s) 之间的误差,看这两个 value function 之间的差距。
所以,我们定义 Lv 为 mean squared error (given all samples):
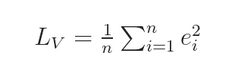
3. Regularizaiton with Policy Entropy :
为何要加这一项呢?我们想要在 agent 与 environment 进行互动的过程中,平衡 探索和利用,我们想去以一定的几率来尝试其他的 action,从而不至于采样得到的样本太过于集中。所以,引入这个 entropy,来使得输出的分布,能够更加的平衡。举个例子:
fully deterministic policy [1, 0, 0, 0] 的 entropy 是 0 ; 而 totally uniform policy[0.25, 0.25, 0.25, 0.25]的 entropy 对于四个value的分布,值是最大的。
我们为了使得输出的分布更加均衡,所以要最大化这个 entropy,那么就是 minimize 这个 负的 entropy。
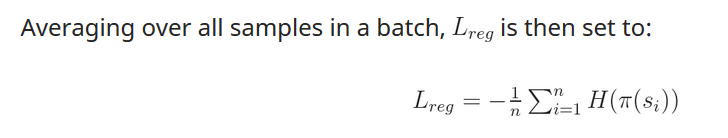
总而言之,我们可以借助于现有的 deep learning 的框架来 minimize 这个这些 total loss,以达到 优化网络参数的目的。
Reference:
1. https://github.com/jaara/AI-blog/blob/master/CartPole-A3C.py
2. https://jaromiru.com/2017/03/26/lets-make-an-a3c-implementation/
3. https://www.youtube.com/watch?v=KHZVXao4qXs
4. https://github.com/ikostrikov/pytorch-a3c
======================================================
Policy Gradient Method 目标函数梯度的计算过程:
======================================================
reference paper:policy-gradient-methods-for-reinforcement-learning-with-function-approximation (NIPS 2000, MIT press)
过去有很多算法都是基于 value-function 进行的,虽然取得了很大的进展,但是这种方法有如下两个局限性:
首先,这类方法的目标在于找到 deterministic policy,但是最优的策略通常都是 stochastic 的,以特定的概率选择不同的 action;
其次,一个任意的小改变,都可能会导致一个 action 是否会被选择。这个不连续的改变,已经被普遍认为是建立收敛精度的关键瓶颈。
而策略梯度的方法,则是从另外一个角度来看待这个问题。我们知道,我们的目标就是想学习一个,从 state 到 action 的一个策略而已,那么,我们有必要非得先学一个 value function 吗?我们可以直接输入一个 state,然后经过 NN,输出action 的distribution 就行了嘛,然后,将 NN 中的参数,看做是可调节的 policy 的参数。我们假设 policy 的实际执行的表现为 $\rho$,即:the averaged reward per step。我们可以直接对这个 $\rho$ 求偏导,然后进行参数更新,就可以进行学习了嘛:
![]()
如果上述公式是成立的,那么,$\theta$ 通常都可以保证可以收敛到局部最优策略。而这个文章就提供了上述梯度的一个无偏估计,这是利用 一个估计的满足特定属性的 value function,从 experience 中进行估计。
1. Policy Gradient Theorem (策略梯度定理)
这里讨论的是标准的 reinforcement learning framework,有一个 agent 与 环境进行交互,并且满足马尔科夫属性。
在每个时刻 $t \in {0, 1, 2, ... }$ 的状态,动作,奖励 分别记为:st, at, rt。而环境的动态特征可以通过 状态转移概率(state transition probability)来刻画。

从上面,可以发现各个概念的符号表示及其意义。
====>> 未完,待续 。。。
======================================================
Pytorch for A3C
======================================================
本文将继续以 Pytorch 框架为基础,从代码层次上来看具体的实现,本文所用的 code,来自于:https://github.com/ikostrikov/pytorch-a3c
代码的层次如下所示:
我们来看几个核心的code:
main.py
====>> 所用到的各种重要的参数设置及其初始化:
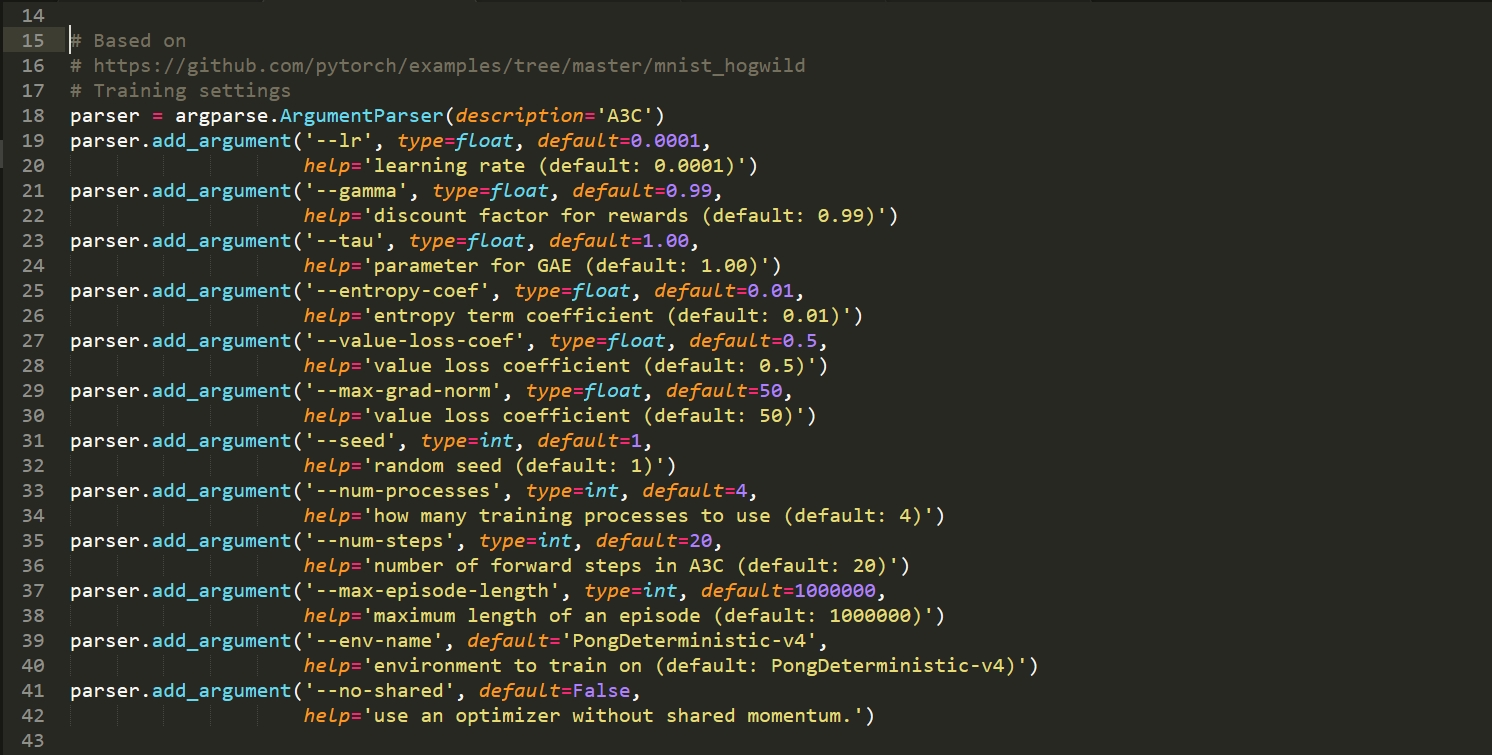
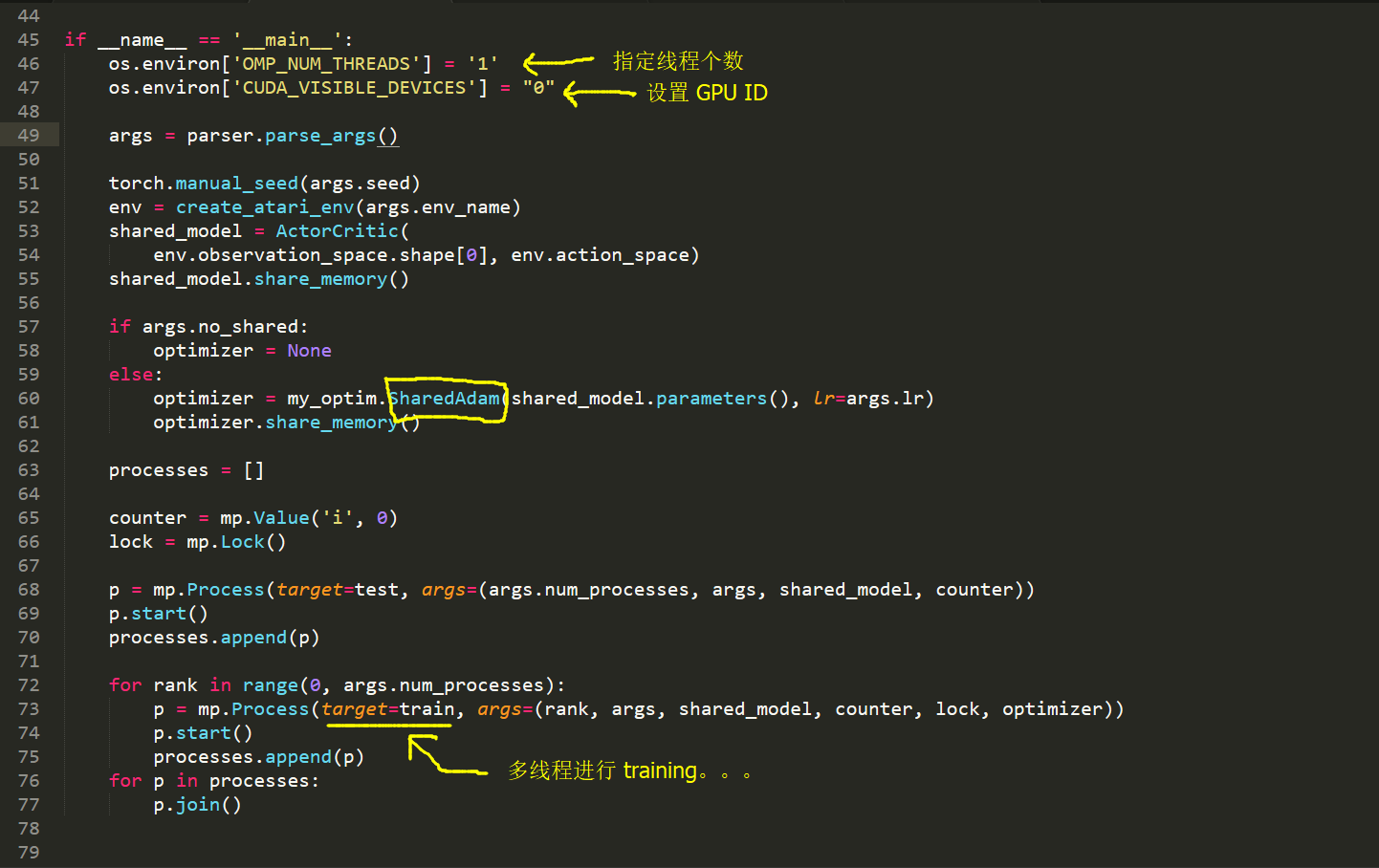
train.py
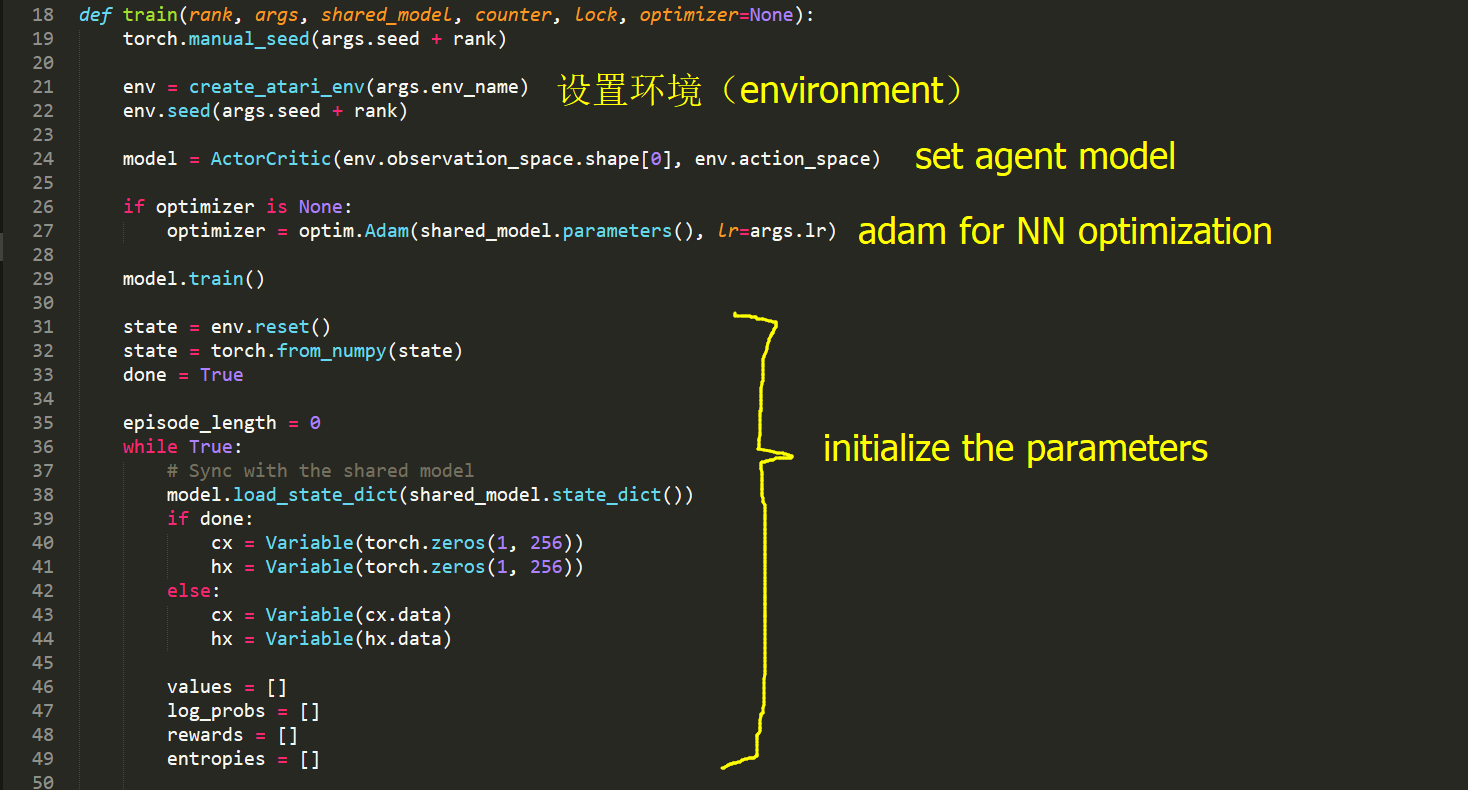
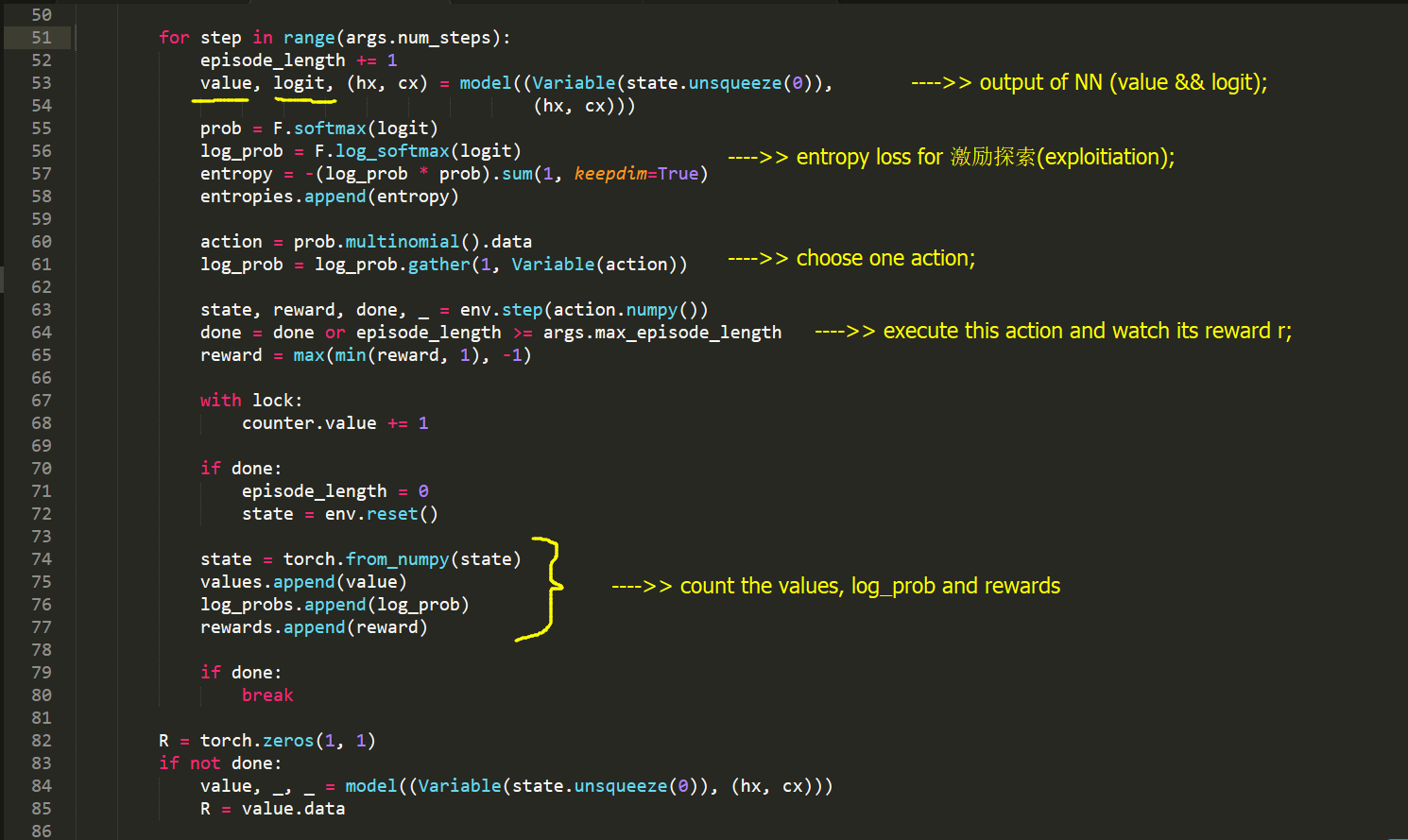
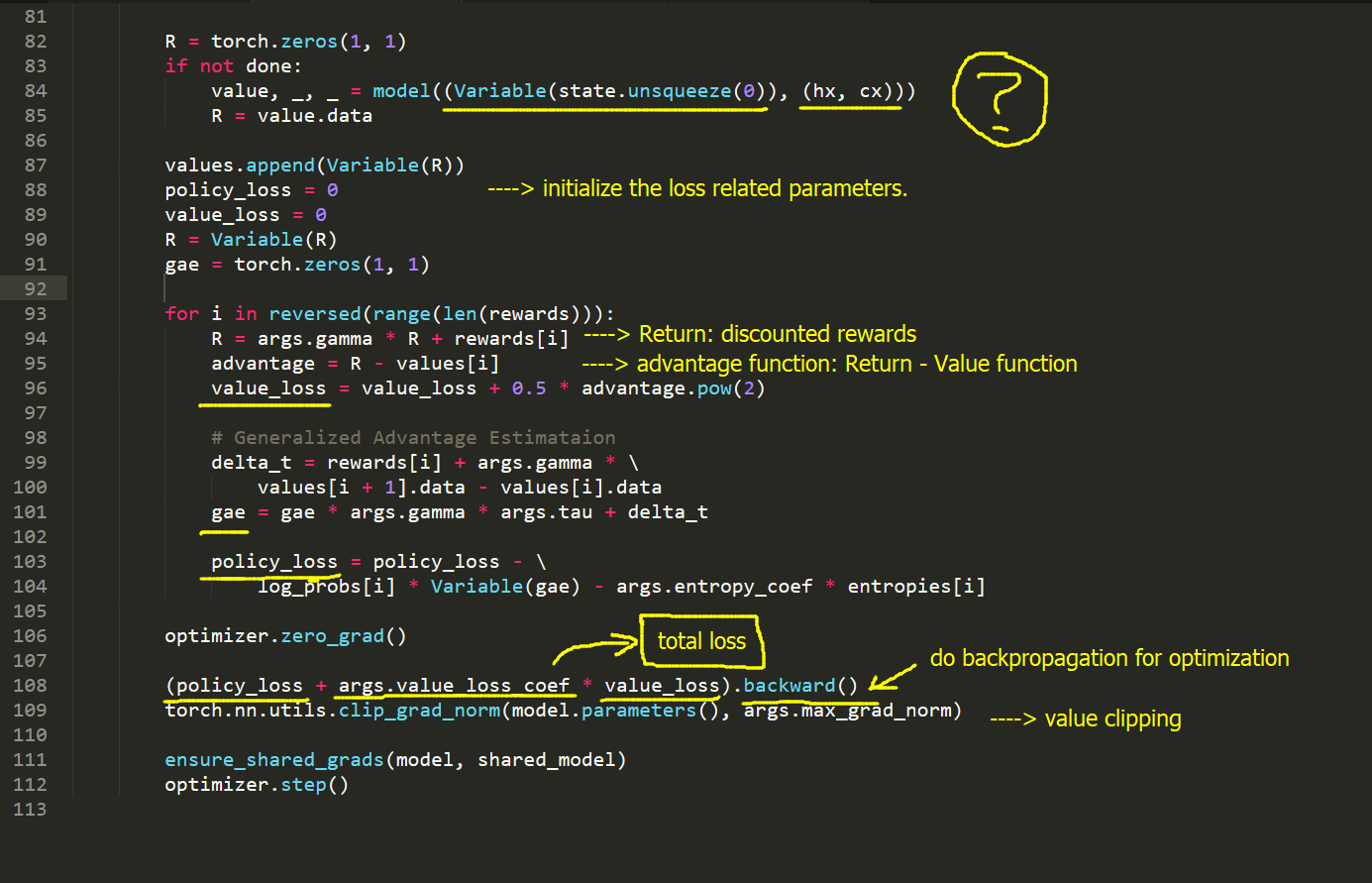
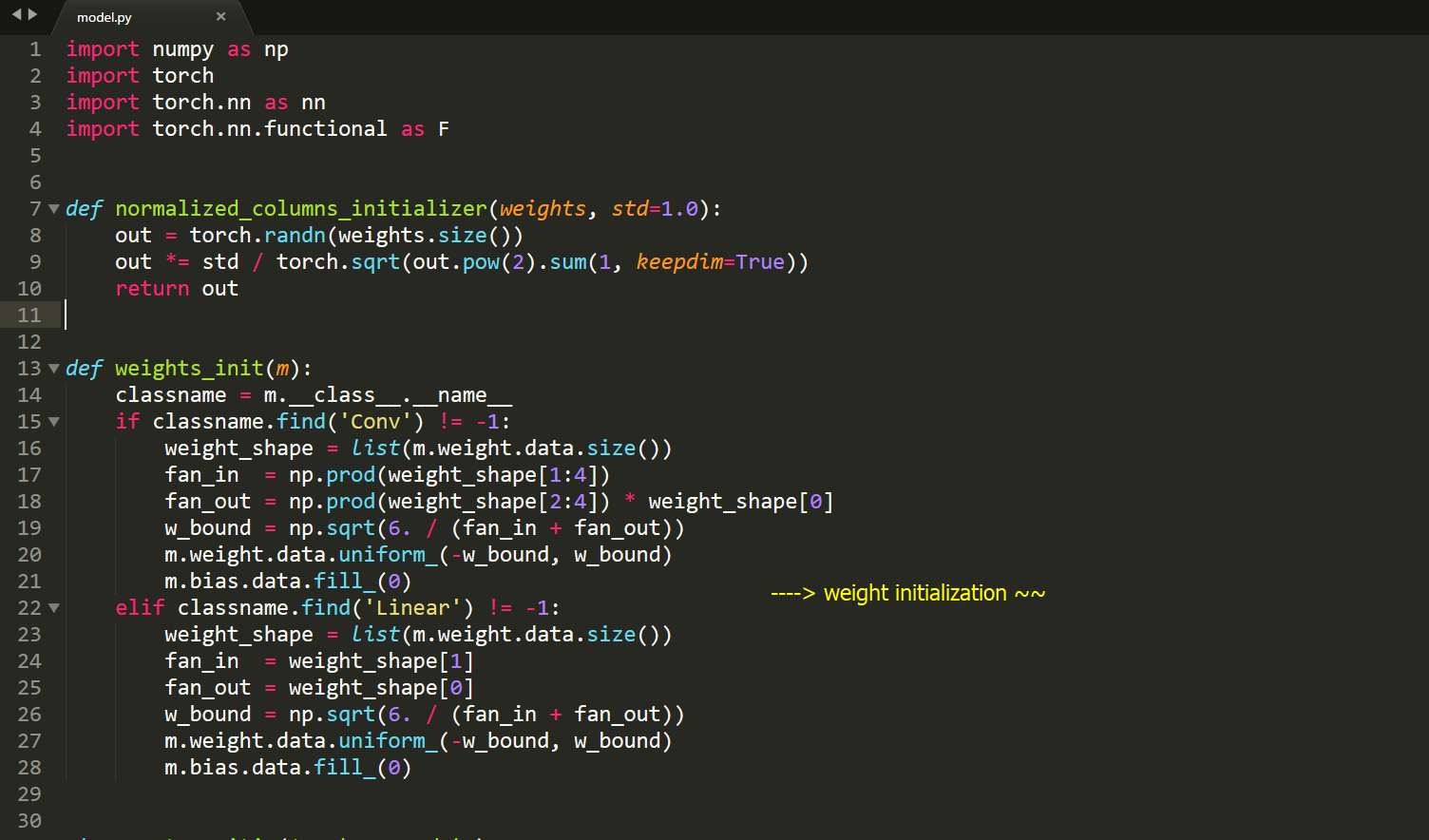
model.py


 浙公网安备 33010602011771号
浙公网安备 33010602011771号