深度学习课程笔记(二)Classification: Probility Generative Model
深度学习课程笔记(二)Classification: Probility Generative Model
2017.10.05
相关材料来自:http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS17.html
本节主要讲解分类问题:
classification 问题最常见的形式,就是给定一个输入,我们去学习一个函数,使得该函数,可以输出一个东西(label)。如下所示:
其实好多其他的问题,都是分类问题演化而来,都可以通过分类问题来解决,如:物体检测,跟踪,分割 等等。。。
那么该怎么执行这个任务呢?万事都是从 training data 说起,我们首先需要收集 训练数据,如下图所示:

收集足够的 training data,这些data 是由 输入 和 输出构成的,即:input 和 label信息。我们可以简单的将分类问题当做回归问题来做。例如:我们要进行二分类的问题,我们可以将 label 1 设置为目标1,label 2 设置为 目标2. 然后测试的时候,根据输出 value 的高低来进行判别。即:如果接近于 1,就认为该类是属于 class 1,接近于 -1,就认为属于 class 2.
那么,可以得到如下的效果:
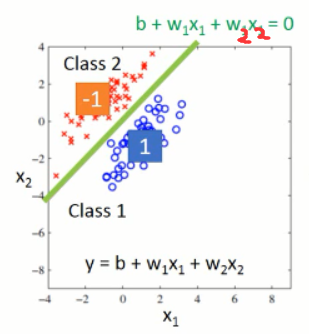
我们只要找到这个分界线即可,使得我们可以将蓝色和红色的数据分布,区分开来。看起来,效果不错的,可以搞。。。但是,实际上,是有问题的。。。有什么问题呢?
因为当蓝色点数据的分布是如下的情况,即:右下角有部分数据,其输出的score 远大于 1,但是回归的目标是,使得蓝色数据的输出向1靠近,那么,这部分蓝色点就会出现 error,那么,模型就会调整分界面,朝着紫色的方向移动,从而使得蓝色数据那部分的score 不是那么的大,从而使得整体的 error 降低。但是这个时候,得到的分界面并不是好的,因为它错误的划分了某些点。
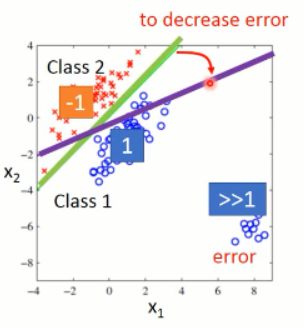
所以,上述例子就说明了,回归问题得到的模型,并不直接适用分类问题。而理想的解决分类问题的流程,应该是这样子滴:

即:我们要找一个 function,该函数能够对于类别1 的输出score 大于0,对于另一个类别,小于 0. 损失函数就是在训练集合中,错误分类的次数。而找这么一个函数的方法有 SVM,Perceptron 等等。但是这次课程,李宏毅老师讲了另外一种方法。什么方法呢?
==================== 分割线 =======================
李宏毅老师先给了一个例子:

告诉你以上信息关于两个盒子中,从 盒子1中取出蓝色球的概率是多少?根据贝叶斯公式,我们可以得到上述公式,然后带进去算一下就得到了。这个看起来,没什么问题。
类似的,我们将两个盒子,换成 两个类别:

那么,给定一个 x,问这个样本属于 class 1 的概率是多少?我们可以用上述公式来完成。但是问题是,我们需要知道右边公式中的每一项的值是多少?我们的任务就是要从 training data 中去学习这些概率,从而完成整个分类问题。
所以,这样子就变成了一个产生式模型(Generative Model)。我们要构建一个这样子的model,使得:
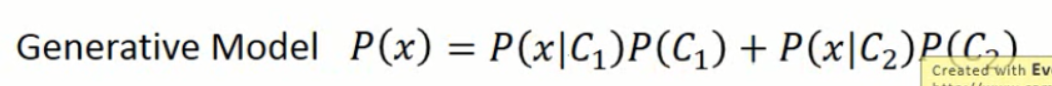
那么,产生出样本 x 的概率是什么呢?就是从类别1中采样出的x的概率乘以从c1中采样出 x 的概率 加上 类型2的概率乘以从类别2中采样出x的概率的加和。这样,我们就可以自己产生 x ,这就是产生式模型。
回到二元分类的问题,我们有两个类别,water 和 normal,那么统计 training data 中这两个类别出现的概率,分别算出来,这个算是先验信息。

那么,问题来了,给定一个海龟,问,该海龟属于 water 的概率是多大呢?我们知道,我们的 sample 都是用 vector 来表示的,那么,我们可以将 water 类别的sample 都可视化出来看看,他们的分布到底是什么样子的呢?

我们简单的用两维的 feature 来可视化这 79种 training sample,可以得到如下的分布图:

那么,其中每一个点,都代表了一个样本,我们可以将其可视化出来看,如:【48,50】代表了是这个鸭子,【65,64】代表了这个站立的乌龟,那么,我们所要猜测的海龟并不在这些 sample 当中,那么它属于 water 类别的概率该怎样计算呢?
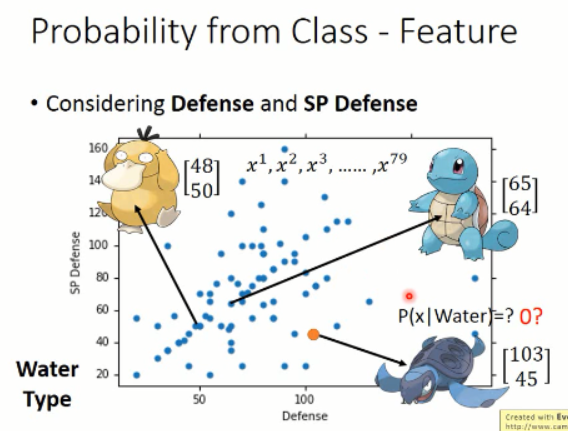
那么,我们将这 79 个样本看做是 所有water class 的冰山一角,而真正的 water 类别是属于一个高斯分布的,而这些样本只是高斯分布采样出来的一点点的样本。
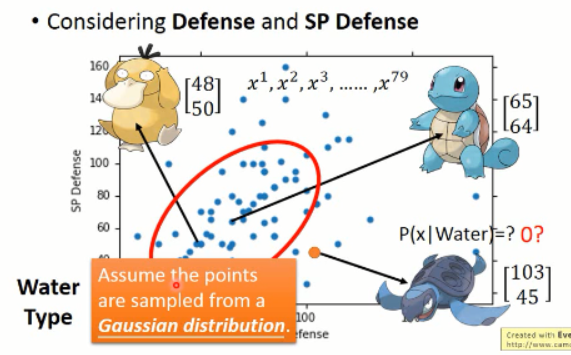
我们怎样才能model出这个高斯分布,才是着重要解决的问题。然后李宏毅老师又讲解了部分高斯分布的知识。看看就可以了,大家都懂吧?
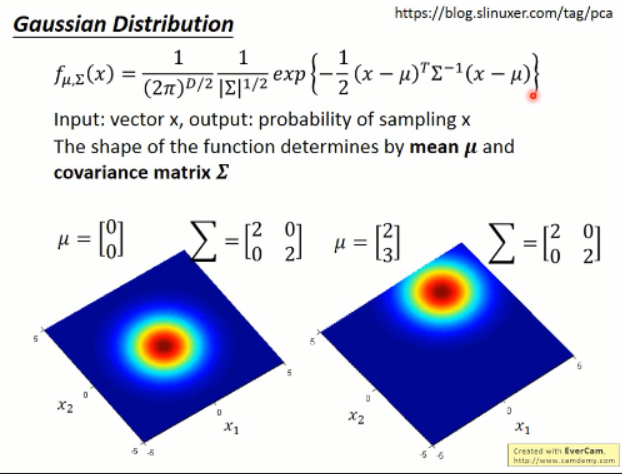
那么,问题继续:假设有了这些样本,我们可以model出一个高斯分布出来,然后只要将 new sample x,带入这个函数就可以得到其属于该高斯分布的概率了。
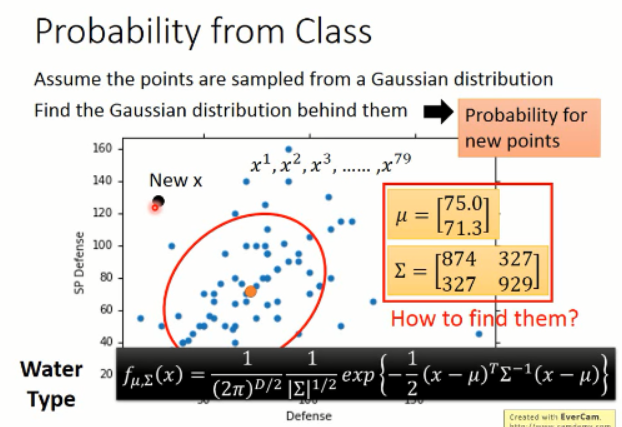
那么,我们怎么找这个 均值和方法呢?使得该高斯分布尽可能好的去model 这些样本?这就要引入最大似然估计了。。。。
如下所示,这些样本可能是任意高斯分布采样出来的,但是不同的高斯分布采样出这些点的似然性是不同的,如:就似然性来说,左下角的那么高斯分布就比右上角的高斯分布要高。
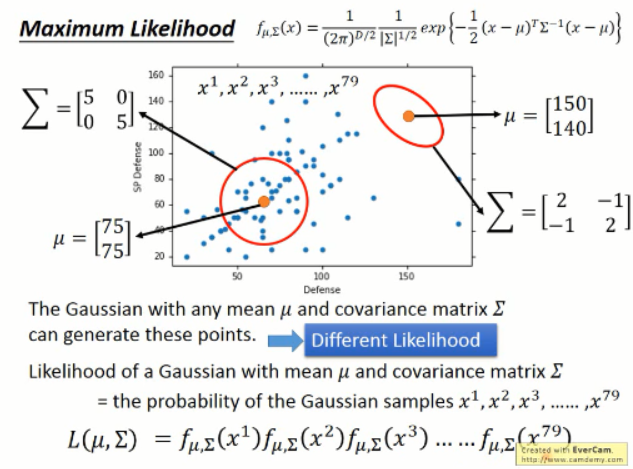
我们该怎么计算这个似然性呢?我们可以将这些点可以看做是独立采样出来的,那么这些点的似然性就是,每一个的概率相乘得到。我们要优化的目标就是,使得找到一组参数,使得该似然性最大:

可以通过微分的方法,来求解出上述结果。有了上面这两个公式,我们将两个类别的数据分别带进去,可以得到:
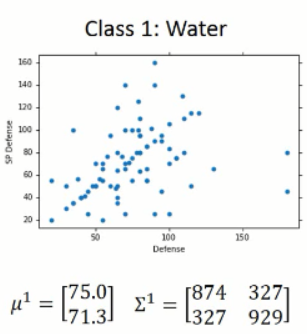
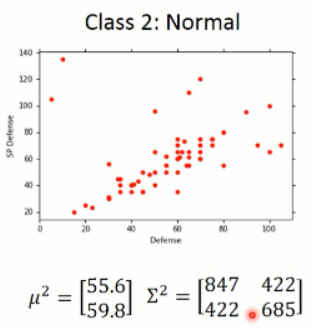
有了这两个高斯分布的情况,我们就可以直接带进去算算就知道分类的情况了。

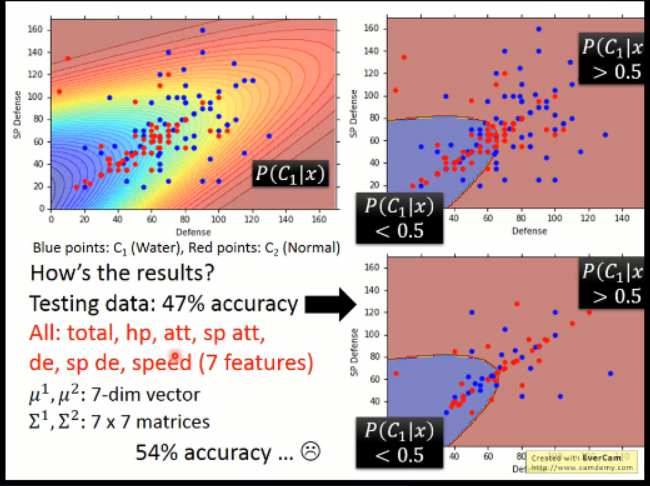
下图是李宏毅老师做的一些实验,上面左上角那个是根据样本得到的概率分布的情况,右上角那个是确定一个边界线之后,在 training data 上的分类情况。可以看到,在两维的情况下,效果不是很好。在测试数据上,只有 47%的精度。
所以,又尝试了 7维的情况,得到了较好结果,但是,依然不是非常好。。。后续会有改进。。。
========================= 分界线 ================================
为了得到更好的结果,我们可以做如下的改动:

我们用参数共享的方法,来做这件事。我们要得到的高斯分布,其均值不变,但是共享方差。所以优化的目标,变成了上述的情况。根据这个计算规则,我们可以得到一组新的高斯分布。
来看看结果怎样吧。

我们可以看到,在我们共享方差之后,这个分界线变成了直线。。。再用了7维的feature之后,其识别精度达到了 73%。。。。可以看到这个提升,还是蛮明显的。
再次回到我们之前说过的三个步骤:
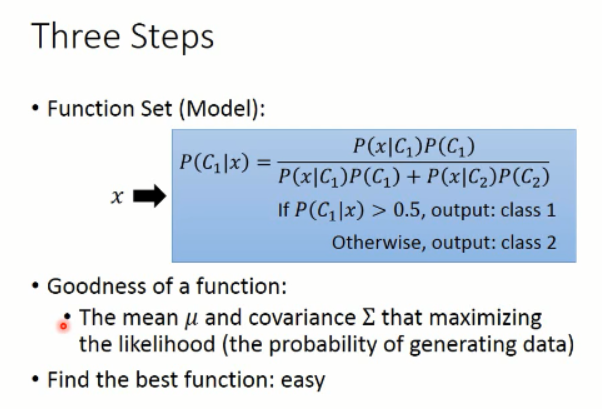
当然,这里概率的选择,不是固定的,你可以选择高斯分布,也可以选择其他的分布。。。

紧接着,我们分析下后验概率:
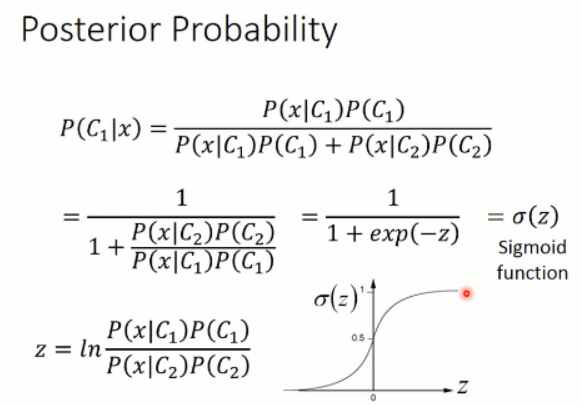
那么,我们继续来看这个关于 z 的 sigmoid 函数:

我们把上面 P(x|c)带入到 z 的函数中去,做相关的整理后,可以得到:

关于 1/2 那一项中的两项,我们可做进一步的展开:
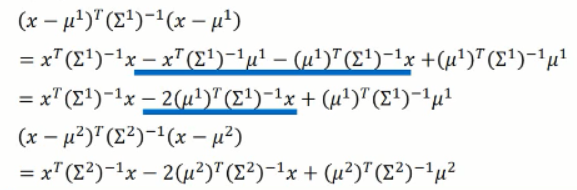
将这两项分别带到上述公式中,我们可以得到 z的新的表达式:
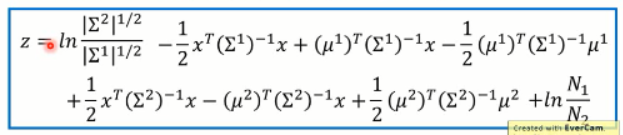
假设这两个方差是相同的,那么我们有:
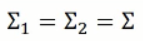
然后上述 z 的函数,可以进一步的简化,我们可以得到:

最终 z 变成了:
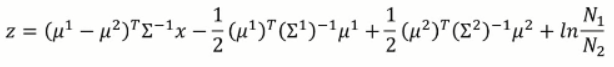
我们有了均值和方差,那么z 函数中的值,都可以用新的标量来表示,即:
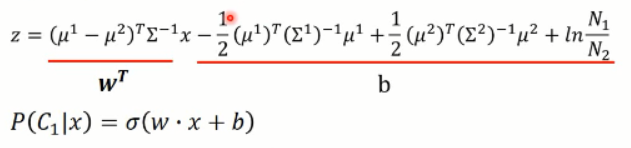
那么,可以看出,这个 z 的函数,其实是一个线性的函数了,这也就解释了为啥之前共享方差后,分界面是一个直线了。还记得吧,看这里:

那么,在产生式模型中,我们所要做的就是算出:

然后,我们就有了 w 和 b。。。。呵呵。 。。。是的,我们类似累活,就是为了算出这两个参数。。。
那么,分类问题,其实不用这么“舍近求远”直接求出 w 和 b 不就可以了吗?是的啊,我们下节课再说吧。。。哈哈。。。。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号