论文笔记之:Hybrid computing using a neural network with dynamic external memory
Hybrid computing using a neural network with dynamic external memory
Nature 2016
updated on 2018-07-21 15:30:31
Paper:http://www.nature.com/nature/journal/vaop/ncurrent/pdf/nature20101.pdf
Code:https://github.com/deepmind/dnc
Slides: http://people.idsia.ch/~rupesh/rnnsymposium2016/slides/graves.pdf
Blog:
1. Offical blog: https://deepmind.com/research/dnc/
2. others:
- https://greydanus.github.io/2017/02/27/differentiable-memory-and-the-brain/
- https://nbviewer.jupyter.org/github/greydanus/dnc/blob/master/free-recall/free-recall-rnn.ipynb
- https://zhuanlan.zhihu.com/p/33852794
Applications on CV tasks (for example, 3 CVPR-2018 papers):
2. One-Shot Image Recognition: http://openaccess.thecvf.com/content_cvpr_2018/papers/Cai_Memory_Matching_Networks_CVPR_2018_paper.pdf
3. Video Caption: http://openaccess.thecvf.com/content_cvpr_2018/papers/Wang_M3_Multimodal_Memory_CVPR_2018_paper.pdf
摘要:人工智能神经网络 在感知处理,序列学习,强化学习领域得到了非常大的成功,但是限制于其表示变量和数据结构的能力,长时间存储知识的能力,因为其缺少一个额外的记忆单元。此处,我们引入一个机器学习模型,称为:a differentiable neural computer (DNC),包含一个 神经网络,可以读取和写入一个额外的记忆矩阵;类似于计算机当中的 random-access memory。像传统的计算机一样,可以利用其 memory 表示和执行一个复杂的数据结构,但是,像神经网络一样,也可以从数据中进行学习。当进行监督学习的时候,我们表明 一个 DNC 能够成功的回答模拟的问题,在自然语言中进行推理和论证问题。我们表明,他可以学习到类似 给定特定点的最短距离 和 推理在随机产生的图中丢失的连接,然后推广到特定的 graph,例如:交通运输网络 和 家谱树结构。当进行强化学习的时候,一个 DNC 可以完成移动 block 的难题。总的来说,我们的结果表明,DNCs 能够解决复杂的,结构化的任务,但是这些任务假如没有 external read-write memory,那么根本无法完成的任务。
引言:
虽然最近的突破表明神经网络在信号处理,序列学习,强化学习上有很强的适应性。但是,认知科学家和神经科学家都认为:神经网络在表示变量和数据结构上,能力有限,以及存储长时间的数据(the neural networks are limited in their ability to represent variables and data structure, and to store data over long timescales without interference)。我们尝试结合神经元和计算处理的优势,具体做法是:providing a neural network with read-write access to exernal memory. 整个系统都是可微分的,可以用 gradient descent 的方法进行 end to end 的学习,允许网络自动学习如果操作和组织 memory(in a goal-directed manner)。
System Overview:
A DNC is a neural network coupled to an external memory matrix.
如果 memory 可以认为是:DNC's RAM,那么,the network,可以认为是 controller,是一个可微分的 CPU,其操作是用 gradient descent 的方法来学习的。DNC 的结构不同于最近的神经记忆单元,主要体现在:the memory can be slectively written to as well as read, allowing iterative modification of memory content.
传统的计算机利用独特的地址俩访问 memory content,DNC 利用可微分的注意力机制来定义:distributions over the N rows, or "locations", in the N*M memory matrix M. 这些分布,我们称之为:weightings,代表了每个位置涉及到 read or write operation 的程度。

这些功能性的单元,决定和采用了这些权重,我们称之为:“read and write heads”。heads 的操作,如图1所示。
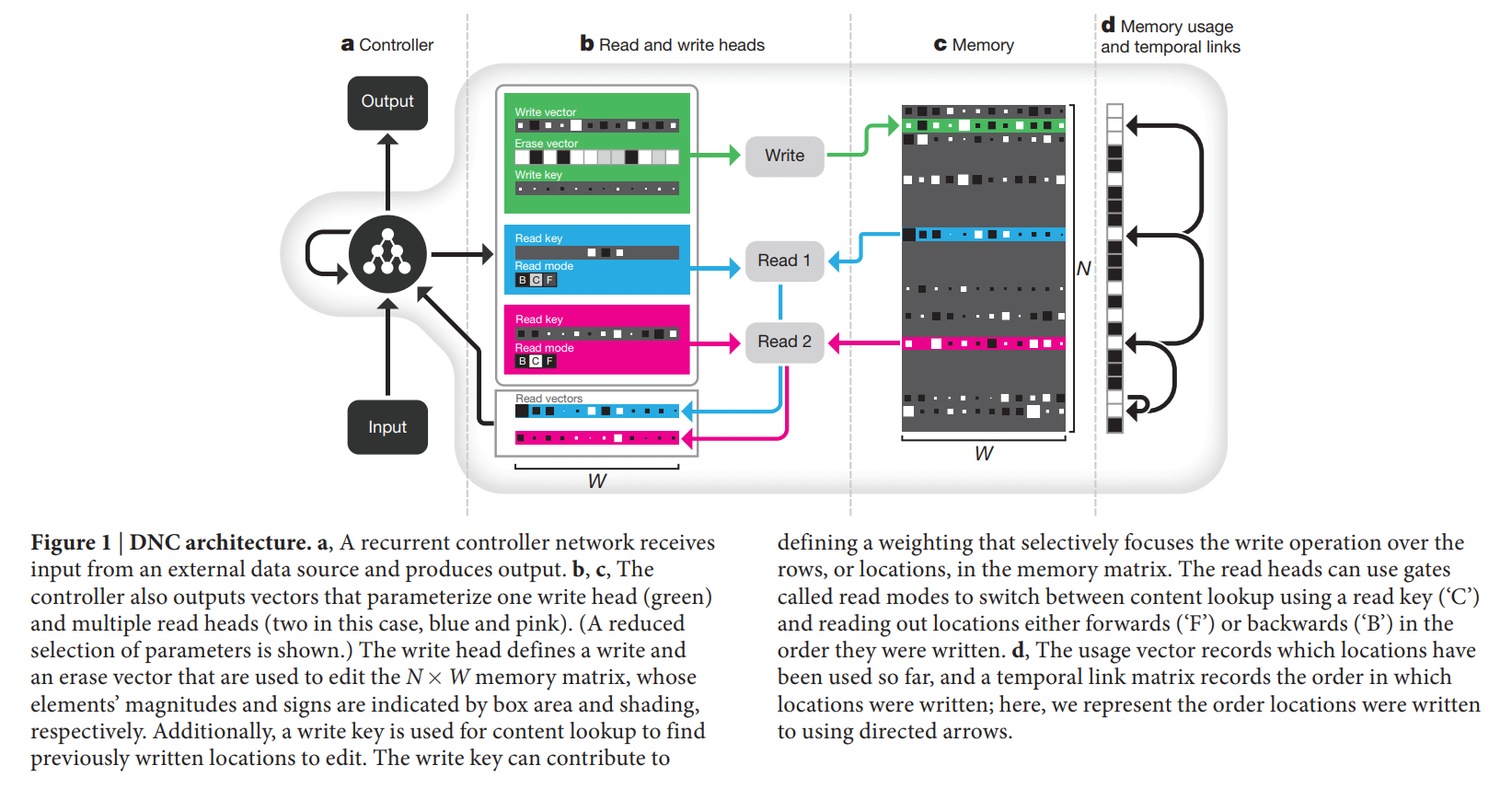
Interaction between the heads and the memory
The heads 利用了三种不同形式的可微分的 attention。
第一种是:the content lookup (内容查找表), in which a key vector emitted by the controller is compared to the content of each location in memory according to a similarity measure (here, cosine similarity).
第二种 attention 机制记录了:records transitions between consecutively written locations in an N*N temporal link matrix L.
第三种 attention 分配内存用于 writting。
注意力机制的设计是受到计算上的考虑。
Content lookup 确保了连接数据结构的形式;
temporal links 确保了输入序列的时序检索;
allocation 提供了 the write head with unused locations.
METHODS
Controller Networks.
在每一个时间步骤 t 控制网络 N 从数据集或者环境中接收一个输入向量 xt,并且输出一个向量 yt 用于参数化要么是一个目标向量 z 的预测分布(监督学习的角度来说),要么是一个动作分布(强化学习的角度来说)。另外,the controller 接收一组 R read vectors from the memory matrix Mt-1 at the previous time-step, via the read heads. 它然后发射一个 interface vector,定义了在当前时刻与 memory 的交互。为了符号表示的方便,我们将输入和 read vectors 表示为 a single controller input vector Xt = [xt; rt-11; ... ; rt-1R]. 任何结构的神经网络都可以用于 controller,但是我们这里采用 deep LSTM 结构的变种:
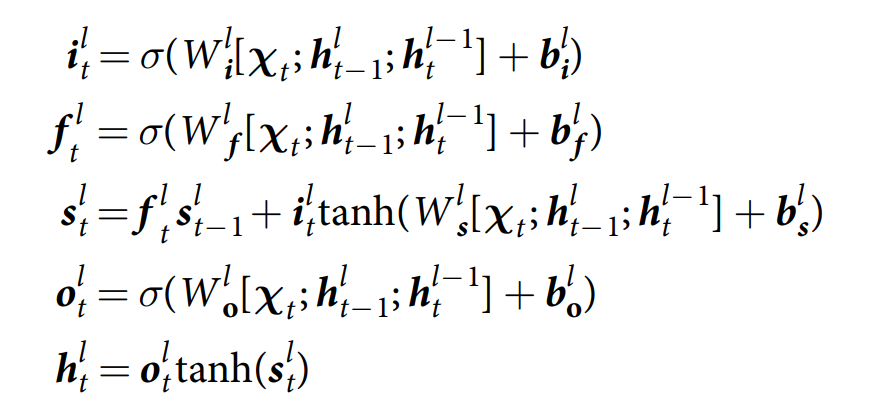
其中,i,f, s, o, h 分别代表输入门,遗忘门,状态(即常规的cell),输出门,以及 hidden state。
在每一个时间步骤,the controller 发射一个 输出向量 vt,以及一个交互向量,定义为:
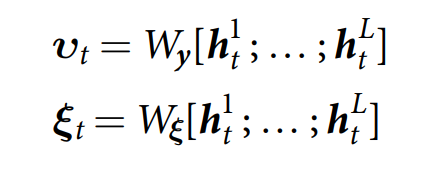
假设控制网络是 recurrent,他的输出是复杂历史(X1, X2, ... Xt)的函数。所以我们可以压缩 the controller 的操作为:
![]()
It is possible to use a feedforward controller, in which case N is a function of Xt only; however, we use only recurrent controller in this paper.
最终,输出的向量 yt 定义为:adding vt to a vector obtained by passing the connection of the current read vectors through the RW*Y weight matirx Wr:
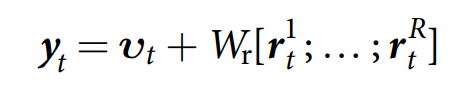
这种安排使得 DNC 能够在刚刚读取到的记忆基础之上,进行决策的输出;但是很难将这个信息传递到 controller,从而利用他们来决定 v,without carrying a cycle in the computation graph.
Interference parameters:
Before being used to parameterize the memory interactions, the interface vector 被划分为如下几个部分:
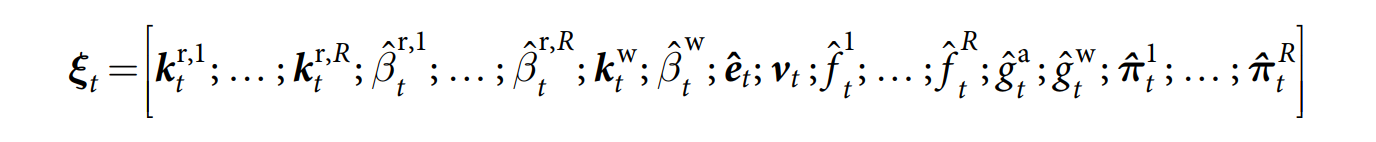
每一个单独的成分然后被不同的函数进行处理,以确保他们能够在合适的 domain 当中。如:
1. the logistic sigmoid function is used to constrain to [0, 1].
2. the "oneplus" function is used to constrain to [1, 无穷),其中:
oneplus(x) = 1 + log(1+ex)
3. softmax function is used to constrain vectors to SN, the N-1-dimensional unit simplex:
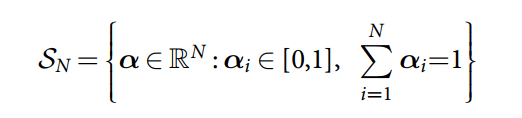
在处理完毕之后,我们有如下的变量和向量:
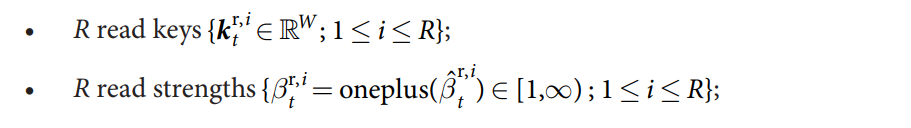
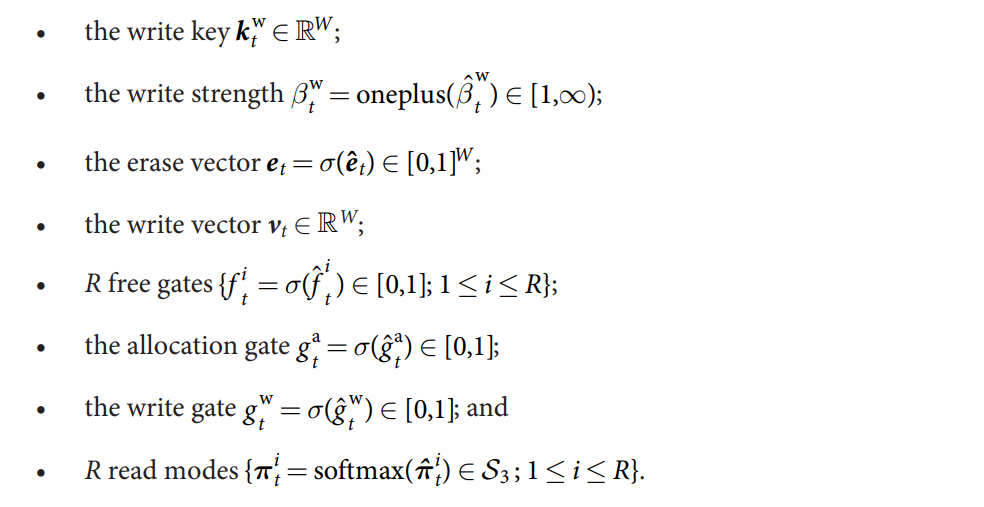
Reading and Writing to memory
选择位置进行读写是依赖于权重(weighting)的,即:属于0-1之间的 value,总和为 1. The complete set of allowed weightings over N locations is the non-negative orthant of RN with the unit simplex as a boundary (known as the "corner of the cube"):
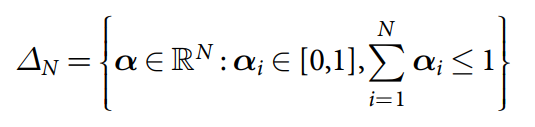
对于 read 操作,R read weightings ![]() 被用于计算内容的加权平均,所以,定义 read vectors
被用于计算内容的加权平均,所以,定义 read vectors ![]() 为:
为:
![]()
The read vectors 加上 下一个时间步骤的 controller input,使之能够访问到 memory content。
The write operation 被单个 write weighting 所调节,经常跟擦除向量(erase vector)和 写入向量(write vector)一起使用来修改记忆:
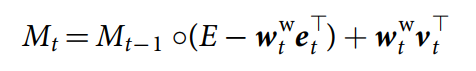
其中,E 是 N*W matrix of ones.
Memory Addressing:
这个系统利用了 content-based addressing and dynamic memory allocation to determine where to write in memory ;
content-based addressing and temporal memory linkage to determine where to read.
下面将分别介绍这些机制:
Content-based addressing. 所有的 content lookup 操作,都利用如下的函数:
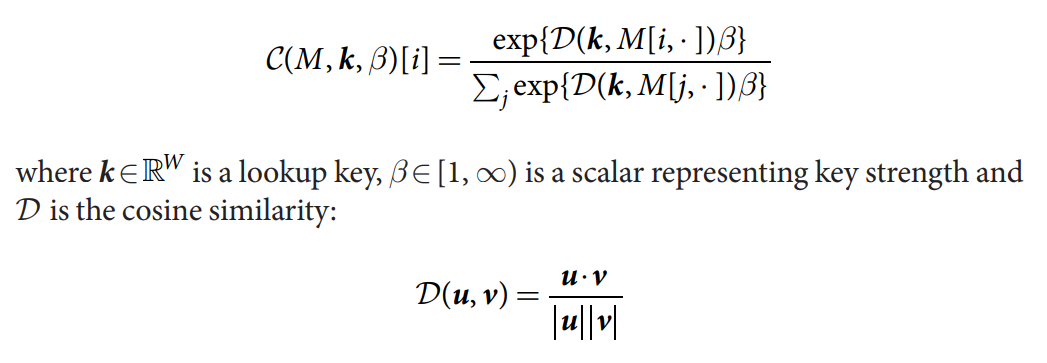
权重 $C(M, k, \beta)$ 定义了一个归一化的概率分布(over the memory locations)。
Dynamic memory allocation. 为了允许 the controller 能够释放和分配所需要的 memory,我们研发了一个可微分的类似 “free list” 的 memory allocation scheme,其中,可用记忆位置的列表(a list of available memory locations)是通过添加和移除 linked list 上的 address 来实现的。在时刻 t 的记忆利用向量为:ut, 并且 u0 = 0。在写入到 memory 之前,the controller 发射一系列的 free gates,one per read head, 来决定是否最近读取的位置可以被释放?The memory retention vector 表示 how much each location will not be freed by the free gates, 并且定义为:
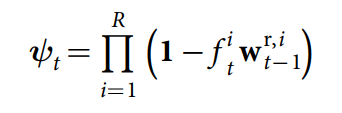
所以,the usage vector 可以定义为:
![]()
直观上的理解:locations are used if they have been retained by the free gates, and were either already in use or have just been written to. 每一次对一个位置的写入,都会增加他的 usage,直到1,利用率也可以用过 free gates 进行逐渐的降低;ut 的元素从而可以被约束在 [0, 1]之间。一旦 ut 被确定了,the free list ![]() 就被定义为:sorting the indices of the memory locations in ascending order of usage; 对应的,
就被定义为:sorting the indices of the memory locations in ascending order of usage; 对应的,![]() 就是 the index of the least used location。分配的权重 at 被用于提供新的位置来进行写操作,即:
就是 the index of the least used location。分配的权重 at 被用于提供新的位置来进行写操作,即:
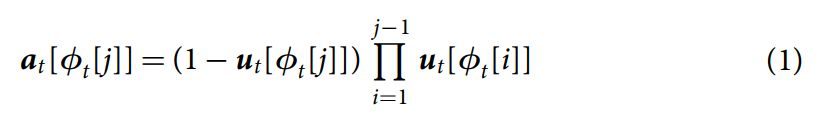
如果所有的 usage 都是1,那么 at = 0 ,the controller 就不在能够分配 memory了,除非它首先将已经使用的 locations 进行释放.
Write weightings:控制器可以写入到 newly allocated locations,或者 locations addressed by content, 或者他可以选择不进行 write 操作。首先,一个写入内容权重通过 the write key 和 write strength 来构建:
![]()
其中,ctw is interpolated with the allocation weighting at defined in equation (1) to determine a write weighting:
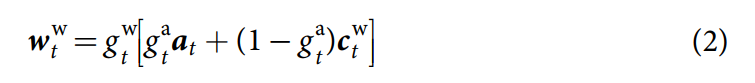
其中,gta is the allocation gate governing the interpolation and gtw is the write gate. 当 write gate 为 0 的时候,然后就什么都不进行写入,而不管其他参数怎么样;这可以从某种程度上保护记忆,免得受到不必要的更新。
Temporal memory linkage:The memory allocation system 不存储序列信息(stores no information about the order )。 但是,这种次序的信息却经常是有效的:for example,when a sequence of instructions must be recored and retrieved in order. 所以,我们采用了一个 link matrix L 来跟踪连续被修改的记忆位置(to keep track of consecutively modified memory locations)。
Lt [i, j] represents the degree to which location i was the location written to after location j, and each row and column of Lt defines a weighting over locations: ![]()
为了定义 Lt, 我们需要 a precedence weighting Pt, where element Pt[i] represents the degree to which location i was the last one written to. Pt is defined by the recurrence relation:
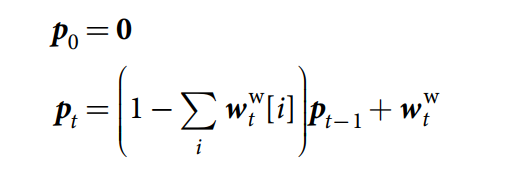
每次当一个位置被更新之后,the link matrix 被更新,to remove old links to and from that location. 从上次写入的位置的新的链接被添加。我们利用如下的 recurrence relation 来执行这个逻辑:
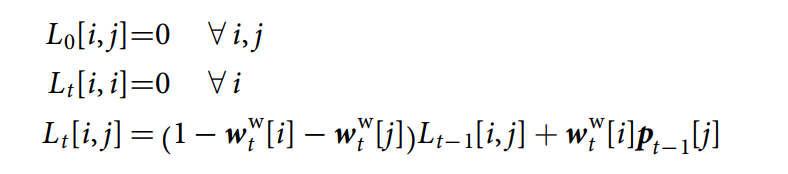
我们将 self-links 扔掉了(即:link matrix 的对角线元素全部为 0),因为:it is unclear how to follow a translation from a location to itself. Lt 的行和列分别代表了:temporal links 进去和出来某一特定 memory slots 的权重。给定 Lt,read head i 的反向权重 bti 和前向权重 fti 分别定义为:
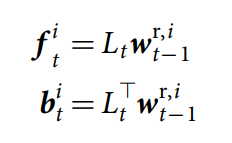
其中,![]() 是第 t-th 次从上一个时间步骤得到的 read weighting。
是第 t-th 次从上一个时间步骤得到的 read weighting。
Sparse link matrix. the link matrix is N*N and therefore requires O(N2) resources in both memory and computation to calculate exactly.

Read weighting.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号