论文笔记之:Human-level control through deep reinforcement learning
Human-level control through deep reinforcement learning
Nature 2015 Google DeepMind
Abstract
RL 理论 在动物行为上,深入到心理和神经科学的角度,关于在一个环境中如何使得 agent 优化他们的控制,提供了一个正式的规范。为了利用RL成功的接近现实世界的复杂度的环境中,然而,agents 遇到了一个难题:他们必须从高维感知输入中得到环境的有效表示,然后利用这些来将过去的经验应用到新的场景中去。显著地,人类和其他动物看起来可以通过一个和谐的RL 和 层次感知处理系统的有效组合进而解决这个问题。前者通过丰富的神经数据解释了由
The Methods:
Preprocessing:直接处理 Atari 2600 帧,图像大小是 210*160。我们为了降低输入的维度,采取了一个基础的预处理的步骤,用 Atari 2600 仿真器来进行人为处理。首先,为了编码单张图像,我们采用当前编码帧和前一帧每一个像素点色彩值的最大值。移除闪烁是很有必要的,因为一些物体仅仅出现在奇数帧,而有一些则只出现在偶数帧,由于有限数量的精灵导致的 artefact 会立马显现。 第二,我们然后提取 Y 通道,也就是经常说的 亮度,然后将其resize成 84*84的。
Code availability. 代码链接:https://sites.google.com/a/deepmind.com/dqn
Model architecture. 利用神经网络,有好几种不同的方法来参数化 Q。因为 Q 映射了 历史-动作对(history-action pairs)到他们的Q值,历史 和 动作 已经在之前的方法中被用于神经网络的输入。这种结构的主要缺点是:一个单独的前向传播需要计算每一个动作的Q值,导致计算代价和动作的数量成比例上升。我们则使用这样的一个结构,即:每一个可能的动作有一个单独的输出,仅仅将状态表示输入给神经网络。输出对应了每一个动作为每一个状态预测的Q值。这种结构的优势是:在一个给定的状态下,对于所有可能动作的Q值的计算,在网络中仅仅需要一个前向传播即可。
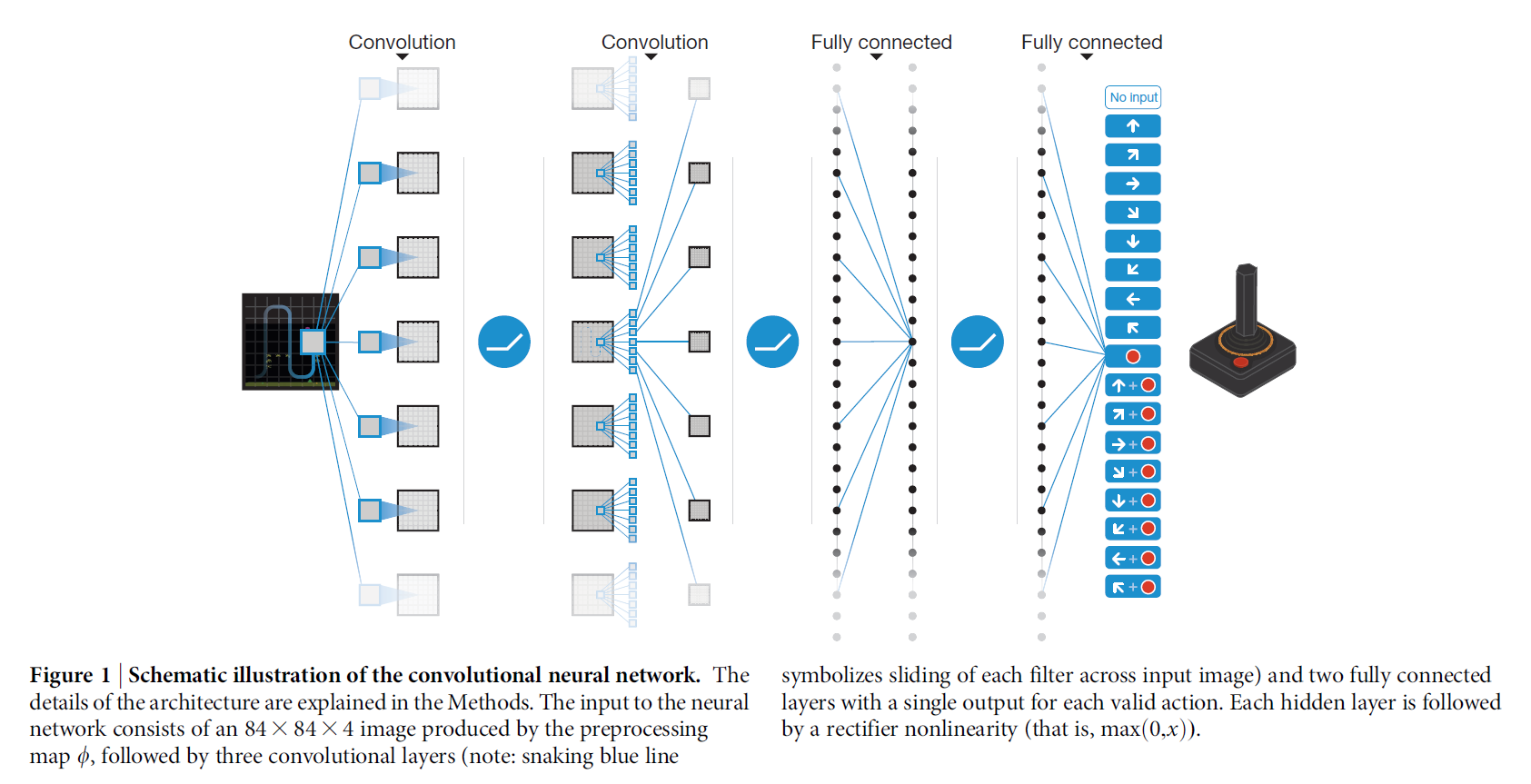
图1中展示的结构,给出如下的描述:传入给神经网络的输入是预处理映射完毕后的 84*84*4 的图像。
第一个隐层:卷积核大小为 8*8 , 然后有 32个filter,步长为4;后面跟一个非线性激活函数;
第二个隐层:卷积核大小为 4*4, 然后有 64个filter,步长为2;后面跟一个非线性激活函数;
第三个卷积层,64个filter,卷积核大小为 3*3,步长为1,后面也跟着一个 rectifier;
最后的隐层是:全连接层,由512个rectifier units 构成;
输出层是 一个全连接,每一个有效地动作对应一个输出。
作者考虑在游戏中,有效动作的数量 从4~18之间变换。
Training details:
每一个游戏,一个网络:所有的游戏都用同样的网络结构,学习算法,以及超参数设置。由于游戏的分数都不一样,所以作者将所有的 positive reward 设置为1,negative reward 设置为 -1,不变化的则设置为0.
训练过程中行为策略是 贪心算法。
像之前的算法一样,本文也是采用 跳帧技术,即: the agent 看并且选择动作每隔 k 帧,而不是每一帧都做。其最后一个动作在跳过的帧上重复。
Algorithm:
我们考虑这样的任务,在一个由动作,观察 和 奖励构成的序列中,agent 和环境交互。每一个时间步骤, the agent 从合法的游戏动作中选择一个动作 $a_t$。然后将此动作传输给模拟器,以修改其内部状态 和 游戏得分。总的来说,该环境可能是随机的。agent 看不到模拟器的内部状态;但是可以看到从模拟器传来的图像,即:代表当前屏幕图像信息的由像素构成的向量。此外,其还接收到代表游戏得分变换的奖励 $r_t$。既然总的来说,游戏得分可能依赖于之前序列的动作和观察;关于某动作的反馈,可能经过几千次的时间步骤才会接收到。
因为 agent 仅仅观察到当前的屏幕,所以该任务是部分观测的,许多模拟器的状态是有感官上的锯齿现象的(即,仅仅从当前屏幕 $x_t$ 不可能完全的明白当前的情况)。所以,动作和观察的序列,$s_t = x_1, a_1, x_2, ... , a_{t-1}, x_t$, 输入给算法,然后依赖于这些序列进行游戏策略的学习。模拟器中的所有序列,都假设会在有限时间步骤内结束。这种形式就构成了一个大而有限的 马尔科夫决策过程(MDP),其中的每一个序列都是单独的状态。简单地将完整的序列 $s_t$ 作为第 t 个时刻的状态描述。
agent 和 模拟器交互的目标是能够获得最大的累积奖励。我们做出一个标准的假设,即:奖励的奖励都被一个衰减因子 $\gamma$ 相乘,(设置 $\gamma = 0.99$),定义时刻t的折扣反馈为:
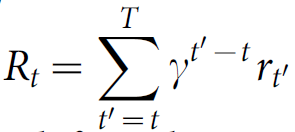
其中,T 是游戏结束的时刻。
我们定义 最优的 动作-值函数 $Q^*(s, a)$,作为最大的期待反馈,在观察了一些序列 s 之后,然后才去一些动作 a, $Q^*(s, a) = max_{\pi} E[R_t|S_t = s, a_t = a, \pi]$,其中 $\pi$ 是映射序列到动作的一个策略。
最优的动作-值函数遵循一个重要的等式,即:贝尔曼等式(Bellman equation)。这是基于如下的观察:如果序列 s‘ 在下一个时间步骤最优的值 $Q^*(s', a') $ 对于所有动作 a’ 来说都是已知的,那么最优的策略应该是选择这么一个动作 a',从而可以得到最大的期望值 $r + \gamma Q^*(s', a')$:
$Q^*(s, a) = E_{s'}[r + \gamma max_{a'} Q^*(s', a')|s, a]$
许多RL 算法基本的idea都是:利用贝尔曼等式来预测 动作-值函数 作为一次迭代更新,$Q_{i+1}(s, a) = E_{s'}[r + \gamma max_{a'} Q_i(s', a')|s, a]$。随着 i 趋于无穷大,这样的值迭代算法收敛到最优动作值函数,$Q_i -> Q^*$。实际上,这些基础的方法是不切合实际的,因为每一个动作值函数分别预测给每一个序列,没有任何 generalization。 实际上,用一个函数估计来预测 动作值函数是很common的。在RL领域经常利用线性函数逼近器,有时候也会用非线性函数,如:神经网络。我们提到 带权重的神经网络函数逼近器称为:Q-network。一个Q-network 可以通过在第 i 次迭代来调整参数 $\theta_i$而得到训练,以此降低贝尔曼等式中的均方误差 (mean-squared error),其中最优目标值 $r + \gamma max_{a'}Q^*(s' , a')$ 利用之前一些迭代得到的参数 $\theta_i^-$ 替换为估计目标值 $y = r + \gamma max_{a'}Q(s', a'; \theta_i^-)$。这就会使得 损失函数 $L_i(\theta_i)$ 的序列随着迭代次数 i 而改变:
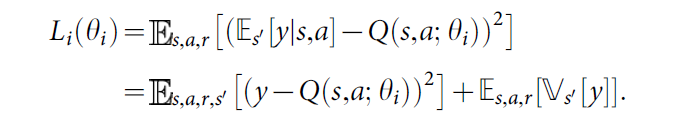
注意到,目标依赖于网络的权重;而有监督的学习,在学习开始之前是固定的。在每一个优化阶段,当优化第 i 个损失函数 $L_i(\theta_i)$时,固定之前迭代的参数 $\theta_i^-$,就会有一系列定义好的优化问题。最后一项是 目标的方差,不依赖于我们当前优化的参数 $\theta_i$,所以可以暂时忽略。区分不同的损失函数及其对应的权重,我们有如下的梯度:

注意到,本文的算法是:model-free and off-policy。
Model-free:因为本文算法是直接从模拟器中得到的样本来解决强化学习任务,而没有显示的预测奖赏和转移概率 $P(r, s'|s, a)$。
Off-policy:学习贪婪策略 $a = argmax_{a'} Q(s, a'; \theta)$,与此同时,采用一个确保有足够状态空间探索的行为分布。实际上,该行为分布是经常被选中通过一个 $\epsilon-greedy$ 策略,有 $1-\epsilon$的概率来选择一个贪婪策略,有 $\epsilon$ 的概率随机的选择一个 action。
其实,off-policy 更主要的是讲:策略评估 和 策略改进的不是同一个策略。例如:Q-learning 评估的是 贪心策略,而改进的是 原始策略(即,没有采用贪心算法策略)。这里比较容易懵逼啊。。。呃呃呃。。。
Training algorithm for deep Q-networks.
训练深度 Q-network 的算法在 Algorithm 1中。基于Q,根据 贪心策略来指导 agent 选择和执行动作。由于,将任意长度的历史作为神经网络的输入是有困难的,我们的 Q-function 作用于 利用上述函数 产生的固定长度表示的历史。该算法从两个角度 修改了 Q-learning,使其适合大型神经网络的训练并且不会发散。
首先,我们利用称为 Experience Replay 的技术,存储每一个时间步骤 agent的经历,$e_t = (s_t, a_t, r_t, s_{t+1})$,在该算法的内部循环中,我们对 experience 样本 采用 Q-learning 更新,或者 minibatch updates,$(s,a,r,s') ~ U(D)$,从存储的样本池子中随机的抽取。
该方法对比传统的 online Q-learning算法有以下几个优势:
1. Experience 的每一个步骤经常用到许多权重更新中去,允许更好的数据效率。
2. 由于样本之间强烈的相关性,直接从连续的样本中进行学习是 inefficient的;样本的随机化破坏了该相关性,从而减少了更新的方差。
3. 当 on-policy 的学习时,当前的参数决定了用来训练参数的下一个数据样本。(when learning on-policy the current parameters determine the next data sample that the parameters are trained on.)
例如:如果最大动作是向左移动,然后训练样本就由左边的样本主宰;如果向右移动,训练样本的分布也会交换。
很容易发现,不想要的反馈循环(feeback loops)是如何产生的,参数也可能在一个 poor 的局部最小困住,或者直接就悲剧的发散了。
第二个改动是:
为了改善我们方法的稳定性,在 Q-learning 更新的过程中,我们使用了额外的 目标网络(target network)来产生目标 $y_j$。
确切的讲,每执行 C 次迭代,我们将网络 Q 克隆下来,然后得到一个目标网络(target network Q'),然后用这个目标网络Q' 来在接下来的 C 次迭代中来产生 Q-learnng的目标 $y_j$。这个改变,使得算法相对标准的 online Q-learning 来讲,更加稳定,因为 普通的 Q-learning 一次更新增加了 $Q(s_t, a_t)$ 经常对于所有的 a 来讲,也增加了 $Q(s_{t+1}, a)$,所以就增加了目标 $y_j$,可能会导致震荡或者策略的发散。用一组较老的系数来产生 target,增加了 更新Q的时间 和 更新能够影响到目标 $y_j$ 的时间的延迟,使得不容易发散。
还有一个“黑科技”,即:
此外,作者还发现将更新 限制在 -1 到 1之间 能够提升算法的有效性。因为所有的 |x| 的 positive value 的梯度是1,而 negative value 的值为 -1,将平方差剪切到 -1 和 1 之间就对应了 利用一个绝对值损失函数来处理 在(-1,1)间隔之外的误差(error )。这种 error clipping 方式进一步的改善了算法的稳定性。
总的算法流程如下:



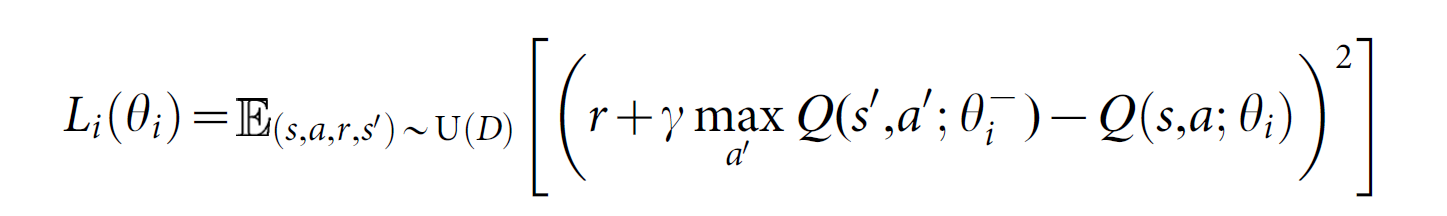

 浙公网安备 33010602011771号
浙公网安备 33010602011771号