How NAS was improved. From days to hours in search time

2020-03-29 21:18:08

Source: https://medium.com/peltarion/how-nas-was-improved-from-days-to-hours-in-search-time-a238c330cd49

Neural Architecture Search(NAS) has revolutionized the process of constructing new neural network architectures. Using this technique it is possible to automatically find an optimal neural network architecture for a specific problem. What’s more? The definition of optimal can be adjusted to model a tradeoff between multiple features, such as size of the network and accuracy[1]. What’s even more impressive is the fact that NAS can now be performed within only a few hours on a single GPU instead of 28 days on 800 GPUs. This leap in performance has only taken an astonishing two years and now you don’t need to be a Google employee anymore to use NAS.

But how have researchers been able to achieve this leap in performance? In this article I’ll go through the new ideas that helped pave the way for this success story.

The Catalyst

The story of NAS started back in 1988 with the idea of self-organizing networks[2], but it wasn’t until 2017 that the first major breakthrough was made. This was when the idea of training a recurrent neural network(RNN) to generate neural network architectures was presented.

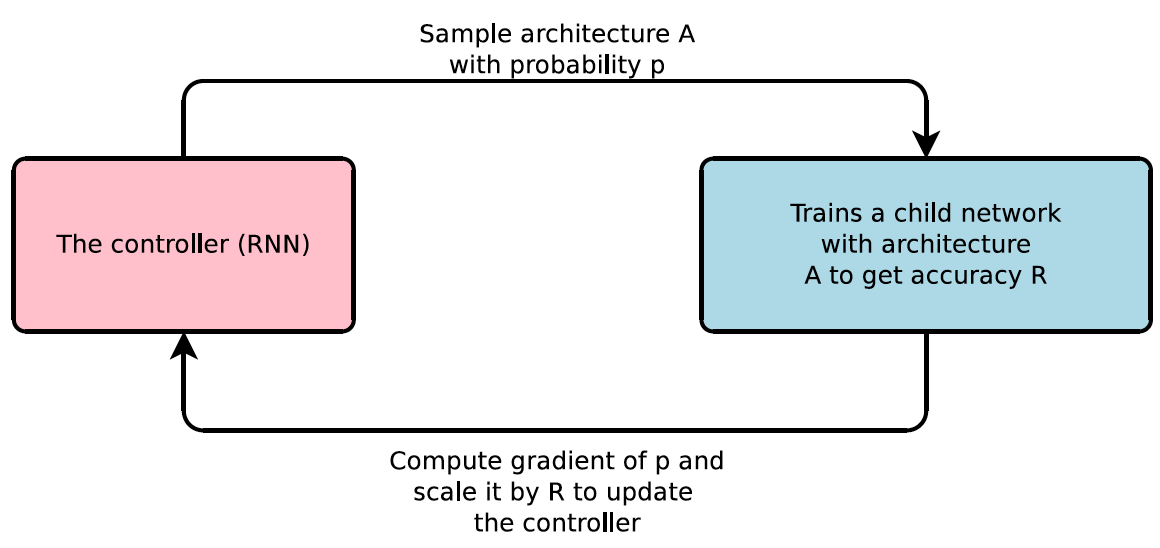
Figure 1: an overview of the iterative process of training the NAS controller.

In simple terms the process is very reminiscent of how a human would try to find the best architecture. Based on a defined search space of the most promising operations and hyperparameters, the controller will test different neural network configurations. In this context testing a configuration means to assemble, train and evaluate a neural network in order to observe its performance. Then, after many iterations, the controller will learn which configurations make up the best neural networks within the search space. Unfortunately, just as for a human, the number of iterations required to find the best architecture within a search space is extremely large, making it a slow process. This is partly because the search space is suffering from combinatorial explosion; meaning that the number of possible networks in the search space increases greatly with the number of components added to the search space. However, this approach was indeed able to find a state-of-the-art(SOTA) network that is now commonly known as NASnet[3], but that required 28 days on 800 GPUs. Such high computational costs make the search algorithm impractical to utilize for most people.

So how can this idea be improved in order to make it more accessible? In the NAS process the majority of the time comes from training and evaluating networks that are suggested by the controller. Utilizing multiple GPUs makes it possible to train models in parallel, but their individual training time is still quite slow. A reduction in the computational cost of training and evaluating the neural networks would have a big impact on the total search time of NAS.

This leads to the question, how does one reduce the computational cost of training and evaluation neural networks without negatively impacting the NAS algorithm?

Lower Fidelity Estimates

A commonly known correlation is that smaller neural networks are faster to train than larger ones; for the simple reason that the computational cost is less in smaller networks. However, smaller neural networks usually achieve poorer performance than larger neural networks, in accuracy. The goal of NAS is to find SOTA network architectures; is there a way to use smaller models within the search algorithm without sacrificing the final performance?

Figure 2: Example ResNet architecture where the residual blocks are presented as “ResNet Block”.

The answer to that question can be found in one of the most well known computer vision architectures, ResNet[4] . In the ResNet architecture one can observe that the same set of operations is being repeated over and over. These operations form the residual block, which is the building block of ResNet. This design pattern enables the possibility of creating deeper or shallower variants of the same model through varying the number of stacked residual blocks. The assumption in this architectural design is that a well constructed building block can be iteratively stacked to create high performing larger nets, which fits NAS perfectly. In the context of NAS this means it is possible to train and evaluate small models while being able to scale up the neural network later. This is analogue to conducting NAS on a ResNet18, then building a ResNet50 by repeating the resulting block.

Searching for a building block instead of an entire architecture, as well as training and evaluating smaller models, resulted in a huge speed up, achieving search times of 3–4 days using 450 GPUS[5]. Furthermore, the technique is able to find SOTA architectures even though only building blocks are being searched for.

However, despite this being a huge improvement, the process is still quite slow and the number of GPUs required needs to be decreased before it is realistic to apply it in practice. Training neural networks from scratch will always be a time consuming process, no matter the model size; is there perhaps a way to reuse the weights from the previously trained networks?

Weight inheritance

How does one avoid training a neural network from scratch? The short answer to that is by using weight inheritance, i.e. borrowing weights from another network that has already been trained. In NAS the search is conducted on a specific target dataset and multiple architectures are being trained; why not reuse the weights and just change the architecture? After all, it is the architecture that the search process aims to find and not the weights. In order to enable reusing weights the search space needs to be limited through a stricter structural definition.

Figure 3: NAS cell modeled as Directed Acyclic Graph where the edges considered operations and the nodes are computational units that transform and combine previous nodes to create new hidden states.

By defining the number of hidden states that are allowed to exist within the searched block, the search space becomes bound. In other words, the number of possible combinations of operations within the block is a large number but not infinite. If the hidden states are then ordered and their allowed topology predefined as a directed acyclic graph(DAG), the search space will look like in Figure 3. Using this search space the architectures suggested by the controller can be seen as sub-networks from a larger network, where the larger network and the sub-networks share the same hidden states (nodes). When the controller suggests a network architecture, it will mean that a subset of the connections (edges) will be selected and the hidden states (nodes) will be assigned new operations. This formulation means that it is easy to programmatically save the weights of operations on the nodes, which enables weight inheritance. In a NAS setting this means that the weights of the previous architecture can be used as an initialization for the next sampled network[6]. Initialization is known to work well independent of task or operations[7] and give the possibility for faster training as the models are not trained from scratch.

Now that training each model completely from scratch is no longer needed, the training and evaluation of networks is much faster. So fast in fact that it only takes 0.45 days on a single GPU, which is about 1000 times faster than previously[6]. The combination of the optimization techniques has resulted in an impressive speed up for reinforcement learning based NAS. The improvements have all been centered around evaluating individual architectures faster. However, reinforcement learning methods are not known to be the fastest at learning; in the goal of further improving NAS is there perhaps an alternative search process; that can traverse the search space in a more efficient manner? In the reinforcement learning based NAS process there are multiple models that are trained in order to find the best. Is there perhaps a way to avoid training all of these models and only train one model?

Differentiability

In the DAG formulation of the search space the networks trained are sub-networks of a larger network. Is it possible to train this larger network directly and somehow understand which operations are contributing the most? The answer is yes: it is possible!

Figure 4: a) Operations on the edges are initially unknown. b) Continuous relaxation of the search space by placing a mixture of candidate operations on each edge c) some weights increases and some falls during bilevel optimization d) final architecture is constructed only by taking edges with the maximum weight between two nodes[8].

If the controller is removed and the edges are changed to instead represent all possible operations, it is possible to differentiate the search space. In this dense architecture all the possible operations are combined in a weighted sum at every node. The weights of the summations are learnable parameters, which enables the network to scale the different operations. This means that operations that don’t help the performance can be scaled down and “good” operations can be scaled up. All one has to do after training the larger network is to observe the weights and pick the operations corresponding to the larger weights.

By differentiating the search space and training the larger network(commonly referred to as the “supernetwork”) there is no longer a need to train multiple architectures and one can use standard gradient descent optimizers. The differentiability of NAS opens up a plethora of possible next developments. One example of this is differentiable sampling in NAS[9], which pushes the search time to only four hours since fewer operations need to be used per forward pass and backpropagation in the search.

Some closing remarks

Here is where I’ll stop the story of how NAS was improved from many days to a few hours of training time. In this article I’ve tried to give an overview of the most important ideas that have brought us to where neural architecture search is today. Since NAS is now efficient enough for anyone with a GPU to use, I’ll take a deep dive into the most popular differentiable NAS technique called DARTS[8] in my next article. In this deep dive I’ll raise some questions about the algorithm and run experiments to try to evaluate them. Furthermore, I’ll present an attempt to find a more generalizable approach to differentiable NAS.