Dynamic Filter Networks

Dynamic Filter Networks

2019-06-10 11:29:19

Paper：http://papers.nips.cc/paper/6578-dynamic-filter-networks.pdf 

Code (Lasagne)：https://github.com/dbbert/dfn 

 

1. Background and Motivation:

标准卷积神经网络中，都是采用训练之后学习到的 filters，而本文则提出了一种新的学习框架，称为：Dynamic Filter Network，该网络中的 filter 是根据输入动态生成的。 这种框架更加灵活，强大，并没有提增加模型的参数个数。广泛的 filtering operation 都可以采用这种框架，包括：local spatial transformations, selective blurring 或者 adaptive feature extraction. 此外，也可以用于循环网络框架中（如 Recurrent architecture）。

 

该模型包含两个部分：

1). filter-generating network, 可以基于给定的输入，动态的生成 sample-specific filter network。该参数并非是固定的，像正则化模型参数；

2). dynamic filtering layer, 然后将这些 filters 应用到输入上。

这两个模块都是可微分的。作者还基于此提出了一种 dynamic local filtering layer，不但是 sample-specific，而且是 position-specific 的。这些 filters 从不同 position 以及 不同 samples 都是可变化的，允许我们在在输入上进行更多操作。该框架可以学习 spatial 和 photometric changes，因为像素不是简单的进行放置的，filters 可能在所有的近邻上进行操作。

 

2. Dynamic Filter Networks : 

 

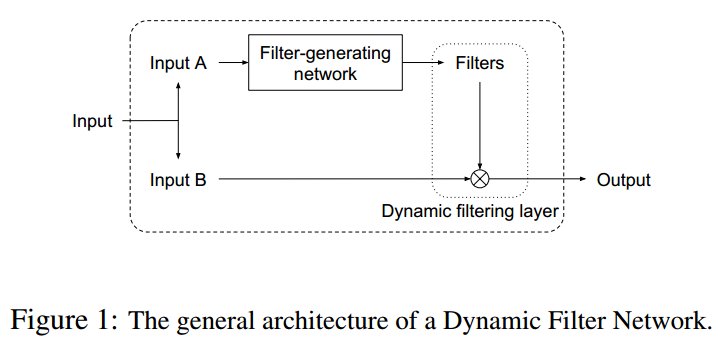
如上图所示，本文所提出的网络的结构，主要包含两个模块：一个是 filter 产生模块，另一个是 dynamic filter layer。这两个模块都是可微分的，模块的输入可以是相同的，也可以是不同的，具体跟所涉及的任务相关。为了清晰起见，作者这里解释了 model parameters 和 dynamically generated parameters 的区别：model parameters 表示预先进行初始化的 layer parameters，仅仅在 training 阶段进行更新；而 dynamic generated parameters 是 sample-specific 的，并且可以快速的进行产生，而不需要进行初始化。本文所涉及的 filter-generating network 输出的是 dynamically generated parameters，但是该网络本身的参数是属于 model parameters。

 

2.1 Filter-Generating Network: 

滤波产生网络的输入是 $I_A$, 其输出 filter $F_{\theta}$，该滤波器可以用于输入 $I_B$ 上来产生一个输出 G，滤波器的大小决定了感受野的大小，其选择依赖于具体应用。感受野的大小还可以通过堆叠多层动态滤波模块来实现增加。

 

2.2 Dynamic Filtering Layer :

该模块将输入的图像或者特征 $I_B$ 作为输入，然后输出滤波之后的结果 G。

Dynamic convolutional layers: 就前文讲的，此处的卷积操作用的卷积核是动态生成的，而不是预训练产生的。其公式化表达如下：

 

这些 filter 是 sample-specific 的，并且是基于 filter-generating network 的输入的。动态卷积层如下图所示：

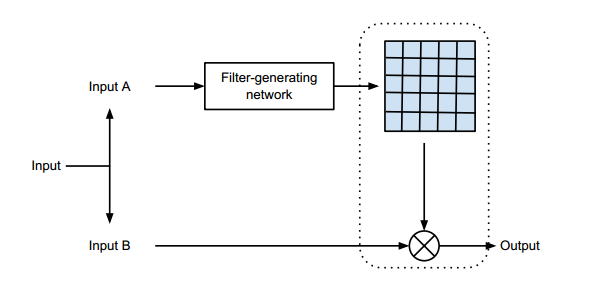
Dynamic local filtering layer : 

作为上述 dynamic convolution layer 的一种拓展，dynamic local filtering layer 提供了一种更有意思的结果。在该 layer 中，filter operation 不再是 translation invariant。不同的滤波器用于输入 $I_B$ 的不同位置，这一点与传统的局部连接 layer 类似：对于输入 $I_B$ 的每一个位置 (i, j)，一个特定的 local filter $F_{\theta}^{(i, j)}$ 是被用于 $I_B(i, j)$ 位置中心区域的：

 

用于这种 layer 的 filters 不再是 sample-specific，而是 position-specific。注意到，上述讲的 dynamic convolution 是 local dynamic filtering 的特例，其中 local filters 是在整个图像区域共享的。如下图所示，

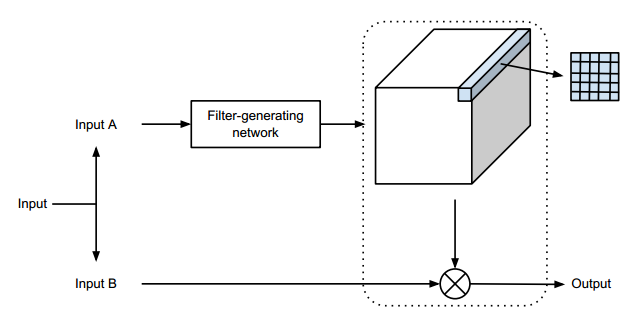
当输入 $I_A$ 和 $I_B$ 都是图像的时候，一个很自然的方法是用卷积网络来实现 filter-generating network。也就是说，所产生的 position-specific filters 是依赖于 $I_A$ 区域中的 local image regions 的。

 

  

==