Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

2019-05-20 19:34:55

Paper: https://arxiv.org/pdf/1902.09630.pdf 

Project page: https://giou.stanford.edu/ 

Code: https://github.com/generalized-iou 

 

1. Background and Motivation: 

IoU (Intersection over Union) 是物体检测领域最常用的评价指标，用于衡量任意两个形状之间的相似性。IoU 将物体的形状信息，如：width，height，and locations of two bounding boxes，编码为 region property，然后计算一个聚焦于该区域的度量。这个性质使得 IoU 对 scale 有不变性。由于具有这样的特点，IoU 被广泛的应用于物体检测，分割，跟踪等任务。

 

从上述内容可以发现，最小化常用的损失 与 改善他们的 IoU 值，之间并没有强烈的关系。如图 1（a）所示：（绿色的BBox 为真值，黑色的为预测的结果）

为了简化起见，我们假设两个 BBox 的一个角固定，所以，任何预测的 BBox，只要第二个角在圆周线上，将会产生相同的 l2-norm distance；然而，IoU值却明显的不同。可以发现，regression loss 的优化 和 IoU values 之间的 gap，并不能很简单的跨越。

 

本文针对该问题，探索了 IoU 的新的计算方法。作者这里借鉴了 UnitBox 的思想，直接将 BBox 作为优化目标进行回归。所以，将 IoU 作为 2D 物体检测任务的目标函数就更适合了。但是，IoU 作为 metric 和 loss 有如下的不足：如果两个物体根本没有重合，那么 IoU value 将会是 0，并且不会反应两个 BBox 到底有多远。在这种不重合的情况下，如果用了 IoU 作为损失函数，那么梯度将会为 0，无法进行优化。

 

在本文中，作者通过解决这个不重合的问题，克服了 IoU 的弱点。作者确保其拓展版本的有如下的特性：

a). 与 IoU 一样，拥有相同的定义，即：将对比物体的形状属性编码为区域属性（region property）；

b). 保持了 IoU 的尺寸不变性；

c). 确保了在重合物体上与 IoU 的强烈相关性；

我们引入该 generalized verison of IoU, named GIoU, 作为一种新的对比方式。也提供了一种分析性的方案，来计算 GIoU，允许其作为 loss function。将 GIoU loss 引入到顶尖的物体检测算法中，我们的方法稳定的提升了其在主流物体检测benchmark 上检测性能。

 

2. Generalized Intersection over Union : 

常规的 IoU 的定义如下：

 

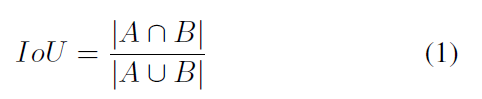
IoU 有如下的两个优势：

1). IoU 作为距离，可以看做是一种 metric；

2). IoU 对问题的尺寸具有不变性（Invariant to the scale of the problem）；

与此同时，也有如下的一个劣势：如果两个 BBox 不重合，那么其 IoU 得分就是 0。那么，此时的 IoU 无法反映出两个BBox 真实的距离。

 

作者提出的 GIoU 可以很好的解决这个问题，具体的计算方式如下：

 

首先，计算两个 BBox  A 和 B 的 smallest convex shapes C, 同时包含 A and B; 

然后，我们计算如下的比值：分子是 排除 A 和 B 后的 C的区域，分母是 C 的总面积；这个表达了 A 和 B 之间的空闲区域的大小比例；

最终，将 IoU 的值，减去上述的比值，就可以得到 GIoU 的值。 

 

上图中的绿色区域，即展示了所要计算的区域 C 的面积。

 

3. Experiments：

 

==== Core Code: 

def bbox_transform(deltas, weights):
    wx, wy, ww, wh = weights
    dx = deltas[:, 0::4] / wx
    dy = deltas[:, 1::4] / wy
    dw = deltas[:, 2::4] / ww
    dh = deltas[:, 3::4] / wh

    dw = torch.clamp(dw, max=cfg.BBOX_XFORM_CLIP)
    dh = torch.clamp(dh, max=cfg.BBOX_XFORM_CLIP)

    pred_ctr_x = dx
    pred_ctr_y = dy
    pred_w = torch.exp(dw)
    pred_h = torch.exp(dh)

    x1 = pred_ctr_x - 0.5 * pred_w
    y1 = pred_ctr_y - 0.5 * pred_h
    x2 = pred_ctr_x + 0.5 * pred_w
    y2 = pred_ctr_y + 0.5 * pred_h

    return x1.view(-1), y1.view(-1), x2.view(-1), y2.view(-1)


def compute_iou(output, target, bbox_inside_weights, bbox_outside_weights, transform_weights=None, batch_size=None):
　　 ## the output is predicted bounding box, the target is ground truth bbox. (you need to transform them into tensor, when use this function)
    if transform_weights is None:
        transform_weights = (1., 1., 1., 1.)

    if batch_size is None:
        batch_size = output.size(0)

    x1, y1, x2, y2 = bbox_transform(output, transform_weights)
    x1g, y1g, x2g, y2g = bbox_transform(target, transform_weights)

    x2 = torch.max(x1, x2)
    y2 = torch.max(y1, y2)

    xkis1 = torch.max(x1, x1g)
    ykis1 = torch.max(y1, y1g)
    xkis2 = torch.min(x2, x2g)
    ykis2 = torch.min(y2, y2g)

    xc1 = torch.min(x1, x1g)
    yc1 = torch.min(y1, y1g)
    xc2 = torch.max(x2, x2g)
    yc2 = torch.max(y2, y2g)

    intsctk = torch.zeros(x1.size()).to(output)
    mask = (ykis2 > ykis1) * (xkis2 > xkis1)
    intsctk[mask] = (xkis2[mask] - xkis1[mask]) * (ykis2[mask] - ykis1[mask])
    unionk = (x2 - x1) * (y2 - y1) + (x2g - x1g) * (y2g - y1g) - intsctk + 1e-7
    iouk = intsctk / unionk

    area_c = (xc2 - xc1) * (yc2 - yc1) + 1e-7
    miouk = iouk - ((area_c - unionk) / area_c)
    iou_weights = bbox_inside_weights.view(-1, 4).mean(1) * bbox_outside_weights.view(-1, 4).mean(1)
    iouk = ((1 - iouk) * iou_weights).sum(0) / batch_size
    miouk = ((1 - miouk) * iou_weights).sum(0) / batch_size

    return iouk, miouk   ## the iouk is regular IoU value, the miouk is the GIoU value.