End-To-End Memory Networks
End-To-End Memory Networks
2019-05-20 14:37:35
Paper：https://papers.nips.cc/paper/5846-end-to-end-memory-networks.pdf
Code：https://github.com/facebook/MemNN
1. Background and Motivation:
现在人工智能研究的两个挑战性的问题是：第一是能够构建模型，使其能够进行多个计算步骤，以服务于回答问题或者完成一个任务；另一个是可以建模时序数据中的长期依赖关系。最近，基于存储和 attention 机制的模型开始复兴，而构建这种存储对解决上述两个问题，提供了可能的方向。在前人的工作中，存储是建立在连续的表达上；从该存储中进行读取和写入的操作，以及一些其他的操作步骤，都通过神经网络的动作来建模。
在本文中，作者提出了一种新颖的 RNN 结构，其能够循环的从一个可能的大型额外记忆单元中多次进行读取，然后输出一个符号。我们的模型可以看做是连续的 Memory Network。我们的模型也可以看做是一种 RNNsearch 的版本，每输出一个符号都带有多个 hops。 我们的实验证明，长期记忆的 the multiple hops 对取得较好的效果，具有关键性的作用。训练这些记忆表达，可以以一种 end-to-end manner 来将其接入到我们的模型中。
2. Approach:
我们的模型将离散元素集合 x1, x2, .... xn（存储在 memory 中）和 query q 作为输入，然后输出一个 answer a。每一个 xi，q，a 都包含从字典中得到的符号表达。模型将所有的 x 写入到 memory，直至达到一个固定的 buffer size，然后为 x 和 q 找到一个连续的表达。这个连续的表达然后通过 multiple hops 来进行处理，输出 a。这就允许误差信号可以沿着多次记忆的访问进行传播，在训练过程中传递到输入。
2.1 Single Layer：
Input memory representation:
假设我们给定了一个输入集合 x1, x2, ... , xi 并且存储在记忆单元中。整个 {xi} 的集合可以转换为 memory vector {mi}，通过将每一个 xi 映射到连续的空间，最简单的情况就是，利用 an embedding matrix A。Query q 然后也被映射，得到一个中间状态 u。在 embedding space 中，我们通过采用内积，然后用 softmax 函数，计算 u 和 每一个 memory mi 之间的匹配：
通过这种方式定义的 p，是基于输入的概率向量。
Output memory representation :
每一个 xi 都有一个对应的输出向量 ci（通过另一个 embedding matrix C 来进行转换）。从记忆 o 中得到的响应，用概率向量 p 和 转换输入 ci 之间的加权求和：
因为从输入到输出的函数是平滑的，我们可以简单的计算其梯度，然后进行反传即可。其他最新提出的一些 memory 和 attention 的方法，也是采用这种方法。
Generating the final prediction :
在单个 layer 的情况下，输出向量 o 的和，以及 输入映射 u 都被用一个权重矩阵 W 进行传递，然后用 softmax 得到其预测的 label：
总体的模型如图 1 （a）所示。
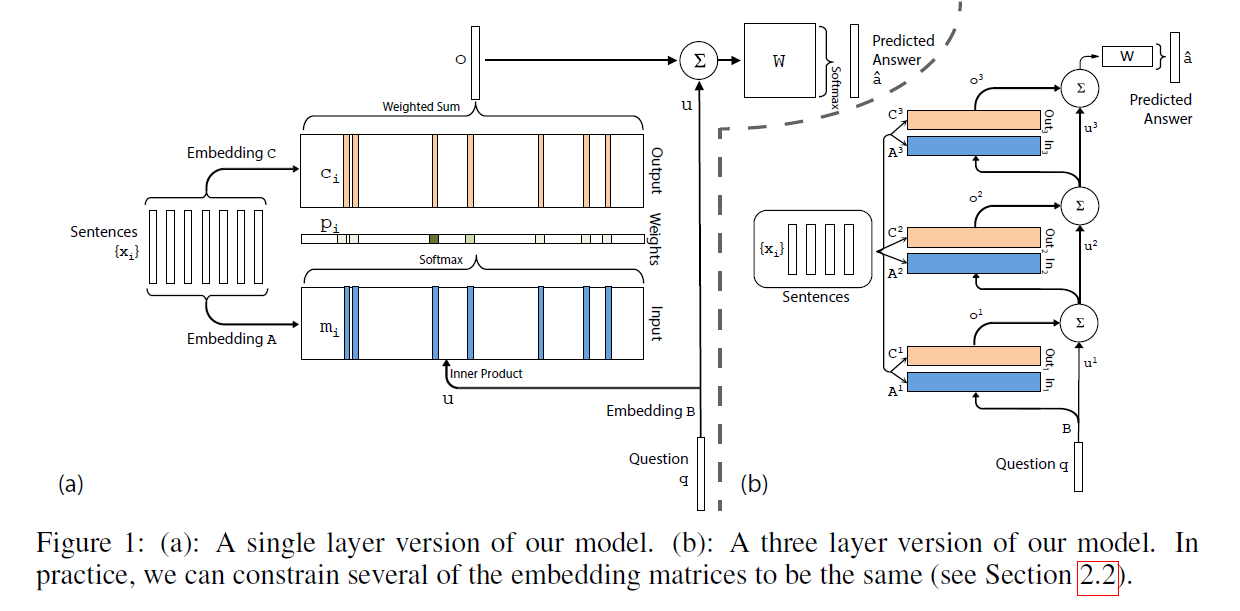
2.2 Multiple Layers:
我们现在将模型拓展为可以处理 K hop operations 的情况。这些 memory layers 可以通过如下的方式进行堆叠：
1). 第一层上面的那些 layers 的输入是：来自 layer k 的输出 $o^k$ 以及输入 $u^k$ 的和：
$u^{k+1} = u^k + o^k$.
2). 每一层都有其各自的 embedding matrices $A^k, C^k$，用于映射其输入 $x_i$。
3). 在网络的顶端，W 的输入也考虑了 the top memory layer 的输入和输出：
$\hat{a} = Softmax(W u^{K+1}) = Softmax(W (o^K + u^K))$。
作者在这个模型中，考虑了如下两种加权的方式：
1. Adjacent：某一层的输出是上一层的输入，即： $A^{k+1} = C^{k}$。我们也给定了如下的约束：a). 答案预测矩阵 要和 最终输出的映射相同，即：$W^T = C^K$， b). question embedding 要和 第一层的 input embedding 保持一致，即：$B = A^1$。
2. Layer-wise (RNN-like): 输入和输出 embedding 在不同layers 之间是相同的，即：$A^1 = A^2 = ... = A^K$ and $C^1 = C^2 = ... = C^K$。我们已经发现，在 hops 之间用一个线性映射 H 来更新 u 是有效的；即，$u^{k+1} = H u^{k} + o^k$。这个映射是沿着剩下的参数学习的。
==
