论文笔记：Auto-DeepLab: Hierarchical Neural Architecture Search for Semantic Image Segmentation

Auto-DeepLab: Hierarchical Neural Architecture Search for Semantic Image Segmentation
2019-03-18 14:45:44

 

Paper：https://arxiv.org/pdf/1901.02985 

Offical TensorFlow Code: https://github.com/tensorflow/models/blob/master/research/deeplab/core/nas_network.py 

PyTorch Code: https://github.com/Dawars/auto_deeplab-pytorch 

Video Tutorial (韩语): https://www.youtube.com/watch?v=ltlhQXHGzgE 

作者主页（Liang-Chieh Chen）：http://liangchiehchen.com/ 

 

另外一个关于 NAS 做语义分割的工作是：Nekrasov, Vladimir, Hao Chen, Chunhua Shen, and Ian Reid. "Fast Neural Architecture Search of Compact Semantic Segmentation Models via Auxiliary Cells." arXiv preprint arXiv:1810.10804 (2018). 

 

本文首次将 Neural Architecture Search（NAS） 引入到 semantic segmentation 领域，自动搜索网络结果，用于语义分割。

 

3. Architecture  Search Space：

本节描述了我们的双层等级结构搜索空间。对于 inner cell level，我们重新利用了前人的工作，保持一致。对于 outer network level，在对许多工作进行总结和观察之后，作者提出一种新的搜索空间。

3.1 Cell Level Search Space：

作者定义 cell 为一个小的全卷机模块，通常重复很多次，以形成整个的神经网络。具体来说，一个 cell 是一个 directed acyclic graph，包含 B 个 blocks。

每个 block 是一个 two-branch structure，将 2 个输入tensors 映射为 1 个输出 tensor。在 cell l 中的 Block i 可能是由 五元组指定的（I1, I2, O1, O2, C），其中 I1，I2 是输入 tensor 的选择，O1，O2 是 layer types 的选择，C 是用于组合 the two branches 的单独输出，以构成该 block 的输出 tensor，$H_i^l$。该 cell 的输出 tensor $H^l$ 仅仅是该模块输出 tensors 的简单组合{$H_1^l, ... , H_B^l$}。

 

可能的输入 tensors $I_i^l$ 的集合，包含前一个 cell $H^{l-1}$ 的输出，前前个 cell $H^{l-2}$，以及前一个 block 在当前 cell {H_1^l, ... , H_i^l} 的输出。所以，我们在一个 cell 中，添加越多的 blocks，下一个 block 就可能会有更多的输入来源。

 

可能的 layer types，O，包含下列 8 个操作符，都与当前的 CNNs 紧密相关：

 对于可能的组合操作函数，C，作者这里仅采用 element-wise addition。

 

3.2　Network Level Search Space：

在图像分类的 NAS framework 中，一旦一个 cell structure 被发现，整个的网络结构是用预先定义的模型来得到的。所以，the network-level 不是结构搜索的一部分，所以，其搜索空间从未被探索过。

这种预先定义的模式是非常简答和直观的：一些 “Normal cells”  （Cells that keep the spatial resolution of the feature tensor）通过添加 “reduction cells” （cells that divide the spatial resolution by 2 and multiply the number of filters by 2） 被单独的分离。这种保持 downsampling 的策略，在图像分类的任务上是合理的。但是，在 dense image prediction 中，保持高分辨率同样重要，从而导致了更多的网络层次。

 

在进行 dense image prediction 的众多网络结构中，我们注意到如下两个原则是一致的：

1. the spatial resolution of the next layer is either twice as large, or twoice as small, or remains the same; (下一层的分辨率要么是 两倍大，两倍小，或者保持不变)

2. the smallest spatial resolution is downsampled by 32. （最小的空间分辨率下降为32）

 

服从这些公共的准则，我们提出如下的网络级别的搜索空间。网络的开始是一个 two-layer “stem” structure，每一次以幅度 2 来降低空间分辨率。在那之后，总共有 L layers 未知的空间分辨率，最大下降幅度为 4，最小的分辨率被下采样了 32. 由于每一层在空间分辨率上最多两个不同，在 stem 之后的第一层可以被将分辨率 4 或者 8. 我们在图 1中，展示了我们的网络级别搜索空间。我们的目标是在这 L层路径上，找到一个较好的 path。

 

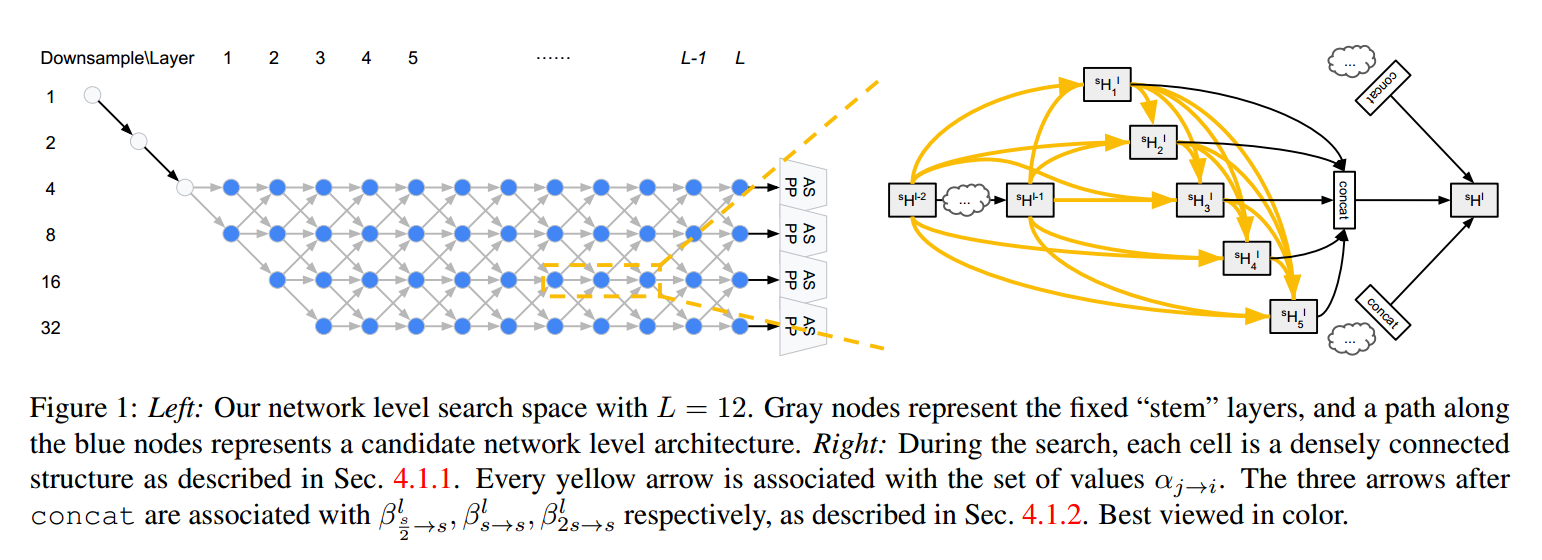
在图 2 中，我们表明：作者所提出的 search space 是一种 general 的方法，足够 cover 到很多流行的网络设计。在未来工作中，作者打算将该搜索空间，拓展到甚至包含 U-Net 结构。

由于本文既考虑了 cell level architecture ，又考虑到了 cell level architecture，所以，我们的搜索任务，相对于前人的工作，则更加具有挑战性以及 general。

 

 

4. Methods：

我们首先介绍 a continuous relaxation of the discrete architecture，然后介绍如何如何通过优化来实现结构化搜索，然后是在搜索结束后，如何编码回一个离散的结构。

4.1 Continuous Relaxation of Architecture：

4.1.1 Cell Architecture：

作者采用前人提出的连续松弛，每一个 block 的输出向量是和所有的 hidden states 相连的：

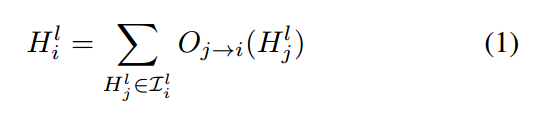
此外，我们用其连续的松弛 $\hat{O_{j->i}}$ 来估计每一个 $O_{j->i}$ ，其定义如下：

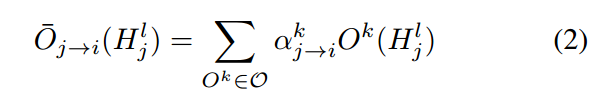
其中，

另外，是 normalized scalars associated with each operator, 用 softmax 函数可以很容易的实现。

 

回顾 3.1 小节，我们得到 cell level update 的方式：

 

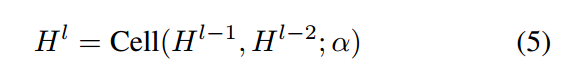
4.2 Network Archtiecture: 

在一个 cell 中，所有的 tensor 都拥有相同的 spatial size，以确保公式（1， 2）中加权求和。然而，就像图 1所示，tensors 可能在 network level 包含不同的 size，所以，为了设置连续的松弛，每一个 layer l 将会最多包含四个 hidden states，上标符号表示 spatial resolution。

 

我们设计 network level 连续松弛，以准确的匹配搜索空间。我们给图 1 的每一个灰色的箭头加一个 scalar，于是，network level 的 update 可以定义为：

其中，s = 4, 8, 16, 32 and l = 1,2, ... , L. 参数 $\beta$ 归一下如下：

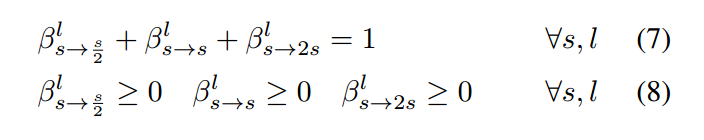
也是用 softmax 的方式进行。

 

公式（6）表明如何将 two-level hierarchical 的连续松弛进行集合。特别的，$\beta$ 控制着 the outer network level，所以，依赖于空间尺寸和 layer index。$\beta$ 的每个 scalar 都控制了一个完整的 $\alpha$ 集合，然而 $\alpha$ 指定了 the same architecure that depends on neither spatial size nor layer index。

 

如图 1 所示，ASPP （Astrous Spatial Pyramid Pooling）modules 对 第 L-th layer 的每一个空间分辨率的都链接了（atrous rates 可以调整）。他们的输出，在 sum 之前，是 bilinear upsample 到原始的分辨率，以产生预测。

 

4.2 Optimization：

将该连续的松弛引入进来的优势是：这些 scalar 控制了不同隐层状态的链接强度（controlling the connection stength between different hidden states），are now part of the differentiable computation graph. 所以，这可以通过 gradient descent 的方法来进行有效的优化。作者采用 first-order approximation，将训练数据分为两个集合 trainA 和 trainB。其依次优化过程如下：

 

其中，损失函数 L 是依赖于语义分割的交叉熵。

 

4.3 Decoding Discrete Architecture: 

Cell Architecture: 作者解码该离散 cell architecture，首先，对每一个 block，保持 2 个最强的 predecessors，然后，通过 argmax 来选择最像的操作符。

Network Architecture：公式（7）表明：the "outgoing probability" at each of the blue nodes in Fig. 1 sums to 1. 实际上，$\beta$ 值可以表示为：沿着不同“时间步骤（layer number）”，不同“state”（Spatial resolution）之间的转移概率（“transition probability”）。直观的来说，我们的目标是：从头到尾，找到一个 path，使其获得最大化的概率（maximum probability）。该路径可以有效的通过 the classic Viterbi algorithm，来进行解码。

 

 

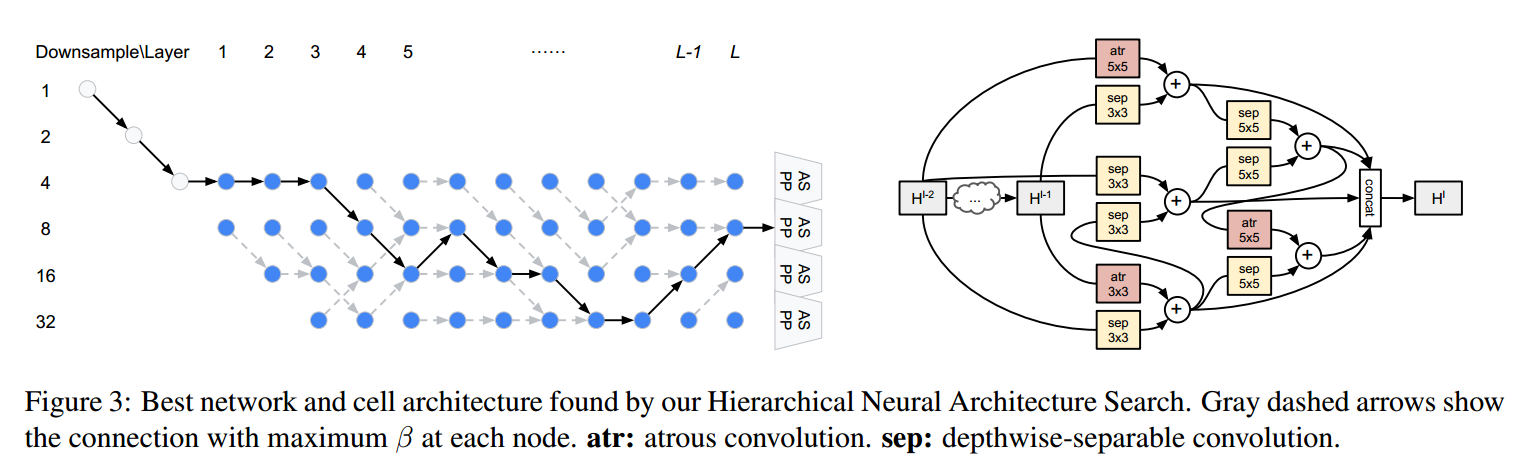
5. Experimental Results:  

在本节中，作者首先介绍了接收搜索的具体实现细节，以及搜索的结果。然后，介绍了语义分割在多个benchmark 数据集上的结果。

5.1 Architecture Search Implementation Details：

作者考虑到 12 层的网络，并且设置一个 cell 中的 B = 5 blocks，该 network level search space 有 $2.9*10^4$ 个独特的 path，cell structure 的个数为 $5.6*10^{14}$。所以，联合的，等级搜索空间的大小为 $10^{19}$。

 

作者采用常用的套路，即：double the number of filters，当降低 feature tensor 的  width 和 height 时。图1中的每个绿色节点，都有 downsample rate s，拥有 B*F*s output filters，其中，F 是 filter multiplier 控制着模型的容量。在结构搜索的过程中，我们设置 F = 8。stride 为 2 的 convolution 被用于所有的 s/2 到 s 的连接，都用于降低分辨率大小 和 增加滤波器的个数。在 1*1 的卷积后，用 bilinear upsampling 来用于 2s -> s 的链接，都用于增加分辨率 和 降低滤波器的个数。

 

ASPP module 拥有 5 个分支：one 1*1 convolution, three 3*3 convolution （不同的空洞率），以及 pooled image feature. 在搜索的过程中，我们简化 ASPP 使其拥有 3 branches，通过仅适用一个 3*3 convolution （空洞率为 96/s）。每个 ASPP 分支产生的滤波器的个数为 B*F*s。

 

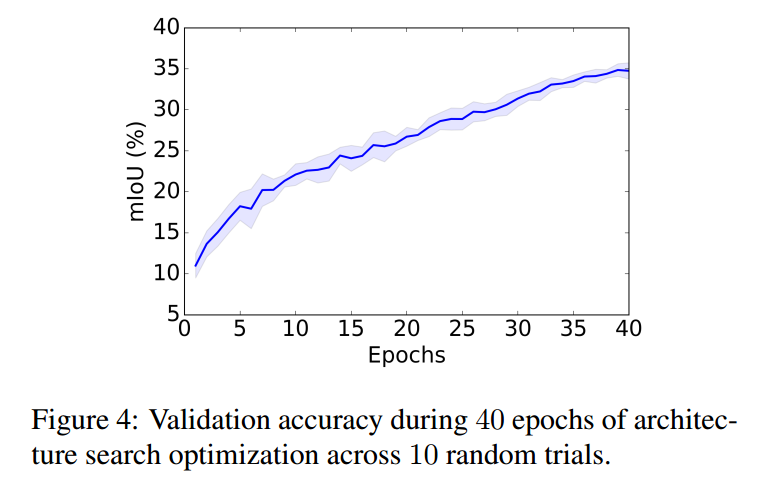
我们在 Cityscapes dataset 上进行网络结构的搜索进行语义分割。具体来说，作者随机的从 512*1024 的图像上裁剪出 321*312 的图像。然后随机的从 train_fine 中选择一般图像放到 trainA 中，剩下的一般作为 trainB。本文的一个亮点是：整个网络结构的搜索过程仅仅在 P100 GPU 上搜索一天就完成了。作者尝试了优化更多的时间，但是并未见到效果有显著的提升。图4，展示了 验证集精度的稳定变化曲线。

 

5.2 语义分割结果：

 

==
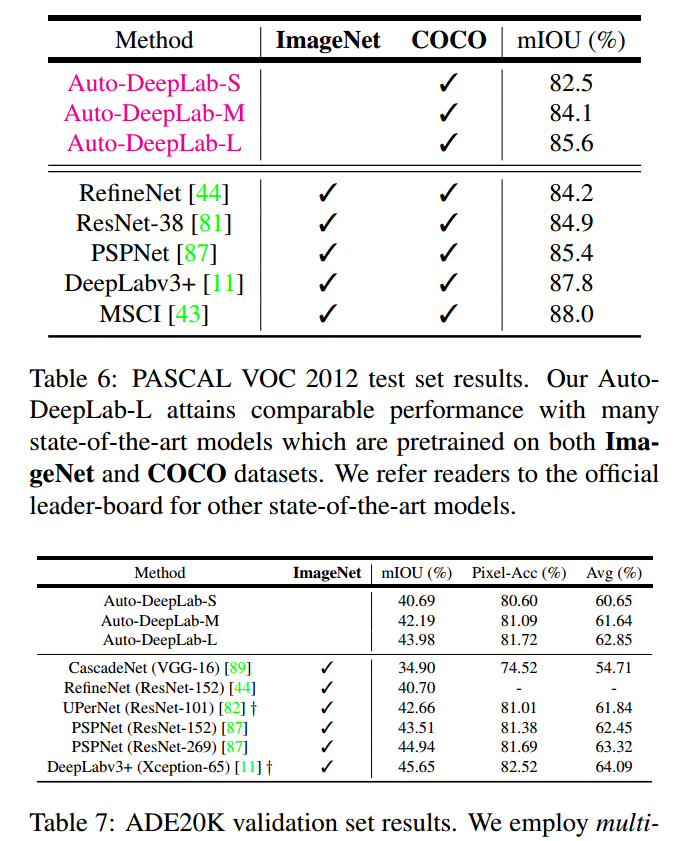