Pytorch_2.3_自动求梯度
2.3 自动求梯度
2.3.1 属性跟踪
Tensor 中的属性.requires_grad 是用来跟踪所有操作的,深一步的作用是用来进行梯度传播,目前可以将其理解为操作的跟踪,即对Tensor进行的操作进行描述。
需要创建一个Tensor并将其requires_grad = True
import torch
x = torch.ones(2,2,requires_grad = True)
print(x)
print(x.grad_fn)
# .grad_fn 用来显示操作的类型
# 此时 x 刚被创建 所以操作类型为 None
tensor([[1., 1.],
[1., 1.]], requires_grad=True)
None
y = x + 2
print(y)
print(y.grad_fn)
tensor([[3., 3.],
[3., 3.]], grad_fn=<AddBackward0>)
<AddBackward0 object at 0x0000022A5C33F198>
y 是通过x创建的 所以y的操作类型显示的是加法操作 AddBackward0
直接创建的x 成为叶子节点,叶子结点对应的grad_fn 是 None
z = y * y * 3
out = z.mean()
print(z)
print(out)
tensor([[27., 27.],
[27., 27.]], grad_fn=<MulBackward0>)
tensor(27., grad_fn=<MeanBackward0>)
可以通过.requires_grad_() 来改变 requires_grad的属性
a = torch.randn(2,2)
a = a * 5
print(a)
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)
tensor([[ 6.1521, -4.8040],
[-0.3007, 6.0043]])
False
True
<SumBackward0 object at 0x0000022A5C04E828>
2.3.2 梯度
print(out)
tensor(27., grad_fn=<MeanBackward0>)
out.backward() # .backward() 只能在第一次运行 之后运行必须重新运行前面的步骤
print(x.grad)
tensor([[4.5000, 4.5000],
[4.5000, 4.5000]])
这里的梯度计算就是求out 对x 的偏导
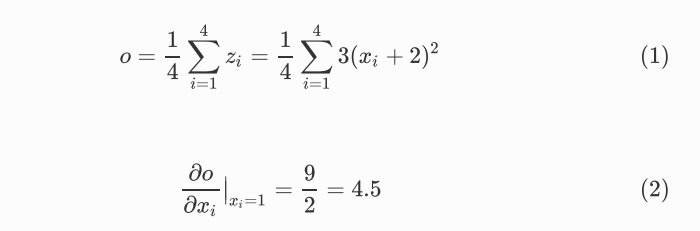
grad反向传播过程中是累加的,所以每次方向传播前需要将梯度清零 .grad.data.zero_()
out2 = x.sum()
out2.backward()
print(x.grad)
out3 = x.sum()
x.grad.data.zero_() # 将之前的梯度清零
out3.backward()
print(x.grad)
tensor([[5.5000, 5.5000],
[5.5000, 5.5000]])
tensor([[1., 1.],
[1., 1.]])
目前只允许标量对张量求导,求导结果是和自变量相同的张量
如果是对张量求导,则需要引入一个相同张量加权成标量
具体操作如下例
x = torch.tensor([1.0,2.0,3.0,4.0], requires_grad = True)
y = 2 * x
z = y.view(2,2)
print(z)
tensor([[2., 4.],
[6., 8.]], grad_fn=<ViewBackward>)
可以看出 z 不是一个标量,所以在调用backward时需要传入一个和z相同的权重向量进行加权求和得到一个标量
v = torch.tensor([[1.0,0.1],[0.01,0.001]],dtype = torch.float)
z.backward(v)
print(x.grad)
tensor([2.0000, 0.2000, 0.0200, 0.0020])
这里的z.backward(v)计算过程如下,摘自原文

如何中断梯度追踪
在计算过程中执行torch.no_grad(): 下的计算不会被追踪,求导时也不会被记录
x = torch.tensor(1.0,requires_grad = True)
y1 = x ** 2
with torch.no_grad():
y2 = x ** 3
y3 = y1 + y2
print(x.requires_grad)
print(y1, y1.requires_grad)
print(y2, y2.requires_grad)
print(y3, y3.requires_grad)
True
tensor(1., grad_fn=<PowBackward0>) True
tensor(1.) False
tensor(2., grad_fn=<AddBackward0>) True
可以看出 y2 的计算没有被跟踪
y3.backward()
print(x.grad)
tensor(2.)
如何修改Tensor 的值 而不影响反向传播 即梯度计算 可以利用Tensor.data
x = torch.ones(1,requires_grad = True)
print(x.data)
print(x.data.requires_grad)
y = x * 2
x.data *= 100
y.backward()
print(x)
print(x.grad)
#
tensor([1.])
False
tensor([100.], requires_grad=True)
tensor([2.])
【总结】
- 如何跟踪计算过程的属性 requires_grad = True
- 梯度是如何计算的 .backward() 就是求偏导数
- 标量对张量求导 张量对张量求导
- 中断梯度跟踪 torch.no_grad()
- 改变tensor 不改变梯度 .data
posted on 2020-02-01 22:55 wangxiaobei2019 阅读(239) 评论(0) 编辑 收藏 举报





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· 字符编码:从基础到乱码解决
· SpringCloud带你走进微服务的世界