最长公共子序列及其引申问题

最长公共子序列是经典的动态规划问题，在很多书籍和文章中都有介绍，这里对这一经典算法进行回顾并对两个follow up questions进行总结和分析。

1. 回顾LCS（longest common subsequence）解法，求LCS长度

典型的双序列动态规划问题，dp[i][j]表示第一个序列前i项与第二个序列的前j项....

所以对应此题，dp[i][j]表示序列s1的前i项与序列s2的前j项的最长公共子序列。

得到如下递推关系式：

dp[i][j] = dp[i - 1][j - 1] + 1                  if s1[i - 1] == s2[j - 1]

　　　　= max(dp[i - 1][j], dp[i][j - 1])   if s1[i - 1] != s2[j - 1] ;

对dp[0][j] j = 0,1,... 于 dp[i][0] i = 0,1...初始化，根据递推关系式则可以得到结果。

程序：

int longsetCommonSubsequence(const string& s1, const string& s2) {
    int sz1 = s1.size(), sz2 = s2.size();
    int dp[sz1 + 1][sz2 + 1];
    for (int i = 0; i <= sz1; ++i) {
        dp[i][0] = 0;
    }
    for (int i = 0; i <= sz2; ++i) {
        dp[0][i] = 0;
    }
    for (int i = 1; i <= sz1; ++i) {
        for (int j = 1; j <= sz2; ++j) {
            if (s1[i] == s2[j]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[sz1][sz2];
}

 

2. 如何得到最长公共子序列？

其实本质上，当有了dp数组时，即得到了行程LCS的所有信息。

我们考察一个例子，求s1 = "ABCBDAB" 和 s2 = "BDCABA"的 LCS， 得到其dp数组如下。（图片来自邹博）

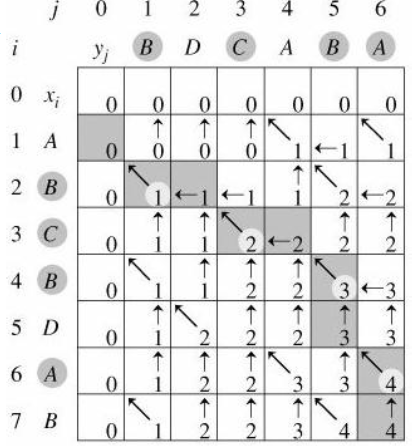
我们可以看到，当dp数组被填充完毕后。反向探索LCS的形成过程，结合递推公式可知，每一个添加到LCS中的字符是在s1[i - 1] == s2[j - 1]的情况下加入的。

也就是上述图中向同时向左上方的那些步骤，而对应s1[i - 1] != s2[j - 1]的那些步骤，则选择其dp值大的（原因在于生成的时候路径就是选的max）进行前进即可。

所以总结寻找LCS的算法步骤即：

如果s1[i - 1] == s2[j - 1]，将其push_back到结果中；

如果s1[i - 1] != s2[j - 1]，选择dp[i - 1][j]与dp[i][j - 1]中大的更新i--或j--。

直到i或者j达到0后，翻转上述结果即可。

代码：

string longsetCommonSubsequence2(const string& s1, const string& s2) {
    int sz1 = s1.size(), sz2 = s2.size();
    int dp[sz1 + 1][sz2 + 1];
    for (int i = 0; i <= sz1; ++i) {
        dp[i][0] = 0;
    }
    for (int i = 0; i <= sz2; ++i) {
        dp[0][i] = 0;
    }
    for (int i = 1; i <= sz1; ++i) {
        for (int j = 1; j <= sz2; ++j) {
            if (s1[i - 1] == s2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    string result;
    int i = sz1, j = sz2;
    while (i > 0 && j > 0) {
        if (s1[i - 1] == s2[j - 1]) { //对应的是s1[i - 1]， s2[j - 1]
            result.push_back(s1[i - 1]);
            i--;
            j--;
        }
        else {
            if (dp[i - 1][j] > dp[i][j - 1]) {
                i--;
            }
            else {
                j--;
            }
        }
    }
    reverse(result.begin(), result.end());
    return result;
}

 

3. 有多组解都要输出怎么办？

首先考虑什么时候会有多组解？还考虑上述图示可以发现，当s1[i - 1] != s2[j -1]但 dp[i - 1][j] == dp[i][j - 1]时，i--， j--均可。所以可能产生多组解。

想要输出所有解的想法其实也很直观，就是DFS，把所有情况都遍历一遍，并进行去重(代码中find语句)，把不同路径的相同解删除掉，即可得到所有解。

一段完整的，带简单测试的程序如下：

#include <iostream>
#include <string>
#include <vector> 
#include <algorithm>
using namespace std;
vector<int> temp;
vector<vector<int>> resultIndex;
void dfs(const vector<vector<int>>& dp, const string& s1, const string& s2, int i, int j) {
    if (i == 0 || j == 0) {
        if (find(resultIndex.begin(), resultIndex.end(), temp) == resultIndex.end()) {
            resultIndex.push_back(temp);
        }
        return ;
    }
    if (s1[i - 1] == s2[j - 1]) {
        temp.push_back(i - 1);
        dfs(dp, s1, s2, i - 1, j - 1);
    }
    else {
        if (dp[i - 1][j] > dp[i][j - 1]) {
            dfs(dp,s1,s2,i - 1, j);
        }
        else if (dp[i - 1][j] < dp[i][j - 1]) {
            dfs(dp, s1, s2, i, j - 1);
        }
        else {
            vector<int> temp2 = temp;
            dfs(dp,s1,s2,i - 1, j);
            temp = temp2;
            dfs(dp,s1,s2,i, j - 1);
        }
    }
    return;
}

vector<string> longsetCommonSubsequence2(const string& s1, const string& s2) {
    int sz1 = s1.size(), sz2 = s2.size();
    vector<vector<int>> dp(sz1 + 1,vector<int>(sz2 + 1));
    for (int i = 0; i < sz1; ++i) {
        dp[i][0] = 0;
    }
    for (int i = 0; i < sz2; ++i) {
        dp[0][i] = 0;
    }
    for (int i = 1; i <= sz1; ++i) {
        for (int j = 1; j <= sz2; ++j) {
            if (s1[i - 1] == s2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    vector<string> result;
    dfs(dp,s1,s2,sz1,sz2);
    for (int i = 0; i < resultIndex.size(); ++i) {
        string s;
        result.push_back(s);
        for (int j = resultIndex[i].size() - 1; j >= 0; --j) {
            result[i].push_back(s1[resultIndex[i][j]]);
        }
    }
    return result;

}

int main() {
    string s1 = "ABCBDAB", s2 = "BDCABA";
    vector<string> result = longsetCommonSubsequence2(s1,s2);
    for (int i = 0; i < result.size(); ++i) {
        cout << result[i] << endl;
    }
    return 0;
}