第一周：时间复杂度该怎么看？

文章小结

写在最前面，本文主要介绍了如何能快速判断代码段的时间复杂度（记忆模版），如果您寻找的并非此类文章则不必继续阅读后文。

1.算法时间复杂度是什么

 官方定义：算法在编写成可执行程序后，运行时所需要的时间资源。

 解读：可执行程序运行所需要时间的一个量化指标。例如O(1)，常量级。

2. 常见的时间复杂度

• O(1) ：常量级
• O(n)：线性
• O(logn)：对数
• O(nlogn)
• O(n^2)：平方
• O(k^n)：指数级
• O(n!)：阶乘级别

3.如何判断代码的算法时间复杂度

首先我们假设执行一行代码需要的时间为1， 判断代码时间复杂度就是是看算法执行次数和n的关系。

例如：下面代码的时间复杂度为O(1)

String dogName = "小黄";
Systerm.out.print("this is a dog " + dogName);

 

例2: 下面代码片段中，代码执行次数为n，代码时间复杂度为O(n)。

for (int i=0; i<n; i++) {
    Systerm.out.print("get num " + i);
}

 

4.如何快速判断代码时间复杂度。

想要快速判断代码片段时间复杂度有两个方法，记忆和公式。这里我们仅讨论记忆，记住代表性的模板就可以快速判断时间复杂度

// 时间复杂度：O(1)
int a = 1;
int b = 2;
Systerm.out.print("sum is" + (a+b));

// 时间复杂度：O(n)
for (int i=0; i<n; i++) {
    Systerm.out.print("get num " + i);
}

// 时间复杂度：O(n^2)
for (int j=0; j<n; i++) {
     for (int i=0; i<n; i++) {
       Systerm.out.print("get num " + (i+ j));
   }
}
// 时间复杂度：O(logn)
for (int i=0; i<n; i=i*2) {
    Systerm.out.print("get num" + i);
}

// 时间复杂度：O(2^n)
int fib(int n) {
　　if (n<=2) return n; 
　　return fib(n-1) + fib(n-2);
}

O(1)、O(n)、O(n^2) 相对比较容易理解，这里不在赘述。

分析下O(logn)是怎么得到的。
2^0 = 1
2^1 = 2
2^2 = 4
.....
2^k = n;  所以需要执行k次。k=log2n，系数可以忽略所以时间复杂度为 O(logn)。

 

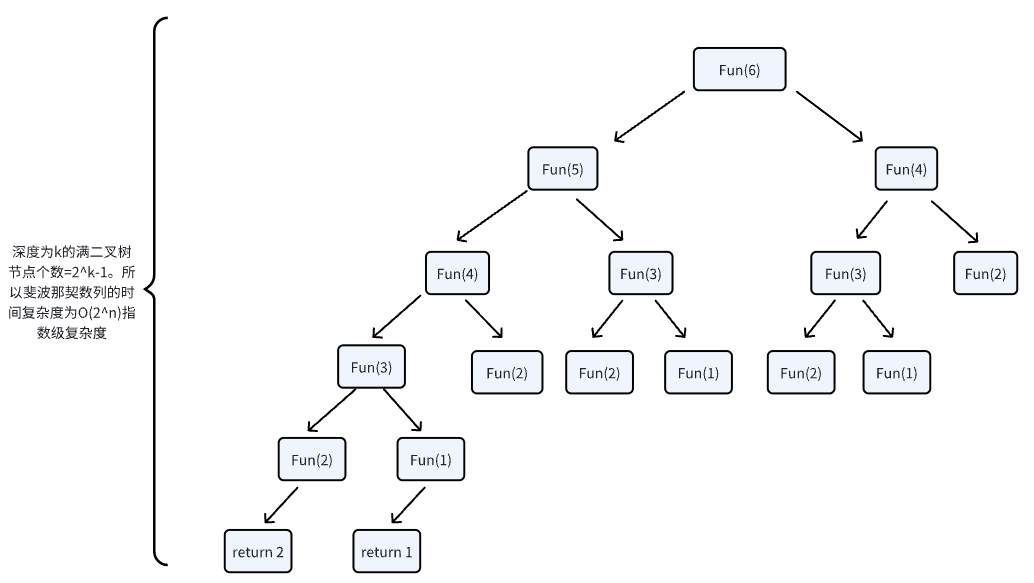
通过图例解释下O(k^n)指数级算法复杂度。以n=6为例，分析Fun(6)的计算逻辑，依据Fun(n) = Fun(n-1) + Fun(n-2)，做如下图的拆解。

 

 

 

5.延展内容。如何刷题（LeetCode）

区分业余和职业的最大区别在于是否有专项联系。比如乒乓球运动员，专项发球练习，接球练习等等等。刷法也是一样，不能只做一遍，针对弱项要多练。

•  做题方法
  • 多看几遍题，或者和面试官去恩人，确保自己的理解是正确的。
  • 想所有可能的解题方法，同时比较时间和空间复杂度。
  • 做题
  • test case
• 切题方法
  • 第一遍
    • 5分钟。读题+思考。
    • 直接看答案。注意多解法，对比。
    • 背诵+默写好的答案。
  • 第二遍
    • 马上默写背诵的答案-->提交LeetCode (寻找反馈)
    • 多种解法对比体会。
  • 第三遍
    • 24小时后重新做一遍
    • 针对不同解法的不熟练的要专项练习
  • 第四遍
    • 一周后反复练习相同的题目
  • 第五遍
    • 面试前反复练习