微软面试题： LeetCode 300. 最长递增子序列 出现次数：2

题目描述：

 

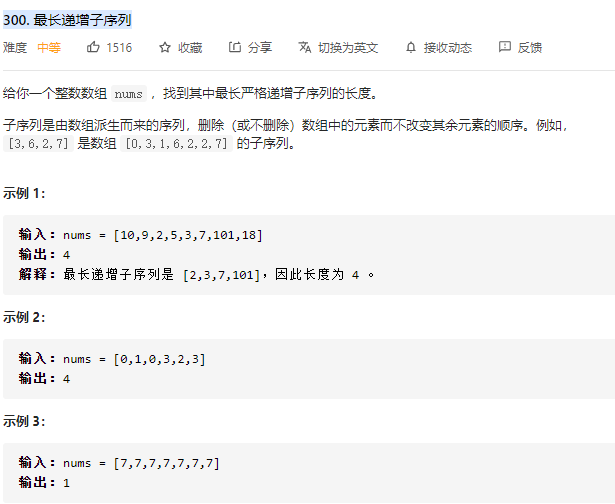
 解析：

参考 VV大神 的题解：

https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/dong-tai-gui-hua-er-fen-cha-zhao-tan-xin-suan-fa-p/

方法一： 动态规划    

//dp time: O(n^2)   memory :O(n)

1. 定义状态：

　　基于「动态规划」的状态设计需要满足「无后效性」的设计思想，可以将状态定义为「以 nums[i] 结尾 的「上升子序列」的长度」。

「无后效性」的设计思想：让不确定的因素确定下来，以保证求解的过程形成一个逻辑上的有向无环图。这题不确定的因素是某个元素是否被选中，

而我们设计状态的时候，让 nums[i] 必需被选中，这一点是「让不确定的因素确定下来」，也是我们这样设计状态的原因。

 

2. 状态转移方程：

       如果一个较大的数接在较小的数后面，就会形成一个更长的子序列。只要 nums[i] 严格大于在它位置之前的某个数，那么 nums[i] 就可以接在

这个数后面形成一个更长的上升子序列。

 

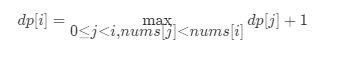
3. 初始化：

dp[i] = 1，11 个字符显然是长度为 11 的上升子序列。

 

4. 输出：

状态数组 dp 的最大值。

 

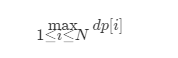
5  空间优化：

遍历到一个新数的时候，之前所有的状态值都得保留，因此无法优化空间。

代码：

//dp time: O(n^2)   memory :O(n)
    int lengthOfLIS(vector<int>& nums)
    {
        int res = 1;
        vector<int> dp(nums.size(),1);
        for(int i = 1; i < nums.size(); ++i)
        {
            for(int j = 0; j < i ;++j)
            {
                if(nums[j] < nums[i])
                {
                    dp[i] = max(dp[i],dp[j] + 1);
                }
            }
            res = max(res,dp[i]);
        }
        return res;
    }

 

方法二：dp  修改状态定义（同时用到了贪心算法、二分查找）

　　状态设计思想：依然着眼于某个上升子序列的结尾的元素，如果已经得到的上升子序列的结尾的数越小，那么遍历的时候后面接上一个数，

会有更大的可能构成一个长度更长的上升子序列。既然结尾越小越好，我们可以记录 在长度固定的情况下，结尾最小的那个元素的数值，这样定义

以后容易得到「状态转移方程」。

     1 .定义新状态（特别重要）

tail[i] 表示：长度为 i + 1 的 所有 上升子序列的结尾的最小值。

     数组 tail 也是一个严格上升数组。

    2. 状态初始化

  遍历第 1 个数 nums[0]，直接放在有序数组 tail 的开头 tail[0] = nums[0]。

    3.状态转移

3.1  在遍历数组 nums 的过程中，看到一个新数 num，如果这个数 严格 大于有序数组 tail 的最后一个元素，就把 num 放在有序数组 tail 的后面，否则进入第 2 点；

3.2  在有序数组 tail 中查找第 1 个等于大于 num 的那个数，用新数 num 替换；

   4. 输出：

有序数组 tail 的长度，就是所求的「最长上升子序列」的长度。

   5. 空间优化：

无法优化空间。

//dp time: O(n*logn)   memory :O(n)
    int lengthOfLIS(vector<int>& nums)
    {
        //tail[i]：当前长度为 i+1 的递增子序列中，结尾元素最小的递增子序列的结尾元素值
        vector<int> tail;
        tail.push_back(nums[0]);
        for(int i = 1; i < nums.size(); ++i)
        {
            if(nums[i] > tail.back())
            {
                tail.push_back(nums[i]);
            }
            else
            {
                int j = std::lower_bound(tail.begin(),tail.end(),nums[i]) - tail.begin();
                tail[j] = nums[i];
            }  
        }
        return tail.size();
    }