微软面试题： LeetCode 48. 旋转图像 出现次数：3

题目描述：

　　给定一个 n × n 的二维矩阵表示一个图像。将图像顺时针旋转 90 度。要求空间 O( 1 )

分析：

　　要求空间 O(1)  意味着必须在给定的 矩阵内通过交换元素的方式原地旋转矩阵。

第一步：分层

总体思路就是 对矩阵从外到内分层（如下图），从最外层环到最内层环逐层旋转。比如 5*5 矩阵可以分成下面的 3层。

 

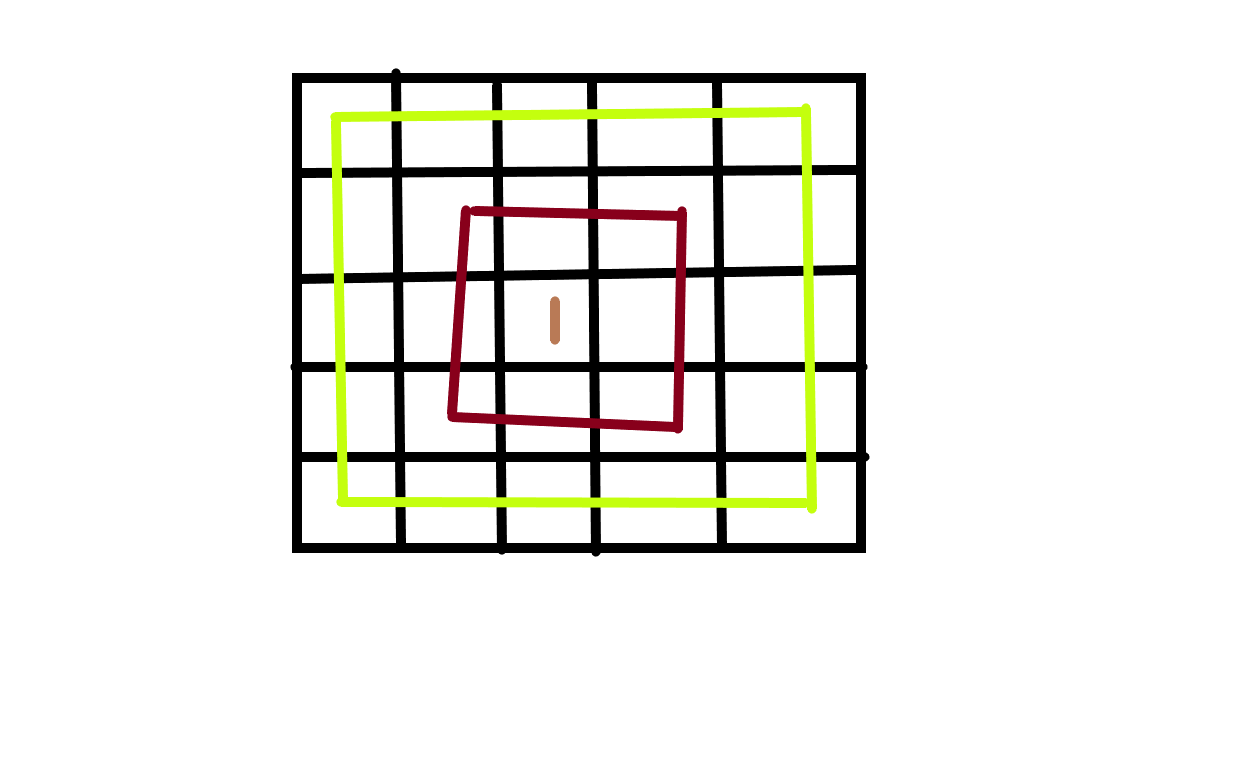
 第二步：4 个边角点坐标表示一环层的元素　

  　每一环层都可以用左上、右上、左下、右下 的 4个边角点表示环层内所有元素。由于是 n * n 矩阵,

可以定义两个变量p1, p2 表示 4个边角点，从最外环层开始，初始化  int p1 = 0，p2 = n - 1  四个边角点 

左上（p1,p1）、右上(p1,p2)、左下(p2,p1)、右下 (p2,p2)。

 

 

 

第三步：旋转每一环层

　　旋转的时候每 4 个对称的节点，进行交换操作，交换中需要用到一个临时变量。

如下图，对同一种颜色的数字，可以先用一个 临时变量  tmp 保存数字 1 位置的元素，

由于是 顺时针旋转 90度，将 位置 4 的元素移到 位置 1，将  位置 3 的元素移到位置 4，

将位置 2 的元素移到位置 3，将保存在 tmp 中的原位置 1 上的元素 移到位置 2。

待图上所有颜色的数字对应的位置都移动完成后，则当前层旋转完成，接着旋转里面一层的元素。

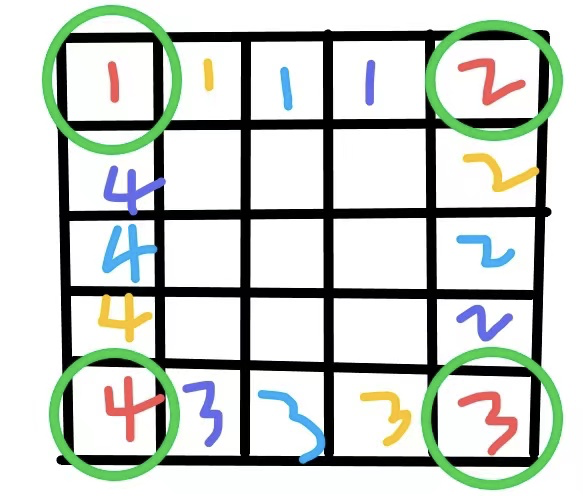
　　如下图，第一次旋转红色数字，第二次旋转黄色数字，第三次旋转蓝色数字，第四次旋转紫色数字。

可以看出，每次旋转的时候比上一次旋转偏移了一格。第一次旋转的四个点坐标分别为

左上（p1,p1）、右上(p1,p2)、左下(p2,p1)、右下 (p2,p2)。更一般地表达，对左上（p1,p1 +add）、

右上(p1+add,p2)、左下(p2-add,p1)、右下 (p2,p2-add)。当add = 0 表示第一次旋转，1 表示第二次旋转，

2 表示 第三次旋转，3表示第四次旋转。add >= 0 且 add + p1 < p2 。

 

 

 第四步：每次计算完一层之后，矩阵向内收缩一层，如图所示：

 

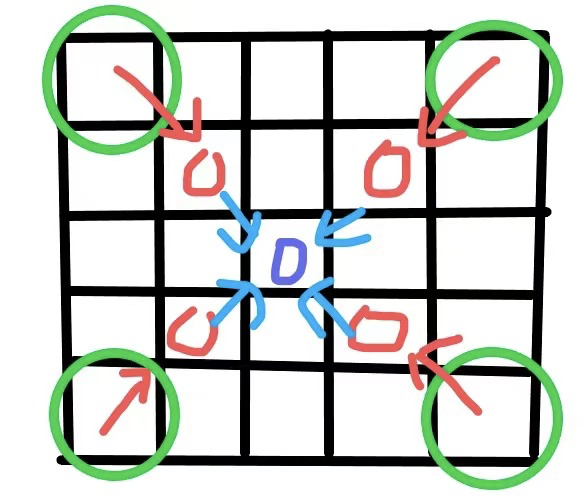
 　　经坐标变换：pos1 = pos1+1,pos2 = pos2-1 。四个边角点仍可表示为 左上（p1,p1）、

右上(p1,p2)、左下(p2,p1)、右下 (p2,p2)。矩阵收缩到最里面一层终止，终止条件：pos1 < pos2。

 

最终代码如下所示：

 

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) 
    {
        int pos1 = 0,pos2 = matrix.size() - 1;
        while(pos1 < pos2) //外层矩环 -> 内层矩环
        {
            int add = 0;
            while(add < pos2 - pos1) 
            {
                int tmp = matrix[pos2-add][pos1];
                matrix[pos2-add][pos1] = matrix[pos2][pos2-add];
                matrix[pos2][pos2-add] = matrix[pos1+add][pos2];
                matrix[pos1+add][pos2] = matrix[pos1][pos1+add];
                matrix[pos1][pos1+add] = tmp;
                ++add;
            }
            pos1 = pos1 + 1;
            pos2 = pos2 - 1;
        }
        return;
    }
};