离散概率论2
上文:离散概率论1
首先介绍一些必要的性质:
性质:
- 1.\(P (\Omega) =1,P(\emptyset) =0\)
- 2.\(P (A) =1-P(\bar{A} )\)
- 3.次可加性:\(P (A\cup B) =P(A)+P(B)\)或者说\(P (A+B) =P(A)+P(B)\)
- 4.可加性 \(若A\cup B =0,P(A+B)=P(A)+P(B)\)
那么可加性可逆吗?
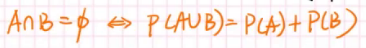
首先这一件事肯定正确:
\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)
如果\(A\cap B=\emptyset\)等价于\(P(A\cap B)=0\),这件事就对了。
可一个事件不可能发生和一个事件发生的概率为\(0\)显然是不一样的,由此我们可以看出次可加性才是最本质的。
独立性
两个事件之间的独立性:
独立性是概率里一个重要的定义:
- 1.两个事件独立:事件\(A\)与\(B\)相互独立的定义是\(P (AB) =P(A)P(B)\)
ps:对立不意味着独立,比如下面的例子:
eg1.1:抛硬币的正面和反面独立吗?
其实是不独立的:\(P(正)=1/2,P(反)=1/2,P(正反)=0\)
但是下面的这个例子呢?
eg1.2:抛两次硬币,第一次正面向上和第二次反面向上独立吗?
\(P(正)=1/2,P(反)=1/2,P(正反)=1/4\),我们发现竟然是独立的。
因为基本事件空间其实已经变了。设上面的基本事件空间为\(\Omega\),这个例子的其实是\(\Omega \times \Omega\)(笛卡尔积)
eg2

看着好像有点关系是吧?但我们发现\(P(A)=1/6,P(B)=1/6,P(AB)=1/36\),\(A\),\(B\)是独立的
多个事件相互独立
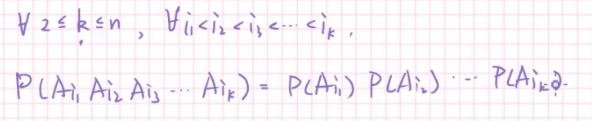
也就是任取\(2~n\)个事件,它们之间都相互独立。
看的出来,多个事件相互独立要求很强。
多个事件两两独立
从定义就能看出来,只需要任取两个使得这两者独立就行了。
显然的,相互独立可以推出两两独立。
两两独立但不相互独立
这种情况虽然看起来回发生,但还是需要构造出一组才行。
有一个神奇的构造。

这个色子有四面。一面是红,一面黄,一面蓝,一面有红有黄又蓝,我们可以得出:
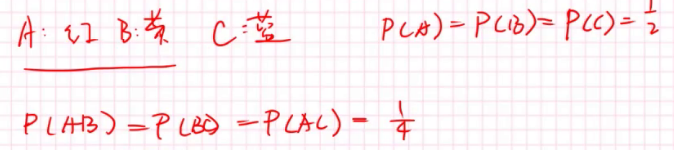
这足以证明两两独立,但:
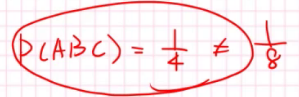
所以不相互独立。
随机变量(random variable)
我们用X表示随机变量。
对于每一个X相对的有一个概率
\(P(X=a_i)=P(i)\)
下图就是随机变量的一个分布列;
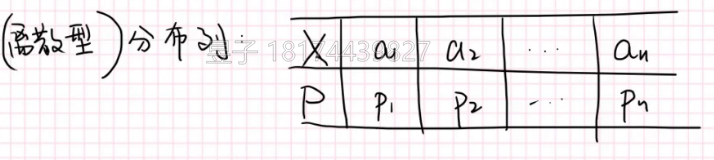
那么分布列要满足下面的限制:
- 1.\(\sum P_i=1\)
- 2.\(P_i>=0\)
举个例子,记抛硬币正面向上为1,反面向上为0,分布列就是这样的:
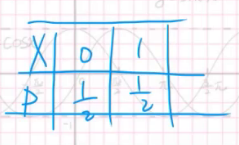
如果还没懂,看投色子的分布列:
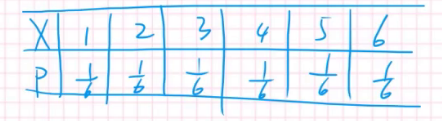
可是我们还没有对它下定义:
定义:
\(X\):\((\Omega,F)->(R,B)\)
这里默认的随机变量\(X\)在实数域中,若果为整数把\(R\)换掉就行了。
解释一下这个式子。\(X\)其实是基本事件空间上的一个事件一个对\(R\)生成的\(Bodel\)域(可以把\(Bodel\)域看成\(R\)中可测量的子集)的对应,\(X\)是一个函数,一个从\(\Omega\)向\(R\)的一个映射。
谈概率的可行性:
先在我们再来思考为什么我们可以研究\(x=1\)的概率,其实是在研究下图的测度。
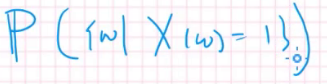
分布
0-1分布(两点分布)
对于一个事件,结果只有\(A\)或\(\bar A\),此时称为Bernoulli事件。
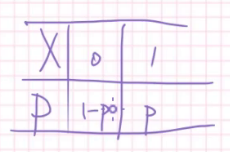
那么两点分布的期望:
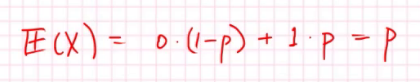
方差:
方差显示了偏离期望的程度。
现在我们可以计算方差(偏离期望越大方差越大,第一行是方差的计算式):
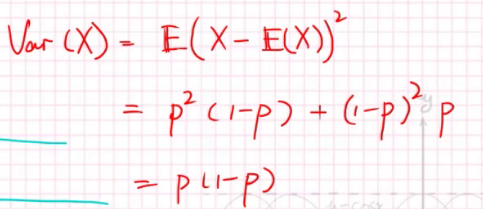
方差有可能不存在吗?可能。
比如下面的例子:
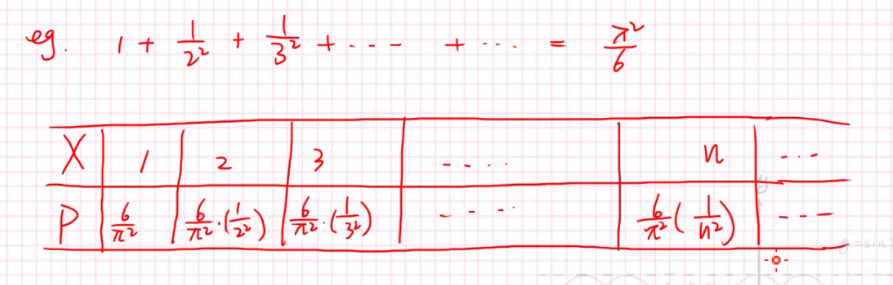
相信你一眼就能看出来:
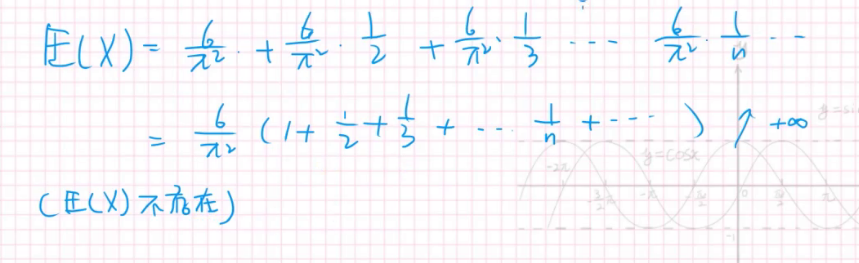
期望都不存在了,肯定是不存在方差的。
这样就有一个显然的结论:
- 1.如果期望不存在,方差一定不存在。
ps:这个结论是不可逆的
二项分布:
二项分布:X记成n次0-1分布中A发生的次数。
举个抛硬币的例子,我们抛十次硬币,把正面向上的次数记作X,得到分布列。
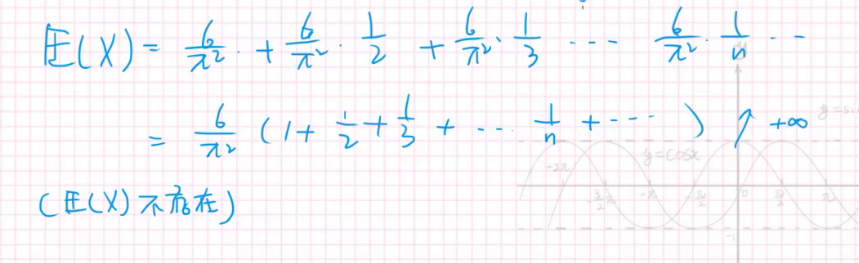
分布列很好算:
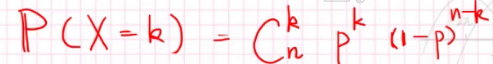
对于P(x=k),在n次里选k次正面向上,一次正面向上的概率是p,其他的n-k次都应该是反面,一次反面的概率是1-p。
而它的期望如下:
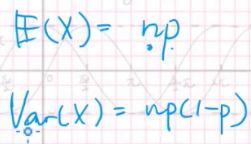
我们把二项分布记作:
\(X~B(n,p)\),n是试验次数,p是一次概率。
Posson分布(泊松分布)
泊松分布其实是二项分布的极限。
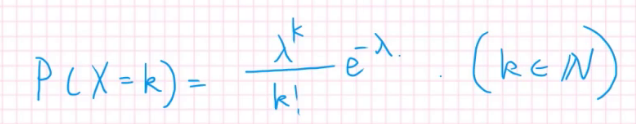
它的概率和是1,用泰勒展开可以证明。
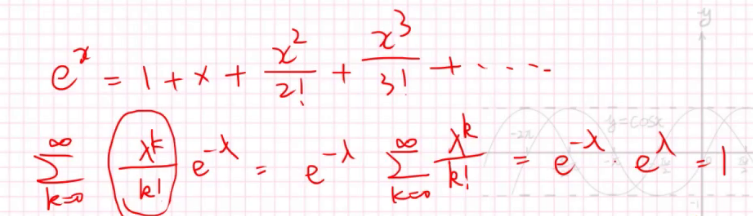
而它的期望是:
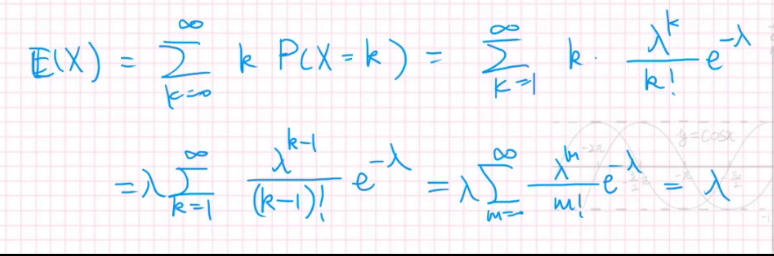
所以$\lambda $越大,期望越大。
还有个神奇的结论:
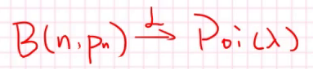
我们把它记作\(X~Poi(\lambda )\)

