离散概率论1

起源：

有两个赌徒，7局4胜，赢了的获得1000元。结果只进行了一半就不得已结束。甲赢了3局，乙赢了1局，怎么分钱？

最公平的分发就是按获胜的概率分，如果继续进行，甲有87.5%的概率获胜，分得875元，乙分得125元。

这是最初的概率，但是生活中概率有很多滥用：降水概率（频率），色子（概率），硬币（概率），新冠感染率（频率）。

所以有必要先区分一下概率。

频率和概率

频率是指发生的次数比上总次数。
概率是一个系统决定的先验。

通俗一点就是概率是确定的，而频率是计算得来的。

事件与概率（不严谨）

经典概率论：概率是事件发生的可能性大小。（其实这是不严谨的）
为什么不严谨？
因为没有数学名词，都是用的生活词汇。
先来看看经典概率论：
事件分为：

• 1.确定时间（结果唯一）
• 2.随机事件（结果不唯一）
  而确定事件又分为：
• 1.必然事件
• 2.不可能事件
  我们把事件记作A，概率记作P(A)
  若果A是必然事件，那么P(A)=1；
  若果A是不可能事件，那么P(A)=0
  反过来，下面的式子还对吗？也就是说等价吗？
  
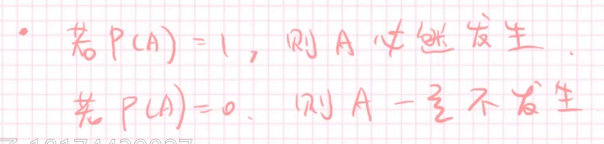
  我们考虑这样一个问题。我现在有一个圆，投中圆心的概率是多少？

是圆心的面积除以圆的面积。圆有面积，可是圆心没有，也就是概率为0.但是显然可以投中圆心，所以上文的式子是错的。这就可以再次证明经典概率论是不严谨的。

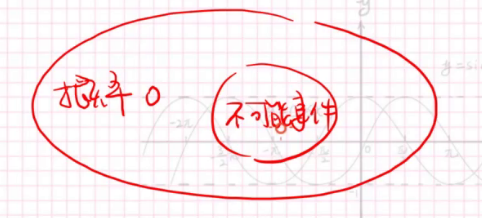
我们只能知道0<=P(A)<=1

新的概率

首先我们有必要知道一些前置定义。

基本事件空间：

事件所有可能的结果的集合
ps:集合，终于出现数学语言了。

古典概型：

古典概型：基本事件空间元素有限，每种情况等可能发生。
在古典概型下：P(A)=A包含的情况个数/所有情况个数。古典概型的限制是

• 1.受限于基本事件空间，情况要有限。
• 2.每种情况要等可能
  举个例子，抛硬币正面向上的概率。
  你会说50%。
  可是有没有可能立在桌子上，这样到底算不算正面呢。
  发现问题了吗？我既没有定义基本事件空间，也没有说怎么算正面向上。

几何概型：

几何概型：基本事件空间情况无穷多，概率正比于事件的几何测度。
给一个例子：

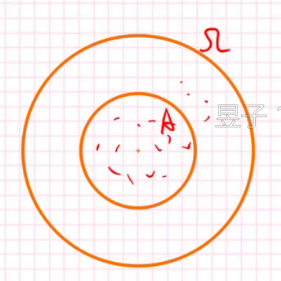
小圆的半径是r,大圆的是R那么投中小圆里的概率是多少。

显然P(A)是r的平方除以R的平方（原谅Latex手残党），这个时候古典概型就无能为力。

几何概型的优势就是能解决一些看着很巧妙，但实际很难处理的问题。

比如下面的问题：

给定一个长度为1的棍子，分成3份，问这三份正好可以围成三角形的概率。
首先我们来刻画这个时间，设第一段的长度为x，第二段为y，第三段为1-x-y那么根据两边之和大于第三边可以列出三个要求。

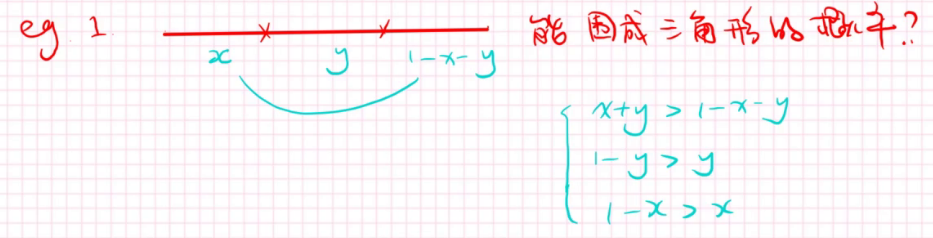
那么基本事件空间呢，就是这三者要小于1。

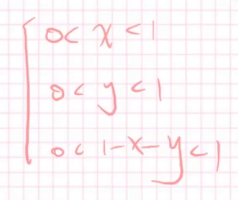
实际上这两个不等式组都是对x,y的限制，我们把x,y当成坐标轴，粉色的三角形就是基本事件空间，蓝的则是围成三角形的基本事件。

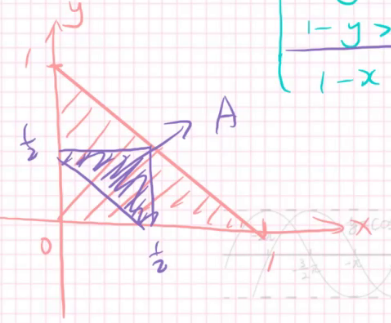
虽然解的结果x是取不到1/2的，但是这一条边可以忽略不计。

现代概率论

首先对于基本事件空间：

• 1.不用等可能
• 2.可以无限，也可以有限

事件域：

在事件域中可以谈论概率。
它满足：

• 1.是基本事件空间的子集
• 2.全集在事件域里
• 3.若A在事件域里，A的补集也在事件域里
• 4.若A,B在事件域里，A和B的并集也在事件域里
• 5.事件域不一定是唯一的

什么是概率：

概率（P）是$\Omega $上的一个测度，满足：

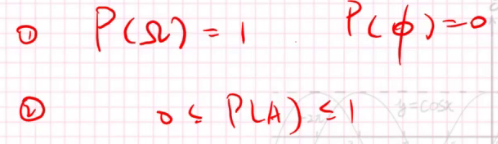
现在我们再来看几何概型：
只要让$\Omega $无限比如实数集，它也就是一个测度。

测度的限制

• 1.单调性，A是B的子集P(A)<=P(B)
• 2.次可列可加性：
  

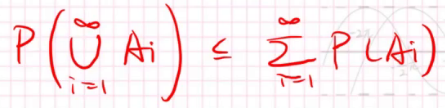
有了现代概率论，现在所有的概率都可以抽象为一个三元组：\((\Omega,F,P)\)
\(\Omega\)是基本事件空间，\(F\)是事件，\(P\)是\(F\)发生的概率。
下文：离散概率论2