组合数学初步
入门:
先介绍三个简单的技术
插板法:
直接插板:
看下面的问题:
eg1:
我们考虑有
这两个板子怎么插呢不难想到——插在
答案是
先转化,再插板(一一对应):
eg2:
这个问题不好直接插板。因为可能有零的出现,多个板子可以插在同一个地方。你考虑这样一件事,就是说下面这个问题的解其实和上面的问题一样:
是不是豁然开朗。我令:
独立完成下面的问题:
eg3:
答案
原问题可以化为:(x+2)+(y+1)+(z+3)=20,其中(x+2),(y+1),(z+3)为正整数,求有多少组解。
捆绑法:
eg1:
有
如果没有
看下面的问题:有
这个问题直接插板就行了。
进阶:
Catalan 数(卡特兰数)
引入:
先看几个问题:
eg1.
有
eg2.
一个人从原点出发,若当前处于
eg3.
有一个
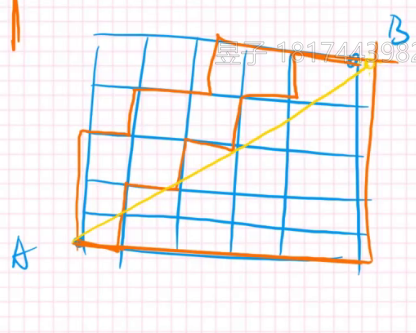
从
eg4.
发现了吗,这其实是一个问题,卡特兰数的模型是这样的;
- 从原点出发,向上走
计算Catalan 数
先不考虑只在正半轴的条件,方案数就是
先看下面的图,这种方案显然不合要求:
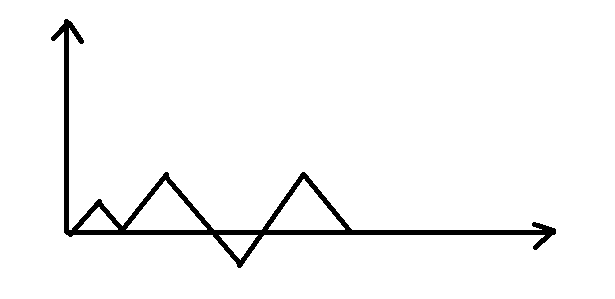
记得上文插板法一一对应的思想吗?我们找到这条不合要求的线,把它第一次到x轴一下之后的部分关于y=-1对称。
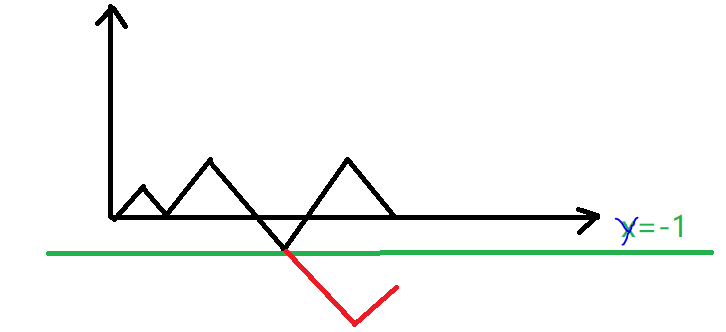
显然对称后的轨迹最后一定停留在(2* N,-2),也就是每一条不合要求的线都可以转化为一条从原点出发,最后到x=-2的轨迹。不难看出,反过来转化也是成立的。即这两者是一一对应的。现在只要算出有多少种情况最后停留在直线x=-2上,这很简单,2* N次选择N+1次向下。
这样我们得到了最朴素的计算公式:
再稍微推导一下:
$=\frac{(N+1)(2* N)!}{(N+1)N!N!}-\frac{N(2 N)!}{ N(N+1)!(N-1)!} $



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】