leetcode剪绳子

问题

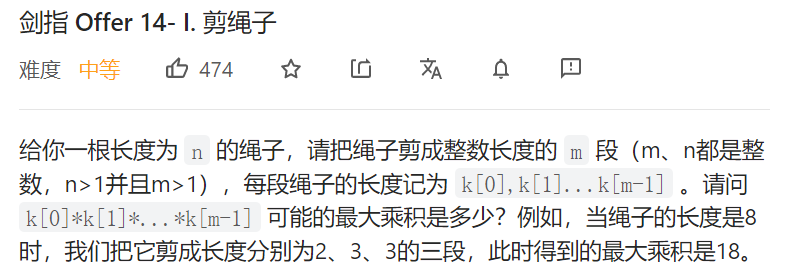
这其实是一道简单的数学问题： \(a_1+a_2+...+a_m = n\)，其中 m 为正整数，求 \(a_1*a_2*a_3*...a_m\) 的最大值。

数学推导

首先根据基本不等式的推广有：

\[\frac{a_1+a_2+...+a_m}{m} \ge \sqrt[m]{a_1a_2...a_m } \]

不等式在 \(a_1=a_2=...=a_m\) 时成立，说明要想乘积最大，每段必须相等。设每段长度为 x,即求：\(x ^{\frac{n}{x}}\) 的最大值（x>0)

\[y = x ^{\frac{n}{x}} \\ lny = \frac{n}{x}lnx= \frac{nlnx}{x} \]

两侧求导：\(\frac{1}{y}y'=n\frac{1 - lnx}{x}\)，所以 \(y'=n\frac{1-lnx}{x}x^{\frac{n}{x}}\),极大值点 \(x = e\)，由于该问题中 x 为正整数，且 \(e \in (2,3)\),故最大值在 \(x = 2\) 或者 \(x = 3\) 取到,由于 \(f(x)=lnx\) 是单调递增的，故分别将 2 和 3 带入 \(lny\)：

\[lny(2)= n \frac{ln2}{2} , \ lny(3)=n \frac{ln3}{3} \]

\[\frac{lny(3)}{lny(2)}=\frac{2ln3}{3ln2}= \frac{ln9}{ln8}>1 \]

发现将绳子每段长度为 3 时候乘积最大，考虑到部分数不能整除 3，所以单独考虑：

• 除以 3 余数为 1，则将最后一段和前一段保留合并为 4
• 余数为 2，由于保留后，最后两端乘积为 6，不保留则为 5，故最后一段为 2

代码实现

class Solution {
public:
    int cuttingRope(int n) {
        if(n <= 3){
            return n-1;
        }
        int cnt = n / 3;
        int mod = n % 3;
        if(mod == 0){
            return pow(3,cnt);
        }
        else if(mod == 1){
            return pow(3,cnt-1) * 4;
        }
        else{
            return pow(3,cnt) * 2;
        }
    }
};

剪绳子问题2

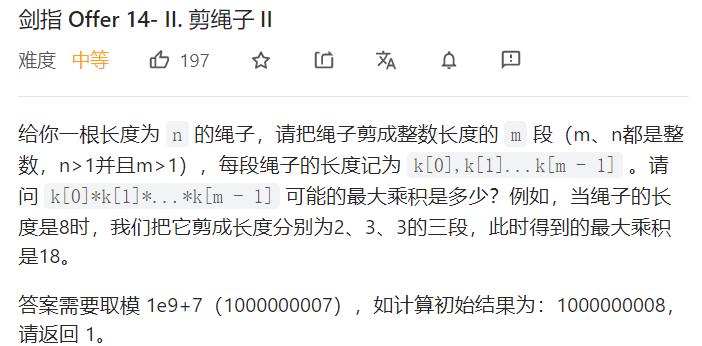
这里需要考虑数据越界的问题，直接用库函数Math.pow会越界,故自行处理幂运算

class Solution {
    private static int  MOD = (int)1e9+7;
    public int cuttingRope(int n) {
        if(n <= 3)  return n - 1;
        int m = n / 3;
        int mod = n % 3;
        long res = quickPow(3,m-1);
        if(mod == 0) return (int)(res * 3 % MOD);
        else if(mod == 1) return (int)(res * 4 % MOD);
        else{
            return (int)(res * 6 % MOD);
        }
    }

    public int quickPow(long x, int m){
        long res = 1;
        while(m > 0){
            if((m&1)==1) res = (res * x) % MOD;
            x =  (x * x) % MOD ;
            m >>= 1;
        }
        return (int)res;
    }
}