匈牙利算法&KM算法

二分图匹配

二分图：交集为空的节点集合\(U，V\)，二者通过无向边连接，且同一集合内的任意两个节点之间不存在边。

匹配：二分图中节点不重复的边集，顾名思义，最大匹配就是边集最大的匹配。

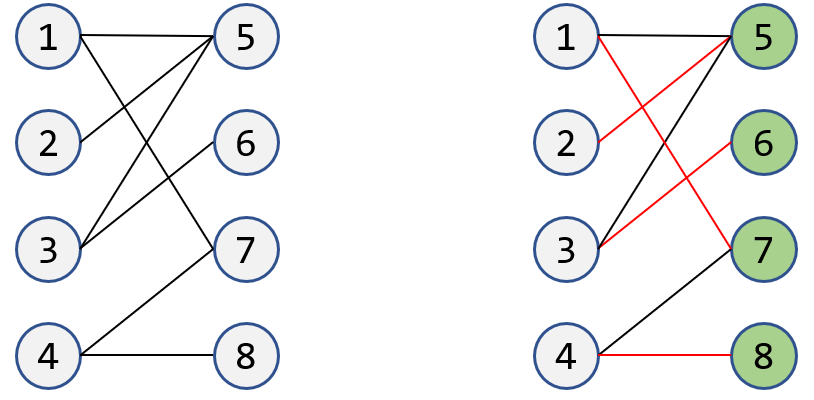
匈牙利算法

匈牙利算法可较为简单地解决二分图的最大匹配问题。生活场景中，如相亲节目中希望让尽可能多的男女结合为情侣。算法流程可看这个帖子：(107条消息) 趣写算法系列之--匈牙利算法_Dark_Scope的博客-CSDN博客_匈牙利算法。下面给出从二分图左边节点出发寻找增广路径以及最大匹配的代码（同样也可以从二分图右边，即为女生找男生的角度完成最大匹配）

int match[maxm];
int used[maxm];

bool dfs(int boy){
	for(int  girl: adj[boy]){   //adj[boy]表示男生心仪的女生序列
		if(!used[girl]){  //该女生没被其他男生标记过
			used[girl] = 1;
			if(match[girl] == -1 || dfs(match[girl])){
				match[girl] = boy;
				return true;
			}
		}
	}
	return false;
}

void max_matching(){
	std::fill(match, match+sizeof(match)/sizeof(int), -1);
	int num_match = 0;
	for(int boy: boy_list){
		memset(used,0,sizeof(used));
		if(dfs(boy){
			num_match += 1;
		}
	}
}

KM算法

问题：女生对不同男生存在不同的好感度（僧多肉少的时代，不考虑男生的意愿了🤣），若希望完成的匹配好感度总和最大，又当如何匹配呢？

KM算法用于求解完美匹配下，最大权重匹配，相应的程序如下：

const int MAXN = 305;
const int INF = 0x3f3f3f3f;

int love[MAXN][MAXN];   // 记录每个妹子和每个男生的好感度
int ex_girl[MAXN];      // 每个妹子的期望值
int ex_boy[MAXN];       // 每个男生的期望值
bool vis_girl[MAXN];    // 记录每一轮匹配匹配过的女生
bool vis_boy[MAXN];     // 记录每一轮匹配匹配过的男生
int match[MAXN];        // 记录每个男生匹配到的妹子 如果没有则为-1
int slack[MAXN];        // 记录每个汉子如果能被妹子倾心最少还需要多少期望值

int N;


bool dfs(int girl)
{
    vis_girl[girl] = true;

    for (int boy: adj[girl]) {       //遍历每个女生的备胎

        if (vis_boy[boy]) continue; // 每一轮匹配 每个男生只尝试一次

        int gap = ex_girl[girl] + ex_boy[boy] - love[girl][boy];

        if (gap == 0) {  // 如果符合要求
            vis_boy[boy] = true;
            if (match[boy] == -1 || dfs( match[boy] )) {    // 找到一个没有匹配的男生 或者该男生的妹子可以找到其他人
                match[boy] = girl;
                return true;
            }
        } else {
            slack[boy] = min(slack[boy], gap);  // slack 可以理解为该男生要得到女生的倾心 还需多少期望值 取最小值 备胎的样子【捂脸
        }
    }

    return false;
}

int KM()
{
    memset(match, -1, sizeof match);    // 初始每个男生都没有匹配的女生
    memset(ex_boy, 0, sizeof ex_boy);   // 初始每个男生的期望值为0

    // 每个女生的初始期望值是与她相连的男生最大的好感度
    for (int i = 0; i < N; ++i) {
        ex_girl[i] = love[i][0];
        for (int j = 1; j < N; ++j) {
            ex_girl[i] = max(ex_girl[i], love[i][j]);
        }
    }

    // 尝试为每一个女生解决归宿问题
    for (int i = 0; i < N; ++i) {

        fill(slack, slack + N, INF);    // 因为要取最小值 初始化为无穷大

        while (1) {
            // 为每个女生解决归宿问题的方法是 ：如果找不到就降低期望值，直到找到为止
            // 记录每轮匹配中男生女生是否被尝试匹配过
            memset(vis_girl, false, sizeof vis_girl);
            memset(vis_boy, false, sizeof vis_boy);

            if (dfs(i)) break;  // 找到归宿 退出

            // 如果不能找到 就降低期望值
            // 最小可降低的期望值
            int d = INF;
            for (int j = 0; j < N; ++j)
                if (!vis_boy[j]) d = min(d, slack[j]);

            for (int j = 0; j < N; ++j) {
                // 所有访问过的女生降低期望值
                if (vis_girl[j]) ex_girl[j] -= d;

                // 所有访问过的男生增加期望值
                if (vis_boy[j]) ex_boy[j] += d;
                    // 没有访问过的boy 因为girl们的期望值降低，距离得到女生倾心又进了一步！
                else slack[j] -= d;
            }
        }
    }

    // 匹配完成 求出所有配对的好感度的和
    int res = 0;
    for (int i = 0; i < N; ++i)
        res += love[ match[i] ][i];

    return res;
}

现实中，往往是多名女生倾心于少数优质的男生，造成部分女生成为剩女，同样有的男生也要成为光棍，这种不能完美匹配问题，KM似乎无法解决。但通过增加一些额外边，实现完美匹配。例如根据问题的不同，增加一些权重为\(\infty\)或者0的边。如论文Controllability of multiplex, multi-time-scale networks中给出求解最大环覆盖的节点，是通过额外增加权重为1的自环实现完美匹配，继而可利用KM算法求解。