第一二章：概述&信息表示与处理

第一章 计算机系统漫游

程序翻译过程

像 c 语言源文件这样，只由 ASCII 码字符构成的文件为 文本文件 ，所有其他文件为 二进制文件 。GCC 编译器中，一个 hello.c 文件经过以下四个阶段后被翻译为可执行文件：

flowchart LR A[hello.c]--预处理--->B[hello.i] B--编译--->C[hello.s] C--汇编--->D[hello.o] D--链接--->E[hello]

• 预处理：处理 # 开头的命令，如 #include 将被包含的头文件的内容插入程序中，#define直接替换宏定义
• 编译：将文件文件 hello.i 翻译为汇编程序 hello.s
• 汇编：将 hello.s 翻译为机器指令，得到目标文件
• 链接：合并其他目标文件，得到可执行程序

程序执行过程

典型系统硬件组成

• 总线：一组电子导管，携带信息在各部件传递
• I/O 设备：一般包括鼠标键盘，显示器，磁盘，它们有适配器和 I/O 总线相连
• 主存：临时存储设备，由动态随机存储器 DRAM 芯片组成
• 处理器： CPU，负责解释执行主存中的指令

执行 ./hello 后，shell 程序读取字符到寄存器，并放入内存，处理器执行机器指令，字符串存主存复制到寄存器文件，再复制到显示设备。

高速缓存至关重要

主存到寄存器间复制造成开销，二者数据存取速度相差较大，为了处理这种差异，在二者间采用了高速缓存存储器（cache memory)。

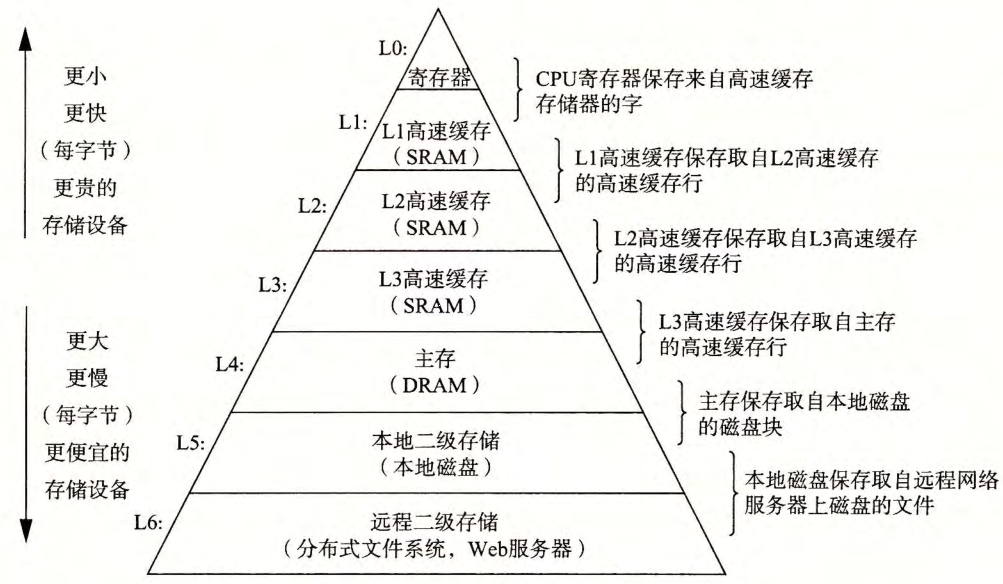
操作系统管理硬件

操作系统两个基本功能：

• 防止硬件被滥用
• 控制设备

操作系统通过进程，虚拟内存和文件实现两个基本功能

进程与线程

进程是对正在运行的程序的一种抽象，是计算机科学最重要和最成功的概念之一。现代系统，一个进程实际上可由多个线程的执行单元组成，它们共享同样的代码和全局数据，一般而言，线程比进程更高效。

虚拟内存

每个进程看到的内存是一致的，都认为自己独占内存（假象）。

重要主题

并发和并行

• 线程级：传统的的并发是通过交替执行实现，多核处理器可同时执行不同线程，实现并行
• 指令级：采用流水线技术同时处理多条指令

第二章 信息的表示和处理

信息存储

多数计算机使用字节（8 位）作为最小的可寻址单元，二进制对人而言不友好，和十进制转化麻烦，替代方法是十六进制，二进制 → 十六进制转化：二进制从低位开始，每 4 位合并为一个 16 进制数。

计算机中字长（word size)表示指针数据得标称大小（normal size),因为虚拟地址是用一个字编码的。

大/小端法存储

• 小端法：内存中最低有效字节在前（大多数系统）
• 大端法：最高有效字节在前

以存储 0x012345678 为例

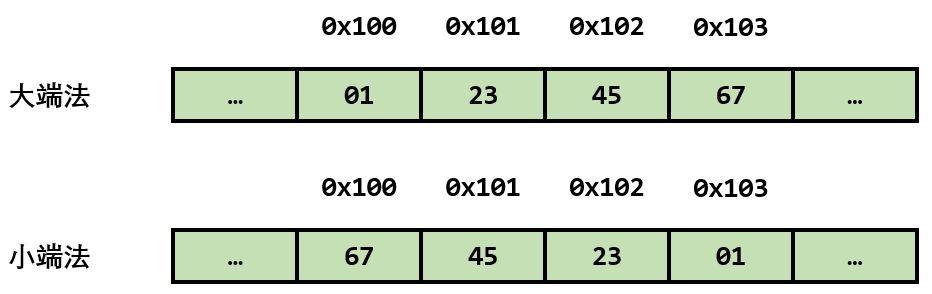
c 语言中的位级运算

与（&），或（|），取反（~），异或（^).

表达式	二进制表达式	二进制结果	十六进制结果
~0x41	~[0100 0001]	[1011 1110]	0xBE
~0x00	~[0000 0000]	[1111 1111]	0xFF
0x69 & 0x55	[0110 1001] & [0101 0101]	[0100 0001]	0x41
0x69	0x55	[0110 1001] & [0101 0101]	[0111 1101]

利用位运算，单个字符（a-z,A-Z)和 0x20（[0010 0000]）异或，可以实现大小写翻转，因为大小写字符的 16 进制数相差 0x20,二进制第 6 位为 1 或者 0 与 1 做异或，刚好翻转。

c 语言中的逻辑运算

或（||），&&（与）和非（!）

！0x40 = 0
！0x00 = 1
0x69 && 0x55 = 1
0x69 || 0x55 = 1

c 语言中的移位运算

两种移位操作：

• 算数左（右）移：如 \(x >> k\)，把 x 向右移动 k 位，且在左边补上 k 个符号位
• 逻辑左（右）移：移动补 0

c 语言并没有明确规定对于有符号数使用何种位移操作，实际上几乎所有的编译器采用的都是算数左右移，Java 对此有明确规定，x >> k 是算术右移，x >>> k 是逻辑右移。k 如果很多，需要对 k 求模，如 int 类型数据，k mod 32.

有符号数编码

c/c++ 支持无符号数，java 只有有符号数。 假设整型数据有 www 位，可以用向量表示 \(x=[x_{w-1},x_{w-2},...,x_0]\),无符号编码的定义：

\(B2U_w(x)=\sum_{i=0}^{w-1}{x_i2^i}\)

补码编码

常用补码编码表示有符号数，对于向量 x=[xw−1,xw−2,...,x0]x=[x_{w-1},x_{w-2},...,x_0]x=[x​w−1​,x​w−2​,...,x​0​]，其定义如下：

\(B2T_w(x)=-x_{w-1}2^{w-1}+\sum_{i=0}^{w-2}x_i2^i\)

最高位 \(x_{w-1}\) 为符号位，为 1 表示负数，为 0 表示正数，权重为 \(2^{w-1}\)。

• \(B2T_4([0001])=-0\times2^3+0\times2^2+0\times2^1+1\times2^0=0+0+0+1=1\)
• \(B2T_4([1011])=-1\times2^3+0\times2^2+1\times2^1+1\times2^0=-8+0+2+1=-5\)
• \(B2T_4([1111])=-1\times2^3+1\times2^2+1\times2^1+1\times2^0=-8+4+2+1=-1\)

总结一句：正数和原码同，负数为除去符号位的原码减去最高位的权重。

有符号数与无符号数之间的转换

c 语言允许不同类型的数据之间进行强制类型转换。

  short int a = -12345;
  unsigned  short int b = (unsigned short)a;
  printf("a=%d b=%u\n",a,b);     // a=-12345 b=53191

a 的二进制补码为：1100 1111 1100 0111，强制转换位值不变，只是解释方式不同，转为无符号数：

\(2^{15}+2^{14}+2^{11}+2^{10}+2^{9}+2^{8}+2^7+2^6+2^2+2^1+2^0=32768+16384+2048+1024+512+256+128+64+4+2+1=53191\)。

补码转无符号数：

\(T_{2} U_{w}(x)=\left\{\begin{array}{l}x+2^{w},x<0 \\ x, x>0\end{array}\right.\)

如-12345 利用此公式计算：\(2^{16}-12345=65536-12345=53191\)

扩展一个数的位表示

• 无符号数零扩展：即高位补 0
• 补码数的符号位扩展：高位不符号位

整数运算

无符号数加法

对于无符号数 x,y,满足 \(0 \le x,y < 2^w\)，有

\(x+y=\left\{\begin{array}{l}x+y, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x+y<2^w \\ x+y - 2^w, \ \ \ \ \ \ \ 2^w \le x+y < 2^{w+1}\end{array}\right.\)

   unsigned  char a = 255;
   unsigned  char b = 255;
   unsigned  char sum = a + b;     // 510 - 256 = 254
   printf("%u\n",sum);             //254

补码加法

对满足 \(-2^{w-1}\le x,y<2^{w-1}\) 的整数 x,y:

\(x+y=\left\{\begin{array}{l}x+y - 2^w, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x+y \ge 2^w \\ x+y, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -2^{w-1} \le x+y < 2^{w-1} \\ x+y + 2^w, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x+y <-2^{w-1}\end{array}\right.\)

正溢出就减去 \(2^w\),负溢出就加上 \(2^w\)

无符号乘法

对于无符号数 x,y，满足 \(0 \le x,y < 2^w\)，有：

\(x*y=(x\times y) \text{mod} \ 2^{w}\)

补码乘法

对满足 \(-2^{w-1}\le x,y<2^{w-1}\) 的整数 x,y：

\(x*y=U2T_w((x\times y) \text{mod} \ 2^{w})\)

现将其视为无符号数，乘积模 \(2^w\),注意最后转为有符号数可能有个截断操作。

char a = 127;
char b = 126;
char c = a * b;    // -126
printf("%d\n",(char)(127*126 % 256));  // - 126
printf("%d\n",c); 

浮点数

二进制小数

形如 \(b_m...b_1b_0.b_{-1}b_{-2}...b_{-n}\) 的二进制数，其表示的十进制数为：

\(b=\sum_{i=-n}^{m}b_t\times2^{t}\)

二进制小数并不能准确表示某些小数，如 10 进制的 0.1,无法用二进制准确表示。

IEEE 浮点数

IEEE 浮点标准表示一个数：\(V = （-1）^s\times M \times 2^{E}\)

• 符号：\(s\) 为 0 表示正数，1 表示负数
• 尾数：\(M\) 为二进制小数，范围为 \(1 \sim 2-\varepsilon\) 或者 \(0 \sim 1-\varepsilon\)
• 阶码：\(E\) 对浮点数加权，且 \(E\) 可能是负数

浮点数三个字段编码：

• 一个符号位单独编码符号 sss
• \(k\) 位阶码字段 \(exp=e_{k-1}...e_1e_0\) 编码阶码 \(E\)
• n 位小数字段 \(frac = f_{n-1}...f_1f_0\) 编码尾数 \(M\)

c 语言中浮点数表示：

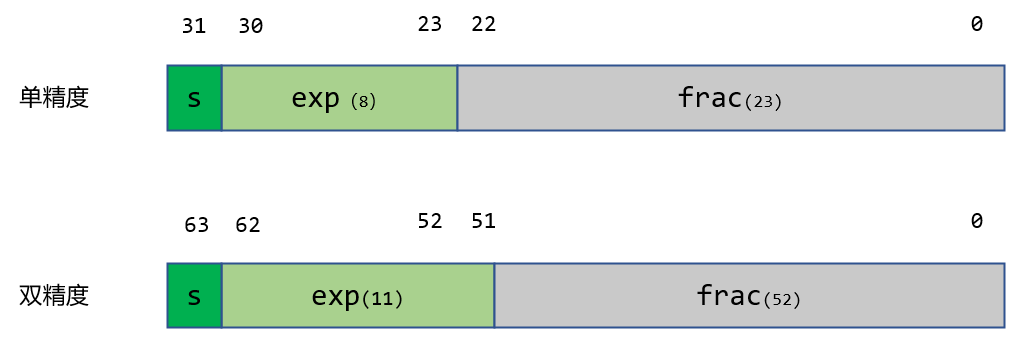
根据 exp 值，被编码的数分为三类：

规格化数

• exp 的位模式不全为 0 或者 1，阶码以偏置量表示 \(E=e-{Bias}\)，其中 \(Bias\) 单精度为 \(2^7-1=127\)，双精度为 \(2^{10}-1=1023\)，\(e\) 就是 \(exp\) 的位模式的无符号数
• 小数字段 frac 被解释为小数值 f，其中 \(0\le f<1\),尾数 \(M = 1 +f\)，隐藏了相同的第一位数 1

非规格化数

• 阶码全为 0，此时阶码值 \(E=1−Bias\)
• 尾数值 \(M=f,\) 不包含开头的 1

非规格化的数可表示 0.0,即小数域，阶码全为 0，还可以表示非常接近 0 的数

特殊值

阶码全为 1

• 小数位全为 0：表示无穷，\(s=0\) 表示 \(+ \infty\)，s=1 表示 \(-\infty\)
• 小数位不全非 0：如除以 0 溢出没结果为 NaN

数据示例：8 位浮点格式，k=4 的阶码位，n=3 的小数位(\(Bias=2^3-1=7\))

描述	位表示	\(e\)	\(E\)	\(f\)	\(M\)	值
0	0 0000 000	0	-6	0	0	0
最小非规格化数	0 0000 001	0	-6	\(\frac{1}{8}\)	\(\frac{1}{8}\)	\(\frac{1}{8} \times 2^{-6}\)
最大非规格化数	0 0000 111	0	-6	\(\frac{7}{8}\)	\(\frac{7}{8}\)	\(\frac{7}{8} \times 2^{-6}\)
最小规格化数	0 0001 000	1	-6	0	\(\frac{8}{8}\)	\(1\times 2^{-6}\)
最大规格化数	0 1110 111	14	7	\(\frac{7}{8}\)	\(\frac{15}{8}\)	\(\frac{1920}{8}\)
无穷大	0 1111 000	—	—	——	——	\(+ \infty\)

注意上面的最大非规格化数与最小规格化数平滑过渡，正是通过非规格化数的阶码 \(E=1−Bias\) 实现的。