Codeforces Round #329 (Div. 2) D. Happy Tree Party(LCA+并查集)
题目链接
题意:就是给你一颗这样的树，用一个$y$来除以两点之间每条边的权值，比如$3->7$，问最后的y的是多少，修改操作是把权值变成更小的。
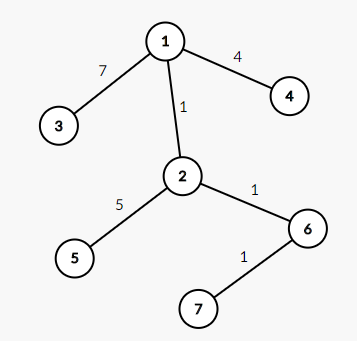
这个$(y<=10^{18})$除的权值如果是$>=2$，那么最多除60几次就变成0了，问题关键是路径上会有好多1存在，这时候我们可以用并查集把他们并到一块，这样就能跳着查了。
具体查法：
从$u$到$LCA(u,v)$，路径上除一遍。
从$v$到$LCA(u,v)$，路径上除一遍。
修改操作如果变成1，就与前面的点合并。
1 #include <iostream> 2 #include <algorithm> 3 #include <cstdio> 4 using namespace std; 5 6 typedef long long ll; 7 const int maxn = 2e5 + 10; 8 ///加边 9 int cnt = 0, h[maxn]; 10 struct edge 11 { 12 int to, pre; 13 ll v; 14 } e[maxn << 1]; 15 void add(int from, int to, ll v) 16 { 17 cnt++; 18 e[cnt].pre = h[from]; ///5-->3-->1-->0 19 e[cnt].to = to; 20 e[cnt].v = v; 21 h[from] = cnt; 22 } 23 ///LCA 24 int dist[maxn]; 25 int dep[maxn]; 26 int anc[maxn][33]; ///2分的父亲节点 27 ll len[maxn]; 28 void dfs(int u, int fa) 29 { 30 for(int i = h[u]; i; i = e[i].pre) 31 { 32 int v = e[i].to; 33 if(v == fa) continue; 34 dist[v] = dist[u] + e[i].v; 35 dep[v] = dep[u] + 1; 36 anc[v][0] = u; 37 len[v] = e[i].v; 38 dfs(v, u); 39 } 40 } 41 void LCA_init(int n) 42 { 43 for(int j = 1; (1 << j) < n; j++) 44 for(int i = 1; i <= n; i++) if(anc[i][j-1]) 45 anc[i][j] = anc[anc[i][j-1]][j-1]; 46 } 47 int LCA(int u, int v) 48 { 49 int log; 50 if(dep[u] < dep[v]) swap(u, v); 51 for(log = 0; (1 << log) < dep[u]; log++); 52 for(int i = log; i >= 0; i--) 53 if(dep[u] - (1 << i) >= dep[v]) u = anc[u][i]; 54 if(u == v) return u; 55 for(int i = log; i >= 0; i--) 56 if(anc[u][i] && anc[u][i] != anc[v][i]) 57 u = anc[u][i], v = anc[v][i]; 58 return anc[u][0]; 59 } 60 int fa[maxn]; 61 int Find(int x) 62 { 63 if(x == fa[x]) return x; 64 return fa[x] = Find(fa[x]); 65 } 66 int main() 67 { 68 int n, m; scanf("%d %d", &n, &m); 69 cnt = 1; 70 for(int i = 1; i <= n; i++) h[i] = 0; 71 for(int i = 1; i <= n - 1; i++) 72 { 73 int u, v; 74 ll w; scanf("%d %d %lld", &u, &v, &w); 75 add(u, v, w), add(v, u, w); 76 } 77 ///LCA初始化 78 dfs(1, 0); 79 LCA_init(n); 80 ///并查集初始化 81 for(int i = 1; i <= n; i++) fa[i] = i; 82 while(m--) 83 { 84 int op, a, b, p; 85 ll c, y; 86 scanf("%d", &op); 87 if(op == 1) 88 { 89 scanf("%d %d %lld", &a, &b, &y); 90 int fp = LCA(a, b); 91 a = Find(a); 92 while(dep[a] > dep[fp] && y > 0LL) 93 { 94 if(len[a] == 1LL) 95 { 96 fa[a] = anc[a][0]; 97 a = Find(a); 98 } 99 else 100 { 101 y /= len[a]; 102 a = Find(anc[a][0]); 103 } 104 } 105 b = Find(b); 106 while(dep[b] > dep[fp] && y > 0LL) 107 { 108 if(len[b] == 1LL) 109 { 110 fa[b] = anc[b][0]; 111 b = Find(b); 112 } 113 else 114 { 115 y /= len[b]; 116 b = Find(anc[b][0]); 117 } 118 } 119 printf("%lld\n", y); 120 } 121 else 122 { 123 scanf("%d %lld", &p, &c); 124 int u = e[p * 2].to, v = e[(p * 2) ^ 1].to; 125 if(u == anc[v][0]) 126 { 127 len[v] = c; 128 if(c == 1LL) 129 { 130 fa[v] = u; 131 } 132 } 133 else 134 { 135 len[u] = c; 136 if(c == 1LL) 137 { 138 fa[u] = v; 139 } 140 } 141 } 142 } 143 return 0; 144 }
