第一次博客作业--线性表

0.PTA得分截图#

1.本周学习总结（0-4分）#

1.1 总结线性表内容##

  • 顺序表结构体定义
typedef struct
{
	ElemType data[MaxSize];		//存放顺序表元素
	int length;			//存放顺序表的长度
} List;
typedef List* SqList;
  • 顺序表插入和删除
void InsertSq(SqList& L, int x)//顺序表插入
{
	int i, j;
	for (i = 0; i < L->length; i++)
	{
		if (L->data[i] > x)
		{
			for (j = L->length; j > i; j--)
			{
				L->data[j] = L->data[j - 1];
			}
			L->data[i] = x;
			L->length++;
			break;
		}
	}
	if (i == L->length)
	{
		L->data[i] = x;
		L->length++;
	}
}
void DelSameNode(List& L)//顺序表删除相同元素
{
	int i, j, k;
	for (i = 0; i < L->length; i++)
	{
		j = i + 1;
		for (; j <= L->length; j++)
		{
			if (L->data[i] == L->data[j])
			{
				for (k = j; k < L->length - 1; k++)
				{
					L->data[k] = L->data[k + 1];
				}
				L->length--;
			}
			
		}
	}
}
  • 链表结构体定义
typedef struct LNode  		//定义单链表结点类型
{
	ElemType data;
	struct LNode* next;		//指向后继结点
} LNode, * LinkList;
  • 链表头插法、尾插法、有序链表插入、删除
void CreateListF(LinkList& L, int n)//头插法建链表
{
	LinkList newptr;
	LinkList oldptr;
	LinkList nowptr;
	int i;
	L = new LNode;
	L->next = NULL;
	oldptr = L;
	newptr = L->next;

	for (i = 1; i <= n; i++)
	{
		nowptr = new LNode;
		cin >> nowptr->data;
		nowptr->next = oldptr->next;
		oldptr->next = nowptr;
		newptr = nowptr;
	}

}
void CreateListR(LinkList& L, int n)//尾插法建带头结点链表
{
	LinkList node, tail;
	int i;
	L = new LNode;
	L->next = NULL;
	tail = L;
	for (i = 1; i <= n; i++)
	{
		node = new LNode;
		cin >> node->data;
		tail->next = node;
		tail = node;
	}
	tail->next = NULL;
}
void ListInsert(LinkList& L, ElemType e)//链表插入元素
{
	LinkList pre, ptr;
	LinkList p;
	p = new LNode;
	p->data = e;
	pre = L->next;

	while (pre->next)
	{
		if (pre->next->data > e)
		{
			p->next = pre->next;
			pre->next = p;
			break;
		}
		else
		{
			pre = pre->next;
		}
	}
	if (pre->next == NULL)
	{
		p->next = pre->next;
		pre->next = p;
	}
}
void ListDelete(LinkList& L, ElemType e)//链表删除元素
{
	LinkList pre, ptr;
	pre = L;
	int flag = 1;
	if (L->next == NULL)
	{
		return;
	}
	while (pre->next)
	{
		if (pre->next->data == e)
		{
			ptr = pre->next;
			pre->next = pre->next->next;
			delete ptr;
			flag = 0;
			break;
		}
		else
		{
			pre = pre->next;
		}
	}
        if (flag==1)
	{
		cout << e << "找不到！" << endl;
	}
}
  • 有序表合并
void MergeList(LinkList& L1, LinkList L2)//合并链表
{
	LinkList p1, p2, p3 = L1;
	p1 = L1->next;
	p2 = L2->next;
	L1->next = NULL;

	while (p1 && p2)
	{
		if (p1->data < p2->data)
		{
			p3->next = p1;
			p3 = p1;
			p1 = p1->next;
		}
		else if (p1->data > p2->data)
		{
			p3->next = p2;
			p3 = p2;
			p2 = p2->next;
		}
		else
		{
			p3->next = p1;
			p3 = p1;
			p1 = p1->next;
			p2 = p2->next;
		}
	}
	if (p1 != NULL)
	{
		p3->next = p1;
	}
	if (p2 != NULL)
	{
		p3->next = p2;
	}
}
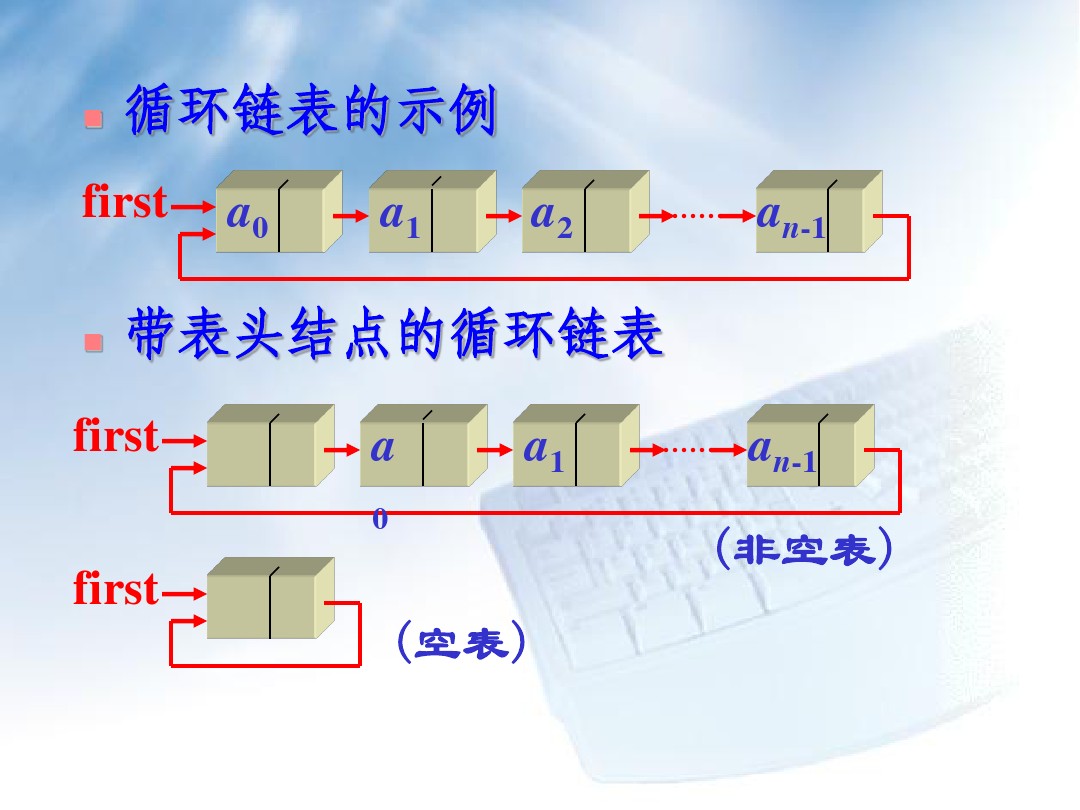
  • 循环链表、双链表结构特点
    • 循环链表是单链表的变形，循环链表最后一个结点的指针不为NULL，而是指向了表的前端，为简化操作，在循环链表中往往加入表头结点，循环链表的特点是：只要知道表中某一结点的地址，就可搜寻到所有其他结点的地址。
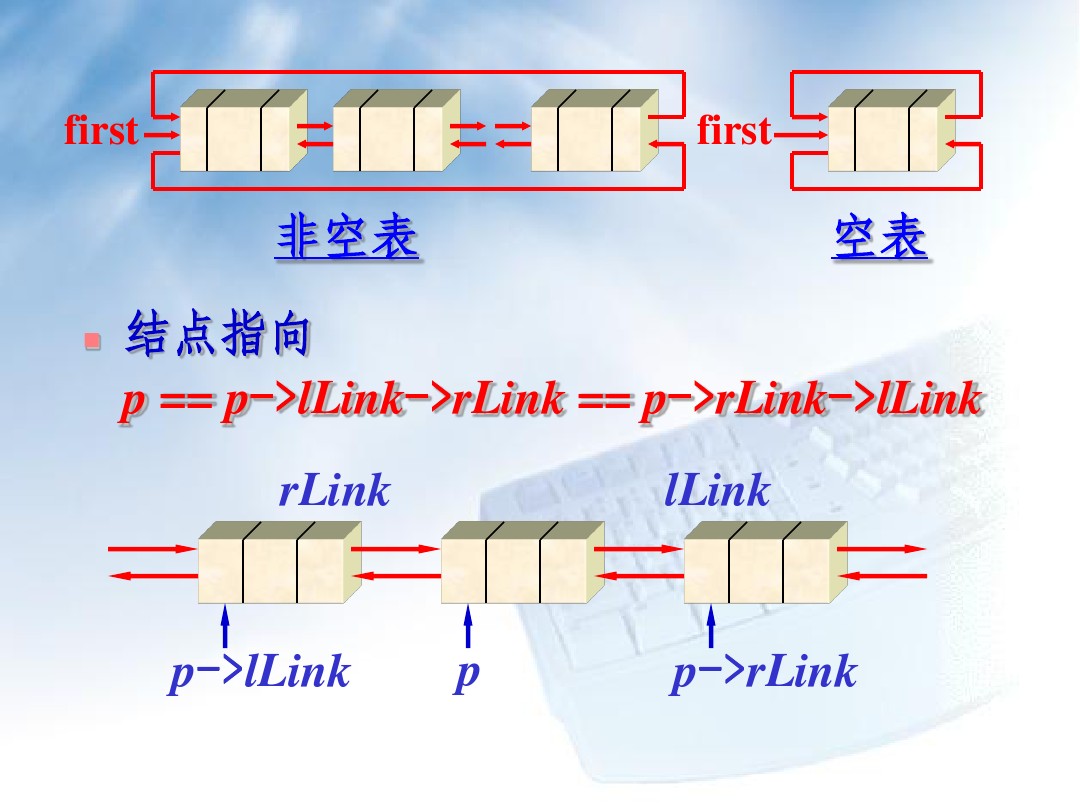
    • 双链表有两个特点：一是可以从两个方向搜索某个结点，这使得链表的某些操作（如插入和删除）变得比较简单； 二是无论利用前链还是后链都可以遍历整个双向链表。

1.2.谈谈你对线性表的认识及学习体会。##

  • 线性表有两种方式:
    1.顺序线性表 (也就是用数组实现的,在内存中有顺序排列,通过改变数组大小实现)
    2.链表 (不是用顺序实现的,用指针实现,在内存中不连续！)
    顺序线性表的缺点：1.插入和删除操作需要移动大量的元素。在顺序表上插入和删除平均要移动一半的元素。2.表的容量难以确定。因为数组的长度要提前声明。3.数组要求占用连续的存储空间，即使存储单元数超过所需要的数目，如果不连续也不能用。而链式存储就没有这种缺点，每一个结点都是程序员自己向计算机申请的，如果不需要的话就会释放掉，将内存返还给系统，而且表的容量是确定的，各个节点的存储地址是不连续的，各个节点通过自己的数据域存储信息，通过指针域来存储下一个结点的信息。但如果一个结点的指针域数据丢失了，那他的下一个结点就找不到了。
       单链表的构建有头插和尾插两种方法，无论是哪一种方法都需要从空表的构建开始。头插法就是新插入的每一个结点都在头节点之后，最先插入的节点变为尾节点，而尾插法是每个插入的结点都是插在链表的最后，作为尾节点出现的。这里代码就不给出。课本上都有，在链表构建好之后就可以进行一系列的操作。比如查找删除插入遍历等等。。。
    如果希望除了可以确定一个结点的后继外，还可以找到它的前驱，那么我们就可以构建双链表，就是在单链表的每个结点中在设置一个指向其前驱结点的指针域。和单链表类似，它一般也是由头指针唯一确定。
    对于单链表，每个结点只存储了向后的指针，到了尾结点就停止了向后的操作。我们将单链表中终端结点的指针端由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表，简称循环链表。 循环链表和单链表的主要差异在于循环的判断条件上，之前是判断temp->next是否为空，现在是temp->next不等于头结点，.循环链表最后一个结点的 link 指针不 为NULL，而是指向了表的前端。 它只要知道表中某一结点的地址，就可搜寻到所有其他结点的地址。

2.PTA实验作业（0-2分）#

2.1.题目1：6-10 jmu-ds-有序链表的插入删除##

2.1.1代码截图###



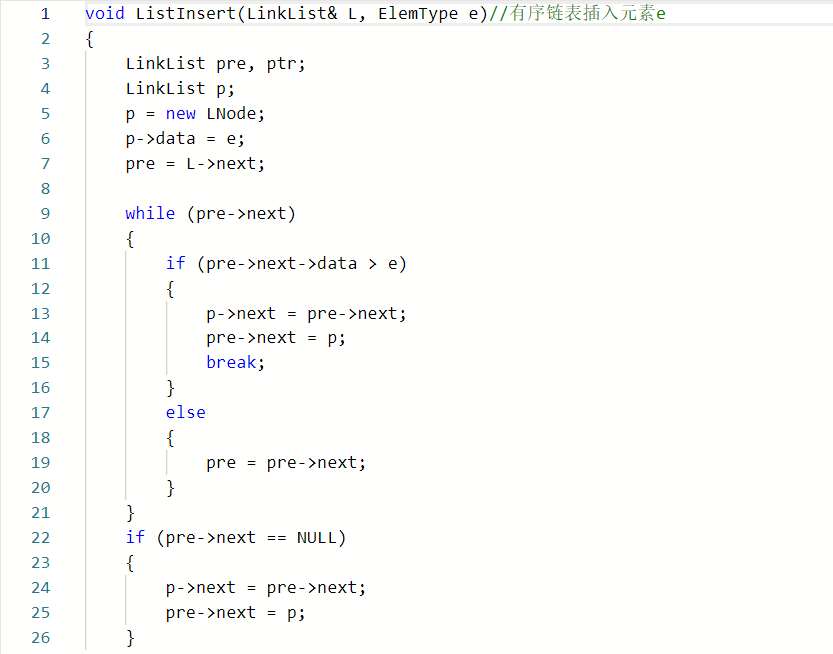
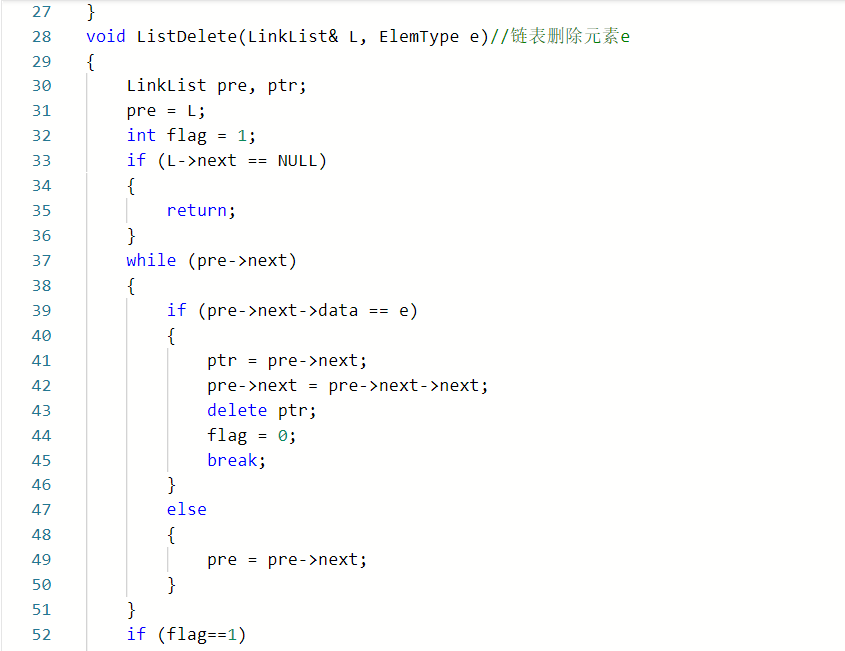
2.1.2本题PTA提交列表说明。###

Q：全部删除出现错误
A：增加了一个链表为空时的附加条件，让其及时返回
Q：增加的条件出现错误
A：把=改成==就对了

**2.2.题目2：6-11 jmu-ds-链表分割 **##

2.2.1代码截图###


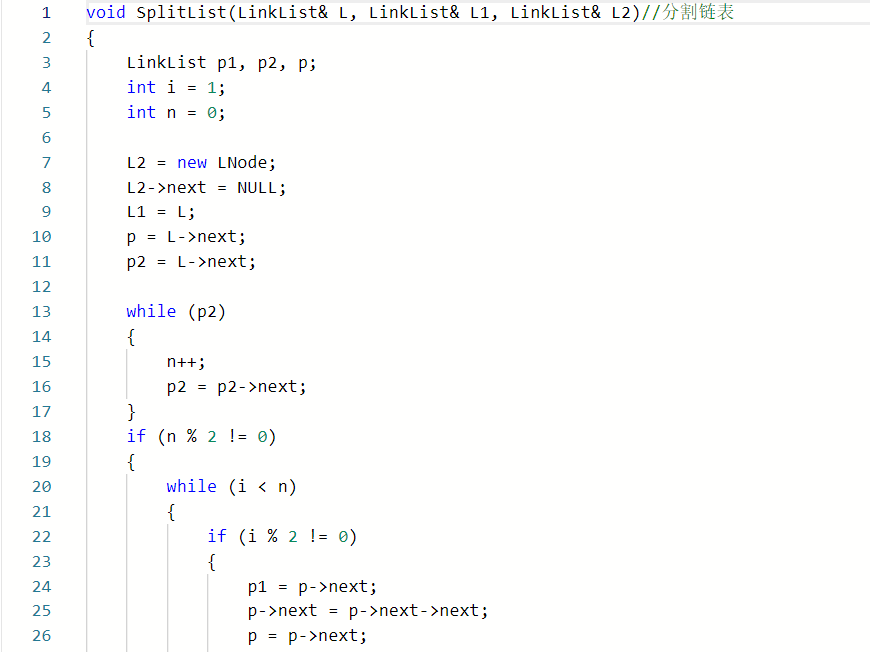
2.2.2本题PTA提交列表说明。###

Q：分割得到的第二条链表输出不完整
A：修改了循环结束的条件，晚一点结束循环
Q：链表长度为偶数时输出正确，为奇数时输出错误
A：为偶数和奇数分别设置不同的条件

**2.3.题目1：6-8 jmu-ds-链表倒数第m个数 **##

2.3.1代码截图###

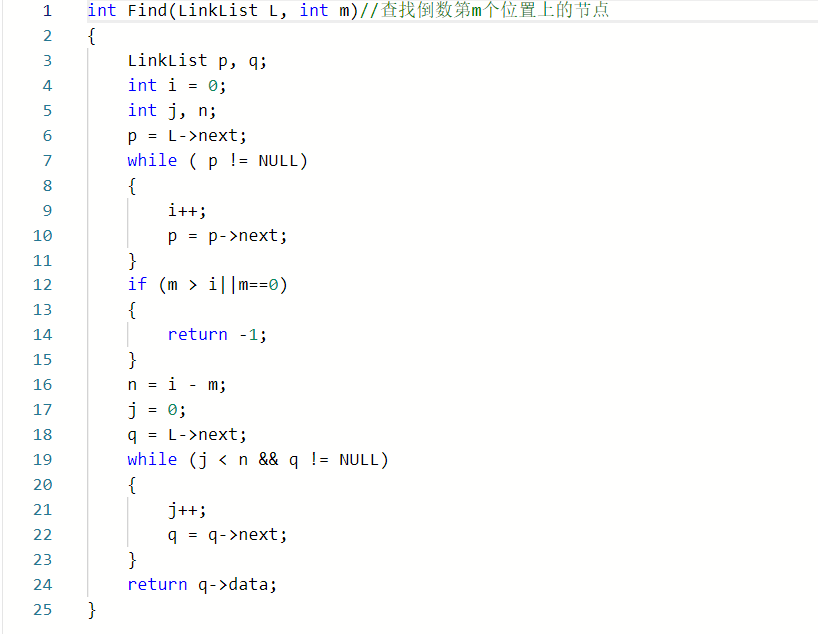
2.3.2本题PTA提交列表说明。###

Q：没有考虑无效位置
A：增加了一个条件判断无效位置
Q：出现了段错误，少考虑一个特殊的无效位置
A：把m=0这个特殊的无效位置考虑进去就对了

3.阅读代码（0--4分）#

3.1 题目及解题代码##

对链表进行插入排序

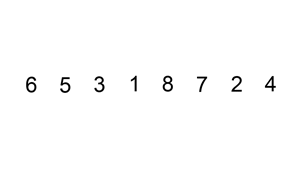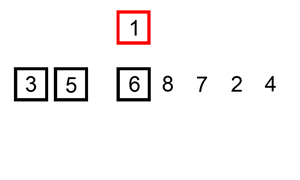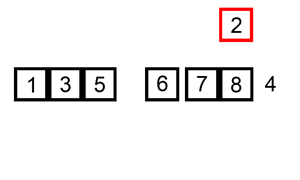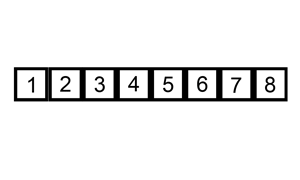
插入排序的动画演示如上。从第一个元素开始，该链表可以被认为已经部分排序（用黑色表示）。
每次迭代时，从输入数据中移除一个元素（用红色表示），并原地将其插入到已排好序的链表中。
插入排序算法：
插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
重复直到所有输入数据插入完为止。
示例 1：
输入: 4->2->1->3
输出: 1->2->3->4
示例 2：
输入: -1->5->3->4->0
输出: -1->0->3->4->5

ListNode* insertionSortList(ListNode* head) {
        if (!head) return head;
        ListNode *dummyHead = new ListNode(0); 
        ListNode *pre = dummyHead;
        ListNode *current = head;
        ListNode *next = nullptr;
        while (current) {
            next = current->next; 
            while (pre->next != nullptr && pre->next->val < current->val) {
                pre = pre->next;
            }
            current->next = pre->next; 
            pre->next = current; 
            pre = dummyHead; 
            current = next; 
        }
        return dummyHead->next;
    }

3.1.1 该题的设计思路###

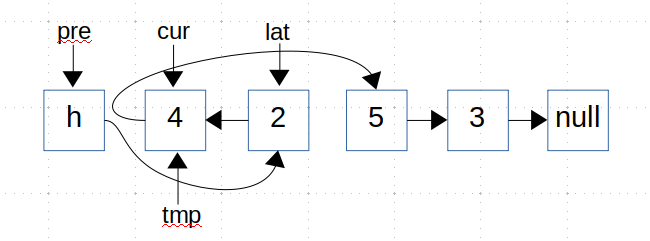
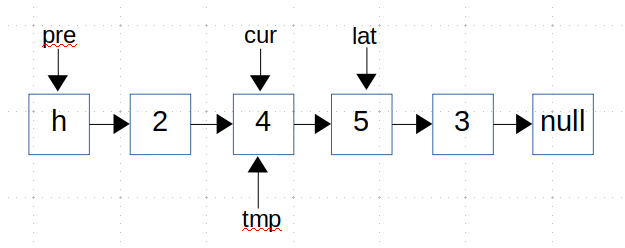
  • 因为有insert操作，所有我们上来就定义三个指针pre、cur、lat。我们首先考虑2应该插在哪？
  • 我们发现2比tmp小，所以我们需要将2插入到tmp前。
  • 我们主要实现的操作就是
  • 接着我们需要将pre和tmp复位，同时我们需要移动cur和lat找到下一个需要被插入元素的位置。

    时间复杂度为O(n^2),空间复杂度为O(1)

3.1.2 该题的伪代码###

       判断是否为空
        ListNode *dummyHead = new ListNode(0); //来一个虚拟头结点作为有序链表的头结点
        ListNode *pre = dummyHead;
        ListNode *current = head;
        ListNode *next = nullptr;
        while (current) {
            next记录下一个位置
            while (pre->next != nullptr && pre->next->val < current->val) {
                pre = pre->next; //pre->next 位置就是需要插入元素的位置
            }
            end while
            把比current大的节点接到current后面
            将current接到合适的位置
            重置指针
            current = next; //接着比较下一个
        }
        end while
        return dummyHead->next;
    }

3.1.3 运行结果###

3.1.4分析该题目解题优势及难点。###

  • 优势：它巧妙的为新链表建了一个虚拟头结点dummyHead，dummyHead->next就是需要返回的链表。
  • 难点：由于是插入排序，存在一种可能使得最小的元素处于原链表中间甚至是末尾位置，此时对于新链表而言其头结点就会发生变化。

3.2 题目及解题代码##

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。
k 是一个正整数，它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。
示例：
给你这个链表：1->2->3->4->5
当 k = 2 时，应当返回: 2->1->4->3->5
当 k = 3 时，应当返回: 3->2->1->4->5

public ListNode reverseKGroup(ListNode head, int k) {
    if (head == null || head.next == null || k <= 1) {
        return head;
    }
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    ListNode pointer = dummy;

    while (pointer != null) {
        ListNode lastGroup = pointer;

        int i = 0;            
        for (; i < k; ++i) {
            pointer = pointer.next;
            if (pointer == null) {
                break;
            }
        }

        if (i == k) {
            ListNode nextGroup = pointer.next;
            ListNode reversedList = reverse(lastGroup.next, nextGroup);
            pointer = lastGroup.next;
            lastGroup.next = reversedList;
            pointer.next = nextGroup;
        }
    }
    return dummy.next;
}
private ListNode reverse(ListNode head, ListNode tail) {
    if (head == null || head.next == null) {
        return head;
    }
    ListNode prev = null, temp = null;
    while ((head != null) && (head != tail)) {
        temp = head.next;
        head.next = prev;
        prev = head;
        head = temp;
    }

    return prev;
}

3.2.1 该题的设计思路###


时间复杂度为O(n*k),空间复杂度为O(1)。

3.2.2 该题的伪代码###

public ListNode reverseKGroup(ListNode head, int k) {
    判断是否为空
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    ListNode pointer = dummy;

    while (pointer != null) {
        记录上一个子链表的尾
        int i = 0;            
        for (; i < k; ++i) {
            pointer = pointer.next;
            若为空，结束循环
        }
        end for
        如果当前子链表的节点数满足 k, 就进行反转
        反之，说明程序到尾了，节点数不够，不用反转
        if (i == k) {
            记录下一个子链表的头
            反转当前子链表，reverse 函数返回反转后子链表的头
            lastGroup 是上一个子链表的尾，其 next 指向当前反转子链表的头
            但是因为当前链表已经被反转，所以它指向的是反转后的链表的尾
            pointer = lastGroup.next;
            将上一个链表的尾连向反转后链表的头
            lastGroup.next = reversedList;
            当前反转后的链表的尾连向下一个子链表的头
            pointer.next = nextGroup;
        }
        end if
    }
    end while
    return dummy.next;
}
private ListNode reverse(ListNode head, ListNode tail) {
    判断是否为空
    ListNode prev 和temp 赋为空
    while ((head != null) && (head != tail)) {
        进行反转
    }
    end while
    return prev;
}

3.2.3 运行结果###

3.2.4分析该题目解题优势及难点。###

  • 优势：把一个很长的链表分成很多个小链表，每一份的长度都是 k (最后一份的长度如果小于 k 则不需要反转)，然后对每个小链表进行反转，最后将所有反转后的小链表按之前的顺序拼接在一起。在反转子链表的时候，上一个子链表的尾知道。下一个子链表的头也知道。当前反转的链表的头尾都知道。
  • 难点：其实链表的题目并不需要特别强的逻辑推理，它主要强调细节实现，难也是难在细节实现上面 ，虽然大致的方向知道，但是很可能写着写着就会乱。一般赋值的时候需要新建一个临时节点，可以存储即将移到最前端的那个节点，然后按照位置由后到前的顺序为各个变量的next赋值，写完要检查一下，某个下一行作为右值的变量，在上一行它的next是否被改变了？如果被改变了就要警惕，这可能不是正常的赋值顺序。

posted on 2020-03-08 22:27  王威。  阅读(257)  评论(2)  编辑  收藏  举报

导航