2024-2025-1 20241404《计算机基础与程序设计》第一周学习总结
| 这个作业属于哪个课程 | 2024-2025-1-计算机基础与程序设计 |
|---|---|
| 这个作业要求在哪里 | [2024-2025-1计算机基础与程序设计第一周作业]https://www.cnblogs.com/wangsiwen666/p/18439419 |
| 这个作业的目标 | 作业具体目标是让我们能够培养自主思考能力,以及对教材的更深一步的理解,还能够让我们在实践中锻炼能力,做到在实践中学习。 |
| 正文: |
一、## 教材学习内容总结
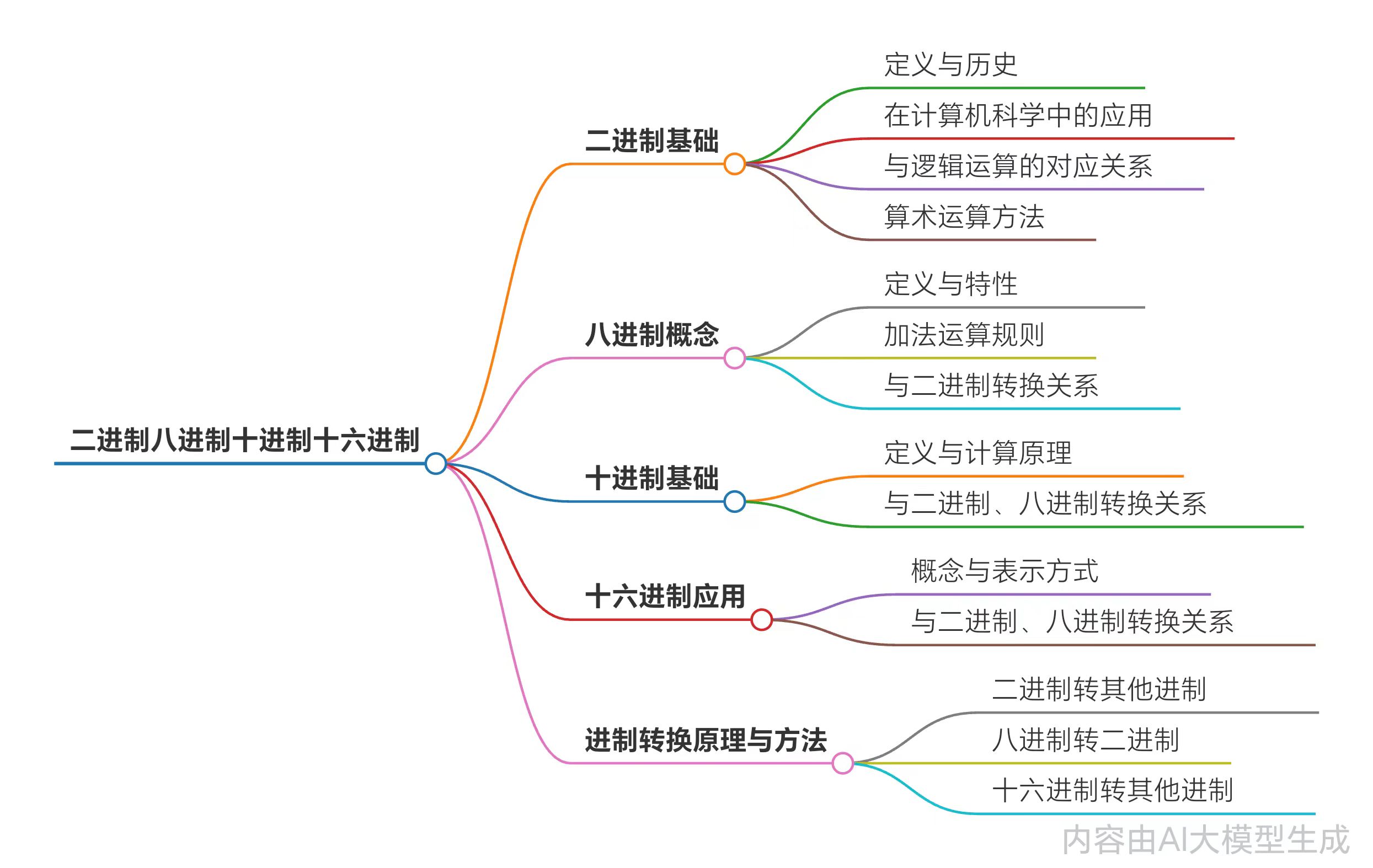
- 二进制
二进制是一种基数为2的数制,只使用0和1两个数字。在计算机科学中,二进制是最基础的数制,因为计算机内部的所有数据都是以二进制形式存储和处理的。例如,计算机使用二进制来表示逻辑状态(开/关),即0表示关,1表示开。 - 八进制
八进制是一种基数为8的数制,使用0到7八个数字。八进制在计算机科学中也有一定的应用,尤其是在表示字节和其他二进制数的组合时。例如,一个八进制数可以表示为三个二进制数的组合。 - 十进制
十进制是我们日常生活中最常用的数制,基数为10,使用0到9十个数字。十进制在计算机科学中用于表示和处理各种数值数据。例如,计算机中的算术运算和数据存储通常都基于十进制。 - 十六进制
十六进制是一种基数为16的数制,使用0到9和A到F十六个符号。十六进制在计算机科学中非常常见,尤其是在表示内存地址、颜色代码和某些编程语言中的数据类型时。例如,一个十六进制数可以表示为四个二进制数的组合。
5、这些数制之间的转换方法如下:
二进制转八进制:将每3个二进制数分为一组(从左至右),不够时补0,然后将每组二进制数转换为对应的八进制数。
二进制转十六进制:将每4个二进制数分为一组(从左至右),不够时补0,然后将每组二进制数转换为对应的十六进制数。
八进制转二进制:将每个八进制数转换为对应的3位二进制数。
十六进制转二进制:将每个十六进制数转换为对应的4位二进制数。
通过这些转换方法,可以在不同的数制之间进行灵活的转换,从而更好地理解和处理计算机中的数据。
![]()
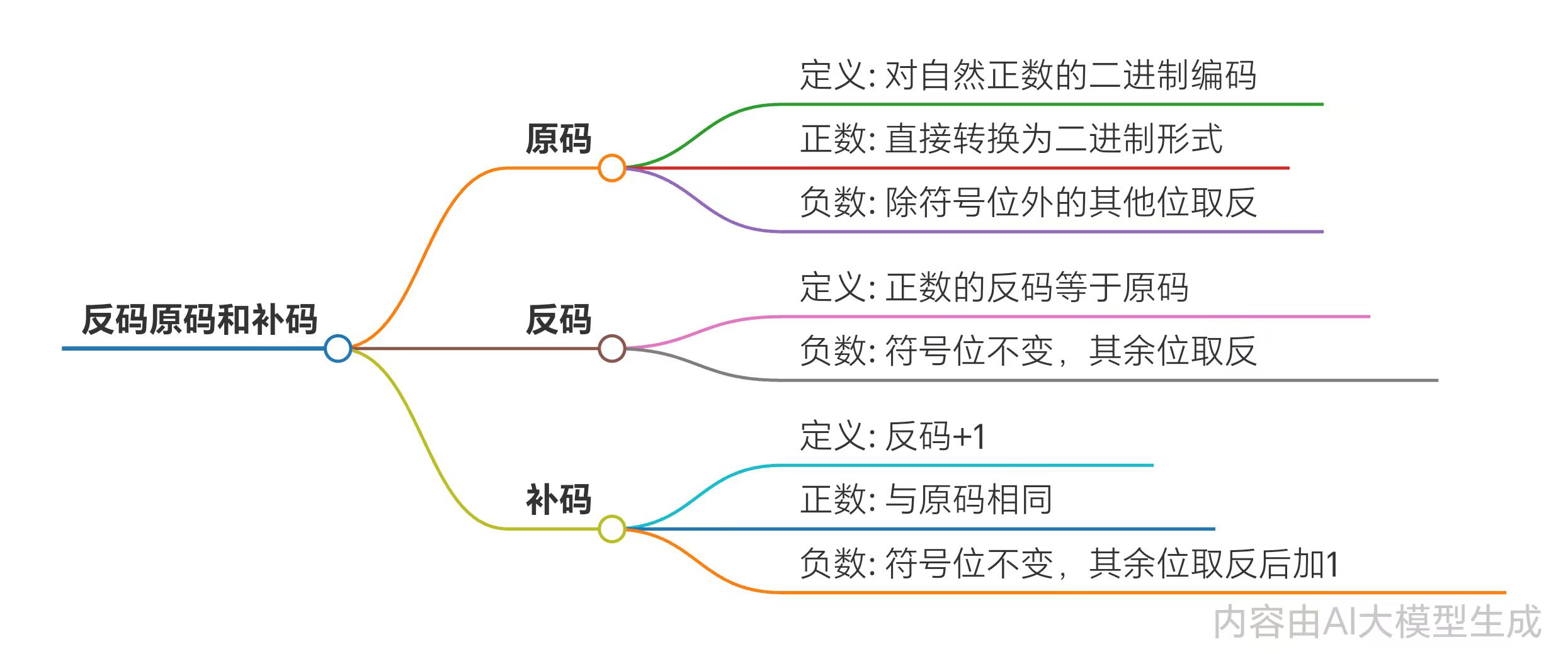
二、原码、反码和补码是计算机中表示有符号整数的三种编码方式。它们的主要目的是为了简化计算机中的算术运算,尤其是二进制数的加减运算。 - 原码:
原码是最直观的表示方法,直接将数值按照正负数的形式翻译成二进制。
最高位(最左边的位)是符号位,0表示正数,1表示负数。
其余位表示数值本身。
例如,十进制数 +5 的原码表示为 0000 0101,而 -5 的原码表示为 1000 0101。 - 反码:
反码主要用于表示负数。
对于正数,其反码与其原码相同。
对于负数,其反码是将原码除符号位外的所有位取反(0 变 1,1 变 0)。
例如,十进制数-5的反码表示为 1111 1010。 - 补码:
补码是计算机中最常用的表示方法,用于进行二进制加法运算。
对于正数,其补码与其原码相同。
对于负数,其补码是在其原码的基础上,符号位不变,其余各位取反后加1(即在反码的基础上加1)。
例如,十进制数-5的补码表示为 1111 1011。
总结:
1、正数的原码、反码和补码均为其本身。
2、负数的原码、反码和补码的转换关系如下:
原码:符号位为1,其余位为数值的二进制表示。
反码:符号位不变,其余位取反。
补码:符号位不变,其余位取反后加1
![]()
![]()
教材学习中的问题和解决过程
1.问:能够一眼看出八进制小数对应的二进制值或者看出二进制小数对应的八进制值吗?
答:不能。
虽然可以通过一些方法将八进制和二进制进行转换,但通常情况下,我们不能直接通过简单的观察来确定八进制小数对应的二进制值或二进制小数对应的八进制值。这是因为八进制和二进制之间的转换涉及到特定的规则和步骤,而不是简单的对应关系。
例如,八进制数转换为二进制数时,通常需要将每个八进制数字转换为三位二进制数,然后将这些二进制数组合起来。同样,二进制数转换为八进制数时,也需要将每三位二进制数转换为一个八进制数字。这些转换过程需要遵循特定的规则和步骤,而不是通过简单的观察就能完成的。
因此,虽然有一些在线工具和方法可以帮助我们快速进行这种转换,但直接通过观察来确定转换结果是不可能的。
2.我看了这一段文字:要在计算机上存储二进制的浮点数,可以保存定义它的三个值。例如,根据一条通用规则,如果64位存储一个浮点值,那么其中1位存储符号,11位存储指数,52位存储尾数。有这个问题:十进制小数如何转化为二进制浮点值
解答:如123.456
将十进制数123.456转换为二进制的过程可以分为整数部分和小数部分的转换。
一、 整数部分(123)的转换
除2取余法
将整数部分123进行转化为
1111011。
二、 小数部分(0.456)的转换
- 乘2取整法:将0.456不断乘以2,记录每次的整数部分,直到小数部分为0或达到所需精度。
- 0.456 × 2 = 0.912 取整数部分 0
- 0.912 × 2 = 1.824 取整数部分 1
- 0.824 × 2 = 1.648 取整数部分 1
- 0.648 × 2 = 1.296 取整数部分 1
- 0.296 × 2 = 0.592 取整数部分 0
- 0.592 × 2 = 1.184 取整数部分 1
- 0.184 × 2 = 0.368 取整数部分 0
- 0.368 × 2 = 0.736 取整数部分 0
- 0.736 × 2 = 1.472 取整数部分 1
- 0.472 × 2 = 0.944 取整数部分 0
- 排列整数部分:将所有整数部分从上往下排列,得到二进制表示为:0.01110100101111001。
合并整数和小数部分
将整数部分和小数部分合并,得到最终的二进制表示为:1111011.01110100101111001。
|第一章|洋葱模型中内层与外层有何种联系|
|第二章|二进制中的加减乘除法则是否与十进制中相同|
|第三章|索引颜色是否可以通过增加图像可使用的颜色数来增加文件大小|
|第四章|各种门有什么区别 |
| 第五章 |不同的总线宽度同时能传输的位数|
| 第六章|虚拟机能干什么|
|第七章|二分检索与顺序搜索算法内容差异是什么
第八章:算法中抽象数据类型的容量如何计算
第九章:编译器与解释器的相同点
第十章:;逻辑地址与物理地址的区别
第十一章:目录树绝对途径与相对途径的区别
第十二章:电子数据表循环应用如何操作
第十三章:数据库的模式是什么
第十四章:为什么动态的、交互式的和复杂的系统适合模拟
第十五章:网络地址的作用
第十六章:cookie为什么没有被广泛接受
第十七章:信息安全的CIA是什么
第十八章:误差校正码如何运作
基于AI的学习
1.AI问:补码相对于原码的好处
答:补码相对于原码和反码的主要好处在于它简化了计算机中的数学运算,特别是在进行加减运算时。补码的出现解决了原码和反码在表示负数时的一些问题,并且使得计算机可以正确地表示和处理负数。
2AI问:二进制有哪些局限性?
回答:二进制的主要局限性在于其表示能力有限,尤其是在处理大数值时,需要更多的位数来表示。此外,二进制在表示负数时需要额外的符号位或补码表示法。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号