后缀数组学习笔记
1. 前置知识:基数排序
1.1. 思想
现有如下序列:3,44,38,5,47,15,36,32,50,现在要用基数排序算法排序,要怎么做?
基数排序的初始状态如下:
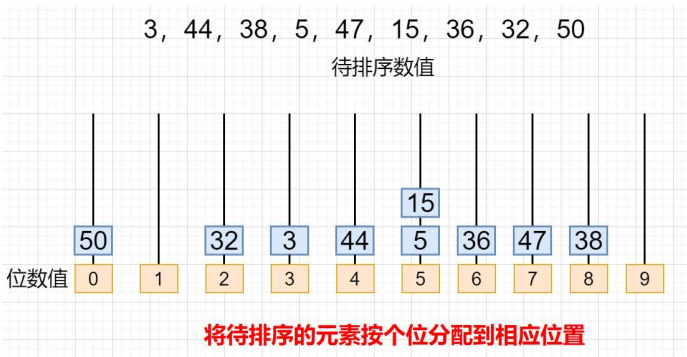
- 按照个位将原序列中的数分组,放入对应的集合
- 将分好的数按照个位的顺序取出,得到:
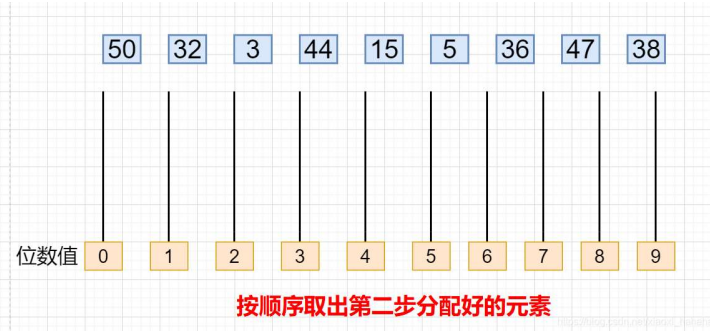
- 将序列中的数重新按照十位分组,放入对应集合:
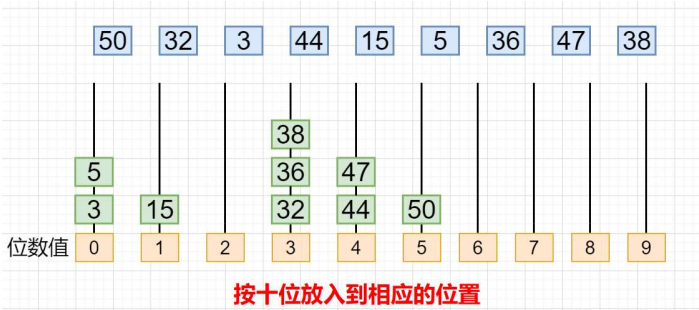
- 将每一位上的数按从下到上的顺序依次取出,就是答案
基数排序利用的是一个桶思想,属于非比较算法
在数更多或位数更多的情况下,重复此过程即可
1.2. 代码:
#include<cstdio>
#include<algorithm>
using namespace std;
int n,a[105],cnt[15],b[105];
int main()
{
scanf("%d",&n);
int mx=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
mx=max(mx,a[i]);
}
int d=0;
while(mx>0)
{
mx/=10;
d++;
}
int tmp=1;
for(int i=1;i<=d;i++)
{
for(int j=0;j<10;j++) cnt[j]=0;
for(int j=1;j<=n;j++)
{
int k=(a[j]/tmp)%10;
cnt[k]++;
}
for(int j=1;j<10;j++)
{
cnt[j]+=cnt[j-1];
}
for(int j=n;j>0;j--)
{
int k=(a[j]/tmp)%10;
b[cnt[k]]=a[j];
cnt[k]--;
}
for(int j=1;j<=n;j++)
{
a[j]=b[j];
}
tmp*=10;
}
for(int i=1;i<=n;i++)
{
printf("%d ",a[i]);
}
return 0;
}
2.基本概念
后缀:是指从某一个位置i开始直到整个串末尾的某个子串
后缀数组:用
名次数组:用
以
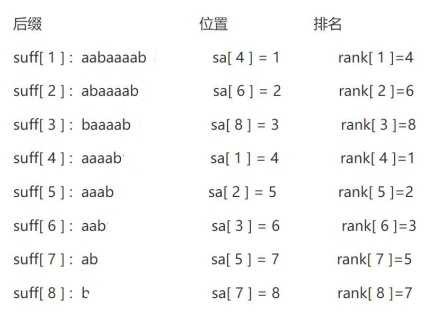
字符串的大小比较:
字符串比较是逐位按字典序比较,若字典序相同,则比较下一位,否则直接分出大小,例如:
3. 倍增求后缀数组
3.1. 思想
这里倍增比较字符串的长度
第一次是比较长度为1的字符串
第二次比较的是长度为2的字符串,可以用一个窗口
第三次比较的是长度为4的字符串,可以用一个窗口
依次类推
第
如何通过排名来比较字符串大小?
举个例子,两个长度为4的后缀str1和str2:

str1由两个长度为2的字符串拼成,他们的排名为x1和y1,str2由两个长度为2的字符串拼成,他们的排名为x2和y2
此时比较str1和str2的大小,可以以x为第一关键字,若
注意:
-
在比较的过程中,如果后续的字符不够,则用0来补足
-
当
具体比较过程如图:

这里的两个关键字,就相当于数字中的十位和个位,所以排序不分可以所以基数排序,倍增的时间复杂度为
3.2. 例题
题目背景
这是一道模板题。
题目描述
读入一个长度为
输入格式
一行一个长度为
输出格式
一行,共
样例 #1
样例输入 #1
ababa
样例输出 #1
5 3 1 4 2
提示
3.3. 代码
#include<cstdio>
#include<algorithm>
#include<string>
#include<iostream>
#include<cstring>
using namespace std;
const int N=2e6+5;
string s;
int n,x[N],y[N],cnt[N],sa[N],m;
int main()
{
cin>>s;
n=s.size();
s=" "+s;
m=122;
for(int i=1;i<=n;i++) cnt[x[i]=s[i]]++;
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=n;i>0;i--) sa[cnt[x[i]]--]=i;
for(int k=1;k<=n;k<<=1)
{
memset(cnt,0,sizeof(cnt));
for(int i=1;i<=n;i++) y[i]=sa[i];
for(int i=1;i<=n;i++) cnt[x[y[i]+k]]++;
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=n;i>0;i--) sa[cnt[x[y[i]+k]]--]=y[i];
memset(cnt,0,sizeof(cnt));
for(int i=1;i<=n;i++) y[i]=sa[i];
for(int i=1;i<=n;i++) cnt[x[y[i]]]++;
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=n;i>0;i--) sa[cnt[x[y[i]]]--]=y[i];
for(int i=1;i<=n;i++) y[i]=x[i];
m=0;
for(int i=1;i<=n;i++)
{
if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])
{
x[sa[i]]=m;
}
else x[sa[i]]=++m;
}
if(m==n) break;
}
for(int i=1;i<=n;i++)
{
printf("%d ",sa[i]);
}
return 0;
}
3.4. 后缀数组的应用
3.4.1. height数组
height数组:定义
如果按照
有一个性质:
证明:
当
当
根据
既然后缀
那么后缀
进一步地,后缀
因为后缀
于是就可以得出
所以,在求解时,就可以用着个性质,从前往后暴力匹配即可
代码:
void get_height()
{
for(int i=1;i<=n;i++) rk[sa[i]]=i;
for(int i=1,k=0;i<=n;i++)
{
if(rk[i]==1) continue;
if(k) k--;
int j=sa[rk[i]-1];
while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k]) k++;
height[rk[i]]=k;
}
}
同时,如果要求两个排名不连续的串的最长公共前缀,则直接取这段排名区间的最小值
例如aabaaaab中,求abaaaab和aaab的最长公共前缀,如图:
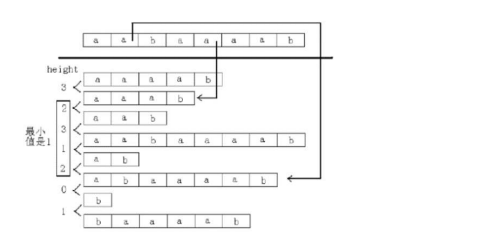
注意,最后求出来的是
3.4.2. 最长重复子串(可重叠)
显然,height所求的公共前缀必然出现了两次,所以求出所有height的最大值即可
4. 例题:
4.1. [JSOI2007] 字符加密
https://gxyzoj.com/d/gxyznoi/p/101
看到字符串排序,想后缀数组,但是如果直接排序,后面的子串就会因为不完整出现排序错误
所以,可以先将子串复制两次,然后在求sa
4.2. [luogu2408] 不同子串个数
https://gxyzoj.com/d/gxyznoi/p/102
当两个子串相等时,那么着两个子串必然是两个后缀的公共前缀
所以考虑后缀数组,排序后求出height数组,此时,如果子串s是排名相邻串的最长公共前缀,则可以直接减去长度
但是如果不相邻,则必然时其他两个相邻串的非最长公共前缀,所以在前面的统计中必然不会遗漏
4.3. [ural1297] Palindrome
https://gxyzoj.com/d/gxyznoi/p/103
从暴力开始,最简单的方法显然是枚举起点和终点,然后匹配,显然会T
考虑到,在一个回文串中,显然存在一个对称点,而将原串反转后,在原串和新串中,从对称点开始的两个后缀的公共前缀就是回文串一半(向上取整)的长度
所以可以将原串和新串拼起来,中间加一个不会出现的字符即可,记长度为n
根据上面的性质,对于中心是一个字符,求
4.4. [Poi2000] 公共串
https://gxyzoj.com/d/gxyznoi/p/P104
注意,是求所有串的公共子串!!!
在这些串中,任选各任选一个点,那么他们后缀的公共前缀就是公共子串
所以根据上面一道题,可以讲所有子串拼起来,中间用未出现的字符隔开,然后求后缀数组和height数组
接下来,因为任意两串的公共前缀是排名区间内取min,所以名次间隔越小,值就越大
可以使用双指针,当满足每一个子串都出现过时,求min即可
4.5. [USACO06DEC] Milk Patterns G
https://gxyzoj.com/d/gxyznoi/p/P105
要求的是重复出现的子串的最长长度,根据样例,是可重叠的,而且有出现次数的限制
可以借鉴3.4.2的思路,因为次数至少为k,所以当次数为x+1的答案为t时,次数为x的答案必然大于等于t
所以,可以找排名连续的k个后缀中的公共前缀的最小值,再去所有最小值的max,显然可以用单调队列
4.6. [SDOI2008] Sandy的卡片
https://gxyzoj.com/d/gxyznoi/p/P106
因为是在一个串中的一段同时加上同一个值之后,与其他串中经过同样处理后的某一部分相同
所以考虑差分,此时,相同的串在差分后必然相等,此时,这道题就变成了[Poi2000] 公共串
注意,因为比较的是差分数组,所以要加1
4.7. [Ahoi2013] 差异
https://gxyzoj.com/d/gxyznoi/p/P109
主要在于求lcp,直接for循环显然会T
因为lcp是一段数中的最小值,所以可以转换思路,由求一段的最小值变为求又多少种区间的最小值为当前数字
显然单调栈,注意,因为存在相等,所以边界要一边小于等于一边小于
4.8. [bzoj3230] 相似子串
https://gxyzoj.com/d/gxyznoi/p/P110
思路其实不难,因为是求前后的公共前缀,所以很自然的想到可以另外建一个反串,求它的sa
所以,现在的关键在于如何求出它的起始和终止位置的排名
可以记录从排名1到n的不同的前缀数的前缀和,即:
所以,可以二分解决起点问题,对于终点,因为同起点的串的排名是相邻的,而长度越短的越靠前,所以直接找到终点的起点相加即可
4.9. [NOI2015] 品酒大会
因为根据相似度的定义,就是求两个串的最长公共前缀
先考虑第一个问题
依题意得,因为当然两杯“
而公共前缀恰好是x,则要求这两个串的排名之间的最小height是x
转换思路,用height考虑,因为要求最小值,考虑将height按照从大到小的顺序排序,然后依次加入
当加入一个height后,必然会将两个区域连接起来,而所有在左右各选一个点所构成的区间,最小值必然是当前值
这时只需要将左右的个数乘起来即可,因为涉及区间的合并,可以采用并查集
接下来考虑第二个问题
显然是在左和右各选一个点的值相乘,但是因为存在负数,所以还要记录最小值



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律