Educational Codeforces Round 54 (Rated for Div. 2) D Edge Deletion (SPFA + bfs)
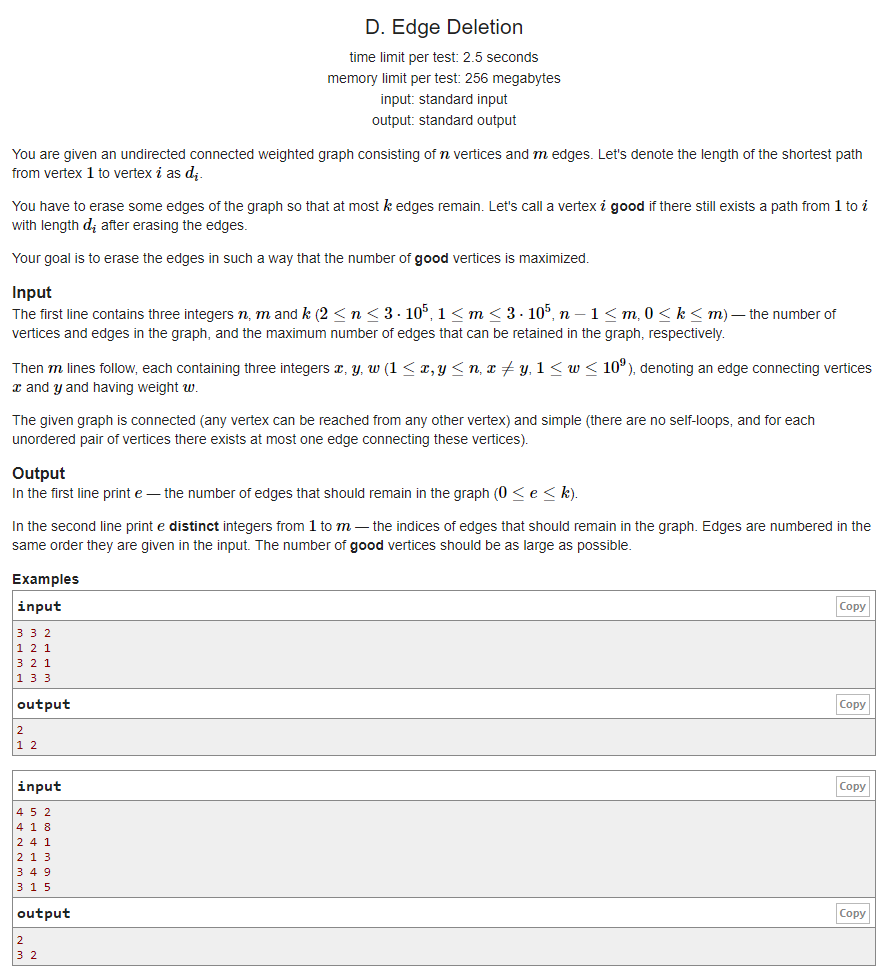
题目大意：给定你一个包含n个点m条边的无向图，现在最多在图中保留k条边，问怎么删除多的边，使得图中良好的节点数最多，求出保留在图中的边的数量和编号。
良好的节点定义为：删除某条边后该点到点1的最短距离不变。
思路：先求出所有点到点1的最短距离，之后再bfs一遍，若遍历到某一节点时的距离等于该点到点1的最短距离就将该条边加进去，直到添加到k条边或者遍历结束。（虽然过了但是还是觉得有有的情况好像过不了，但是没想出来...可能数据还有点水..）
一开始INF值设小了WA了四次。。。 INF值设置1e15即可，因为边的权值很大所以上限需要很大。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<vector> 5 #include<queue> 6 #include<map> 7 using namespace std; 8 typedef long long LL; 9 typedef pair<LL,LL> P; 10 const int maxn = 3e5+10; 11 const LL INF = 1e18; 12 vector<int>ans; 13 int n, m, k; 14 struct node{ 15 LL to,cost; 16 node() {} 17 node(LL a, LL b) :to(a), cost(b) {} 18 }; 19 vector<node> e[maxn]; 20 LL vis[maxn], f[maxn], dis[maxn]; 21 map<P,LL>mp; 22 void SPFA(int s) 23 { 24 for (int i = 0; i < maxn; i++) { 25 vis[i] = 0; f[i] = 0; 26 dis[i] = INF; 27 } 28 dis[s] = 0; 29 vis[s] = 1; f[s]++; 30 queue<int>Q; 31 Q.push(s); 32 while (!Q.empty()) { 33 int t = Q.front(); Q.pop(); 34 vis[t] = 0; 35 for (int i = 0; i < e[t].size(); i++) { 36 LL tmp = e[t][i].to; 37 if (dis[tmp] > dis[t] + e[t][i].cost) { 38 dis[tmp] = dis[t] + e[t][i].cost; 39 if (!vis[tmp]) { 40 vis[tmp] = 1; 41 Q.push(tmp); 42 if (++f[tmp] > n)return; 43 } 44 } 45 } 46 } 47 return; 48 } 49 void BFS(LL x) 50 { 51 ans.clear(); 52 queue<node>Q; 53 memset(vis,0,sizeof(vis)); 54 Q.push(node(x,0)); 55 vis[x] = 1; 56 while(!Q.empty()&&ans.size()<k){ 57 node dep = Q.front();Q.pop(); 58 for(int i=0;i<e[dep.to].size();i++){ 59 LL to = e[dep.to][i].to; 60 if(ans.size()>n-1&&ans.size()<k){ 61 ans.push_back(mp[make_pair(dep.to,to)]); 62 continue; 63 } 64 if(ans.size()==k)return; 65 if(vis[to])continue; 66 if((dep.cost+e[dep.to][i].cost)>dis[to])continue; 67 ans.push_back(mp[make_pair(dep.to,to)]); 68 vis[to] = 1; 69 Q.push(node(to,dep.cost+e[dep.to][i].cost)); 70 if(ans.size()==k)return; 71 } 72 } 73 } 74 int main() 75 { 76 ios::sync_with_stdio(false); 77 while (cin >> n >> m >> k) { 78 mp.clear(); 79 for(int i=1;i<=n;i++)e[i].clear(); 80 for (LL a, b, c, i = 1; i <= m; i++) { 81 cin >> a >> b >> c; 82 e[a].push_back(node(b, c)); 83 e[b].push_back(node(a, c)); 84 mp[make_pair(a,b)] = i; 85 mp[make_pair(b,a)] = i; 86 // cout<<mp[make_pair(a,b)]<<endl; 87 } 88 if(k==0){ 89 cout<<"0"<<endl; 90 continue; 91 } 92 SPFA(1); 93 BFS(1); 94 cout<<ans.size()<<endl; 95 for(int i=0;i<ans.size()-1;i++) 96 cout<<ans[i]<<" "; 97 cout<<ans[ans.size()-1]<<endl; 98 } 99 return 0; 100 }
