51nod 1832 前序后序遍历

 

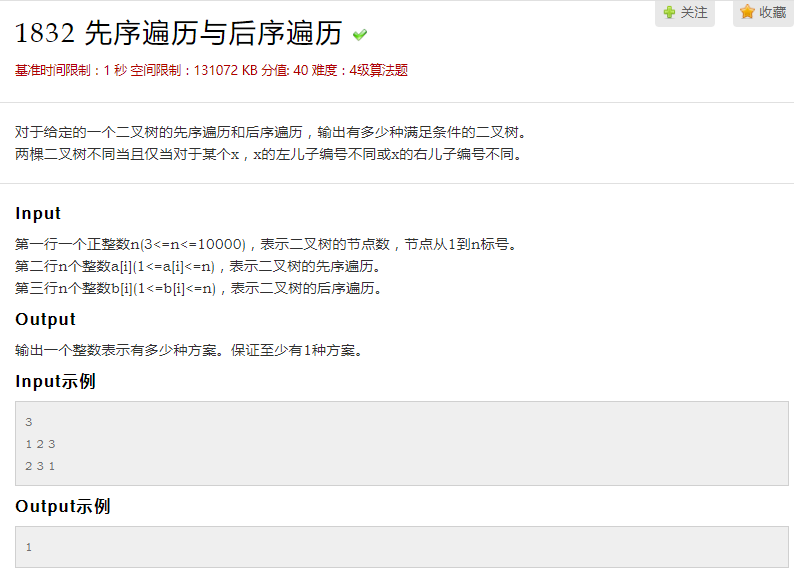
思路：设只有一颗子树的节点有ans个设前序边历数组为pre[100],后序遍历数组为pos[100]；前序遍历的第二个元素是A的一个子节点左右节点不知，设ax-ay表示一个树的前序遍历，bx-by表示后序遍历，可知如果pre[ax+1] = pos[i] 且 i = by-1,上一个根节点只有一个子树，此时令计数变量ans++；如果i ！= b2-1，很明显存在左右子树，此时应分别处理此时左子树为的前后序边历分别为：ax+1~ax+1+i-bx,bx~i,右子树为：ax+1+i-bx~ay,i+1~by-1；最后计算2^ans即为数的数目。值得注意的是：由于ans比较大，2^ans太大，需要用到大数乘法

 

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;
typedef long long LL;
const int maxn = 10005;
int n, pre[maxn], pos[maxn], ans, index[maxn];
int a[maxn * 10];
void dfs(int ax, int ay, int bx, int by)
{
    if (ax >= ay)return;
    int i = index[pre[ax + 1]];
    if (i == by - 1)ans++;
    dfs(ax + 1, ax + 1 + i - bx, bx, i);
    dfs(ax + 1 + i - bx + 1, ay, i + 1, by - 1);
}
int main()
{
    ios::sync_with_stdio(false);
    while (cin >> n) {
        ans = 0;
        for (int i = 1; i <= n; i++)cin >> pre[i];
        for (int i = 1; i <= n; i++) {
            cin >> pos[i]; index[pos[i]] = i;
        }
        dfs(1, n, 1, n);
        memset(a, 0, sizeof(a));
        a[1] = 1; n = 1;
        for (int i = 1; i <= ans; i++) {
            for (int j = 1; j <= n; j++)
                a[j] *= 2;
            for (int j = 1; j <= n; j++)
                if (a[j] >= 10) {
                    a[j + 1] = a[j + 1] + a[j] / 10;
                    a[j] %= 10;
                    n = max(n, j + 1);
                }
        }
        for (int i = n; i >= 1; i--)
            cout << a[i]; cout << endl;
    }
    return 0;
}